数学竞赛复赛试题 10页

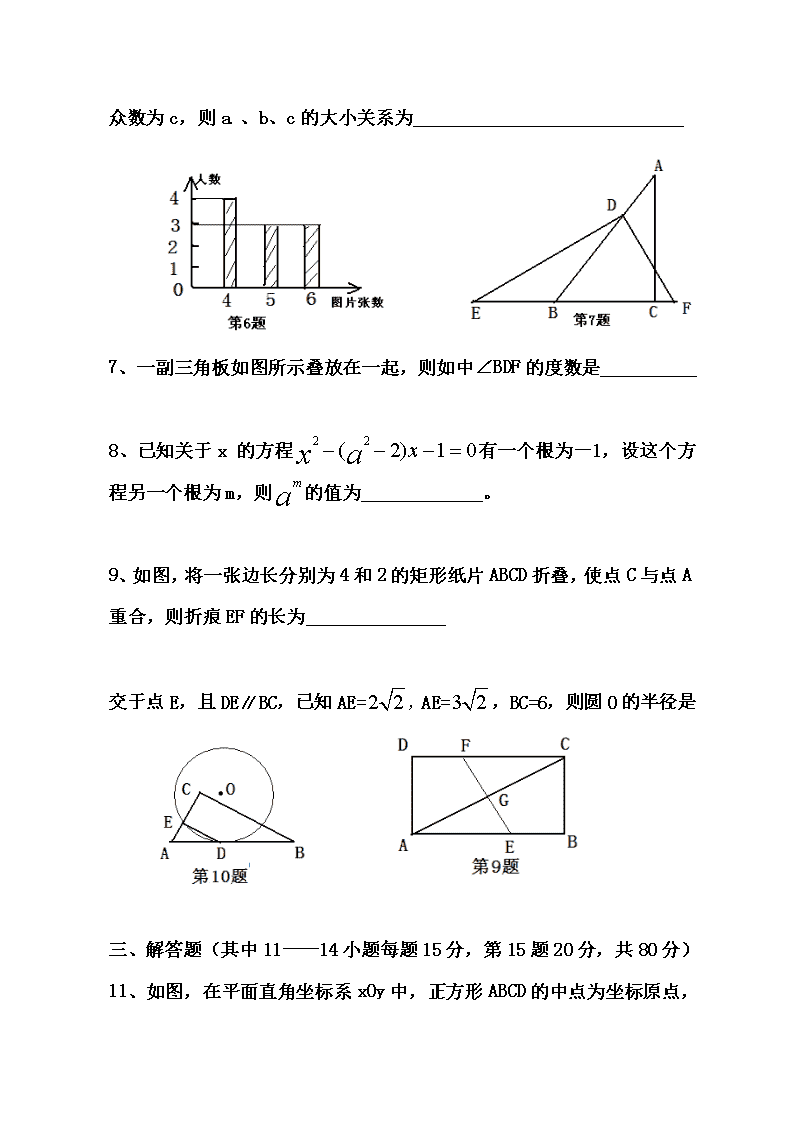
2010年全国初中数学竞赛复赛试题及参考答案（湖南）一、选择题（5×7=35）1、已知3m－1和m－7是数p的平方根，则p的值为（）A，100B，25C.10或5D.100或252、若，，则的值为（）A.BCD3、一列武广高速列车和一列普通列车的车身长分别为400米和600米，它们相向匀速行驶在平行的轨道上，若坐在高速列车上的乘客看见普通列车驶过窗口的时间是3秒，则坐在普通列车上的乘客看见高速列车驶过窗口的时间是（）A2秒B3秒C4秒D4.5秒4、如图，一个半径为3的圆O1经过一个半径为3的圆O2的圆心，则图中阴影部分的面积为（）AB9CD5、若实数a、b满足，则a的取值范围是（）Aa≤－2Ba≥4Ca≤－2或a≥4D－2≤a≤4二、填空题（5×7=35）6、若干名同学制作迎国庆卡通图片，他们制作的卡通图片张数的条形统计图如图所示，设他们制作的卡通图片张数的平均数为a\n,中位数为b，众数为c，则a、b、c的大小关系为7、一副三角板如图所示叠放在一起，则如中∠BDF的度数是8、已知关于x的方程有一个根为－1，设这个方程另一个根为m，则的值为。9、如图，将一张边长分别为4和2的矩形纸片ABCD折叠，使点C与点A重合，则折痕EF的长为交于点E，且DE∥BC，已知AE=，AE=，BC=6，则圆O的半径是三、解答题（其中11——14小题每题15分，第15题20分，共80分）\n11、如图，在平面直角坐标系xOy中，正方形ABCD的中点为坐标原点，顶点A的坐标为A（1,1），y轴上一点P（0,2）绕点A旋转180°得到点P1，点P1绕点B旋转180°得到点P2，点P2绕点C旋转180°得点P3，点P3绕点D旋转180°得点P4，……。重复操作依次得到点P1，P2，P3，……（1）、求点P1、P2、P3的坐标；（2）、求点P2010的坐标。12、一辆货车、一辆客车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶，在某一时刻，货车在前。小轿车在后，客车在货车与小轿车的中间，过了10分钟，小轿车追上了客车；又过了5分钟，小轿车追上了货车；再过t分钟，客车追上了货车，求t的值.\n13、如图，在平面直角坐标系xOY中，多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分，求直线l的函数表达式。14、如图，谢线AM,BN都垂直于线段AB，点E为AM上一点，过点A作BE的垂线AC分别交BE、BN于点F、C，过顶C作品AM的垂线CD，垂足为D。若CD=CF，求的值。15、如图，抛物线（a＞0）与双曲线相交于点A，B，已知点A的坐标为（1,4），点B在第三象限内，且△AOB的面积为3（O为原点）。（1）、求实数a、b、k的值；（21）、过抛物线上点A作直线AC∥x轴，交抛物线于另一点C，求所有满足△EOC∽△AOB的点E的坐标。参考答案1、D、3m-1和m-7是数p的平方根，则\n3m-1=m-7或3m-1+m-7=0m=–3或m=2当m=-3时,3m-1=-10p=100当m=2时,3m-1=5p=252、D、a=20b,b=10ca=200c3、A、设高速列车和普通列车的车速分别为x米8秒、y米/秒，则x+y=600÷3=200（米/秒）所以坐在普通列车上的乘客看见高速列车驶过窗口的时间是：400÷200=2（秒）4、C、连结O1O2,O1A,O1B,O2A,O2BO1O2=O1A=3,O2A=∠O2O1A=90°同理∠O2O1B=90°∴点A、O1、B在同一条直线上，并且∠AO2B=90°AB是圆O1的直径∴S阴影=S⊙1－S弓形AO1B=S⊙1－(S扇形AO2B－S△AO2B)==95、C、方程变形为：，b为实数△=≥0化简得≥0\n(a-4)(a+2)≥0∴a≥4或a≤－26、b＞a＞c共有4+3+3=10名同学制作图片，制作的张数为4,4,4,4,4,5,5,5,6,6,6平均数a==4.9,中位数b=5，众数c=47、75°∠ABC=45°∠DEF=30°∴∠BDE=∠ABC－∠DEF=15°∴∠BDF=∠EDF－∠BDE=90°－15°=75°8、±根据根与系数的关系可得：－1+m=－1+m=－1∴m=1,a=±∴9、C与A重合EF是AC的垂直平分线CG=可证：△CFG≌△AEGFG=EG=可证：△CFG∽△CADFG:AD=CG:CDFG:2=:4FG=∴EF=10、延长AC交⊙O于点F，连结DF∵DE∥BC∴∠DEF=180°－∠ACB=90°∴DF是⊙O的直径∵AB==DE∥BCDE:BC=AD:AB=AE:ACDE:6=AD:=∴DE=4,AD=\n∵AD是切线∴∴AF=∴DF=⊙O的半径R=11、（1）连结PA并延长交x轴于点M，则直线PA的解析式是：y=-x+2点M的坐标是M（2,0）同时MA=PA=说明点A是PM的中点即点M是点P绕点A旋转180°得到点M就是点P1P1(2,0)同样：P2(0,-2)P3(-2,0)(2)重复操作依次是：P4=P8=P,P5=P9=P1,P5=P10=P2,P7=P11=P32010=4×502+2P2010=P2P2010（0，-2）12、设在某一时刻，货车与客车、小轿车的距离均为S千米，小轿车、货车、客车的速度分别为a、b、c（千米/分），并设货车经x分钟追上客车，由题意可得：10(a-b)=S(1)15(a-c)=2S(2)x(b-c)=S有（1）（2）得30（b-c）=S∴S=30t=30－10－5=15(分)13、如图，延长BC交x轴于点F，连结OB，DF，且相交于点N\n有已知得点M（2,3）是OB、AF的中点，即点M为矩形ABFO的中心，所以直线l把矩形ABFO分成面积相等的两部分又因为点N（5,2）是矩形CDEF的中心，所以过点N（5,2）的直线把矩形CDEF分成面积相等的两部分。于是，直线MN即为所求的直线L设直线l的解析式为y=kx+b则2k+b=35k+b=2K=b=因此所求直线l的函数表达式是：14、如图，设CF=m,AF=n易证：RT△AFB∽RT△ABC∴又FC=CD=AB=n即∴或（舍去）又RT△AFE∽RT△CFB即15、解：（1）因为点A（1，4）在双曲线上，所以k=4.故双曲线的函数表达式为.设点B（t，），，AB所在直线的函数表达式为\n，则有解得，.于是，直线AB与y轴的交点坐标为，故，整理得，解得，或t＝（舍去）．所以点B的坐标为（，）．因为点A，B都在抛物线（a0）上，所以解得…………（10分）（2）如图，因为AC∥x轴，所以C（，4），于是CO＝4.又BO=2，所以.设抛物线（a0）与x轴负半轴相交于点D，则点D的坐标为（，0）.因为∠COD＝∠BOD＝，所以∠COB=.（i）将△绕点O顺时针旋转，得到△.这时，点\n(，2)是CO的中点，点的坐标为（4，）.延长到点，使得=，这时点（8，）是符合条件的点.（ii）作△关于x轴的对称图形△，得到点（1，）；延长到点，使得＝，这时点E２（2，）是符合条件的点．所以，点的坐标是（8，），或（2，）.…………（20分）