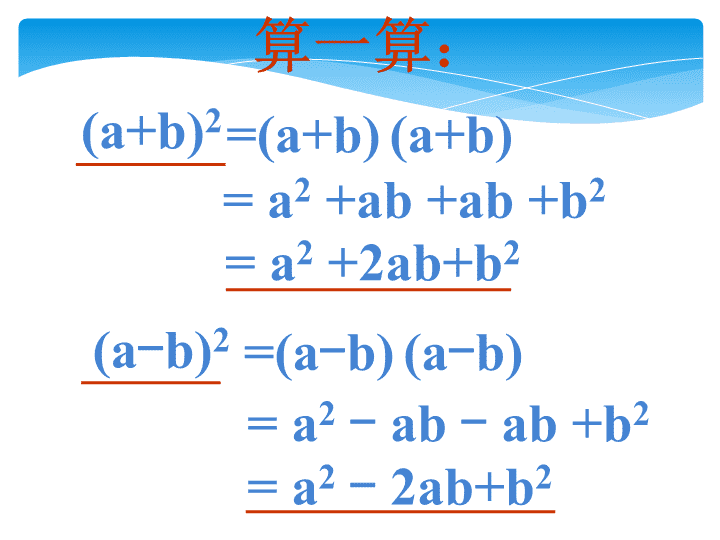初中数学完全平方公式课件 41页

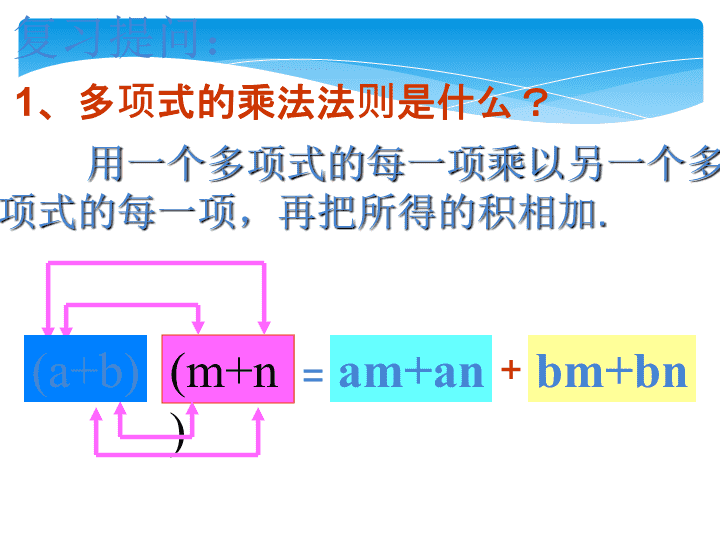
完全平方公式\n复习提问：用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加.1、多项式的乘法法则是什么？am+anbm+bn+=(m+n)(a+b)\n算一算：(a+b)2(a-b)2=a2+2ab+b2=a2-2ab+b2=a2+ab+ab+b2=a2-ab-ab+b2=(a+b)(a+b)=(a-b)(a-b)\nbbaa(a+b)²a²b²abab++完全平方和公式：完全平方公式的图形理解\naabb(a-b)²a²ababb²bb完全平方差公式：完全平方公式的图形理解\n议一议如何计算(a+b+c)2解:(a+b+c)2=[(a+b)+c]2=(a+b)2+2·(a+b)·c+c2=a2+2ab+b2+2ac+2bc+c2=a2+b2+c2+2ab+2ac+2bc\n1992=8.92=利用完全平方公式计算：1012=\n例3计算：(a-b)2=(b-a)2解：原式=\n(-a-b)2=(a+b)2解：原式=\n1.(-x-y)2=2.(-2a2+b)2=你会了吗\n完全平方公式：(a＋b)2=a2＋2ab+b2(a－b)２=a2－2ab+b2(a+b)(a-b)=a2-b2(a＋b)2=a2＋2ab+b2(a－b)２=a2－2ab+b2平方差公式和完全平方公式统称为乘法公式它们有什么区别？\n(3)(a2+b3)2解：原式=(b3a2)2=b6-2a2b3+a4(-a+b)2=(b-a)2(a2+b3)2=(b3-a2)2()2b3=-2×b3×a2+(a2)2（口诀：首项为负换位置）\n(4)(-x2y-)2解：原式=(x2y+)2=x4y2+x2y+(-a-b)2=(a+b)2(x2y)2=+2×x2y×+(口诀：两项为负都变正)\n(a+b)2=a2+2ab+b2(a–b)2=a2–2ab+b2变式训练比一比谁做的快？(1)(-a+3)2；(2)(-m-n)2;要灵活运用哦！\n牛刀小试你能口答吗?(1)(-3a+2b)2；(2)(-4x-y)2;(a+b)2=a2+2ab+b2(a–b)2=a2–2ab+b2\n完全平方公式(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2首平方，尾平方，2倍乘积在中央\n例4.已知a+b=7，ab=12，求a2+b2,a2-ab+b2,(a-b)2的值例6.若x-2y=15，xy=-25，求x2+4y2-1的值终极提高\n例7.已知(a+b)2=4,(a-b)2=6,求(1)a2+b2(2)ab的值例8.已知a-b=2,ab=1,求(a+b)2的值\n例4.运用乘法公式计算(a+1)(a+3)(a+5)(a+7)(3a2+1/2b)(3a2-1/2b)(9a2-1/4b)2练习(a+1)(a+2)(a+3)(a+4)\n拓展与迁移(1)若不论x取何值，多项式x3-2x2-4x-1与(x+1)(x2+mx+n)都相等,求m.n(2)求使(x2+px+8)(x2-3x+q)的积中不含x2与x3项p、q的值(3)求证：x(x+a)=(x+a/2)2-a2/4\n例5.计算例6.已知x2-y2=8，x+y=4，求x与y的值例7.化简(a+1)(a2+1)(a4+1)…(a2000+1)\n能力提高\n例4.已知a+b=7，ab=12，求a2+b2,a2-ab+b2,(a-b)2的值例5.已知，求(1)(2)例6.若x-2y=15，xy=-25，求x2+4y2-1的值\n例2.已知b2=ac，求证：(a+b+c)(a-b+c)(a2-b2+c2)=a4+b4+c4例3已知:若(z-x)2-4(x-y)(y-z)=0求证:X-2y+z=0\n简单应用(a-b)2=(b-a)2(-a-b)2=(a+b)21.(-2x-y)22.(-2a2+b)2=(2x+y)2=(2a2－b)2\n3、公式的逆向使用；4、解题时常用结论：(-a-b)2=(a+b)2(a-b)2=(b-a)2a2+2ab+b2=(a+b)2a2－2ab+b2=(a－b)2\n(2)(a-b)2、(b-a)2、(-b+a)2与(-a+b)2(1)(-a-b)2与(a+b)22、比较下列各式之间的关系：相等相等\nx2+2xy+y2=()2x2+2x+1=()2x+1a2-4ab+4b2=()2a-2bx2-4x+4=()2x-2注意：公式的逆用，公式中各项符号及系数。x+y3、填空：公式的逆向使用；a2+2ab+b2=(a+b)2a2－2ab+b2=(a－b)2\n例题解析学一学例2（巧算）：计算：(1)1022;(2)1972.完全平方公式(a±b)2=a2±2ab+b2的左边的底数是两数的和或差.观察&思考把1022改写成(a+b)2还是(a−b)2?a、b怎样确定？(补充）思考题：计算：1.23452+0.76552+2.469×0.7655\n拓展应用二.完全平方式(注意完全平方式的两种可能情况）2.(跟进训练）多项式x2+mx+4是一个完全平方式,则m=.3.多项式a2-8a+k是一个完全平方式,则k=.4.多项式a2-a+k2是一个完全平方式,则k=.1.(同步P14例2）多项式4x2+M+9y2是一个完全平方式,则M=.\n拓展应用三.公式的逆用1.若a(a−1)−(a2−b)=7，2.计算:(2x−3y)2(2x+3y)23.计算:(ab+1)2−(ab−1)24.x2−y2=6,x+y=−3.求(x−y)2的值.前面讲的完全平方式和某些算式的简便计算方法(如算式1.23452+0.76552+2.469×0.7655)就属于完全平方公式的逆用.下面再举几例加以说明:\n拓展应用四.公式的变形(板书示范)a2+b2=(a+b)2−2aba2+b2=+2ab(a+b)2−(a−b)2=4ab(a−b)2\n拓展应用五.平方法与整体代值1.已知a+b=-5，ab=-6,求a2+b2的值.3.已知x+y=3，xy=-10,求2x2−3xy+2y2的值.4.已知x+y=7，xy=6,求x−y的值.(可考虑两种方法:①将已知条件两边进行平方，再结合整体代值的思想解决；②也可从未知代数式入手，利用公式的变形和整体代值思想解决。）\n拓展应用六.配方法1.(例)已知x2−4x+y2+6y+13=0，求x+y的值。3.已知有理数x，y，z满足x=6−y，z2=xy−9，试说明x=y。2.（跟进训练）已知x2+2x+y2−6y+10=0，求x与y的值。\n拓展应用之挑战极限七.挑战思维极限\n阅读下列过程：(2+1)(22+1)(24+1)=(2-1)(2+1)(22+1)(24+1)=(22-1)(22+1)(24+1)=(24-1)(24+1)=28-1根据上式的计算方法，求:4.阅读与思考拓展应用之挑战极限\n5.248-1能被60和70之间的两个数整除，求这两个数拓展应用之挑战极限\n拓展应用之挑战极限\n7.已知(x3+mx+n)(x2-3x+4)中不含x3和x2项，求m、n的值。拓展应用之挑战极限\n8.a-b=2,b-c=3,求a2+b2+c2-ab-bc-ca的值。拓展应用之挑战极限\n拓展练习真棒！！真棒！！如果把完全平方公式中的字母“a”换成“m+n”，公式中的“b”换成“p”，那么(a+b)2变成怎样的式子?(a+b)2变成(m+n+p)2。怎样计算(m+n+p)2呢?(m+n+p)2=[(m+n)+p]2逐步计算得到：=(m+n)2+2(m+n)p+p2=m2+2mn+n2+2mp+2np+p2=m2+n2+p2+2mn+2mp+2np把所得结果作为推广了的完全平方公式，试用语言叙述这一公式：三个数和的完全平方等于这三个数的平方和，再加上每两数乘积的2倍。仿照上述结果，你能说出(a−b+c)2所得的结果吗?