[初中教育]多边形复习课件 30页

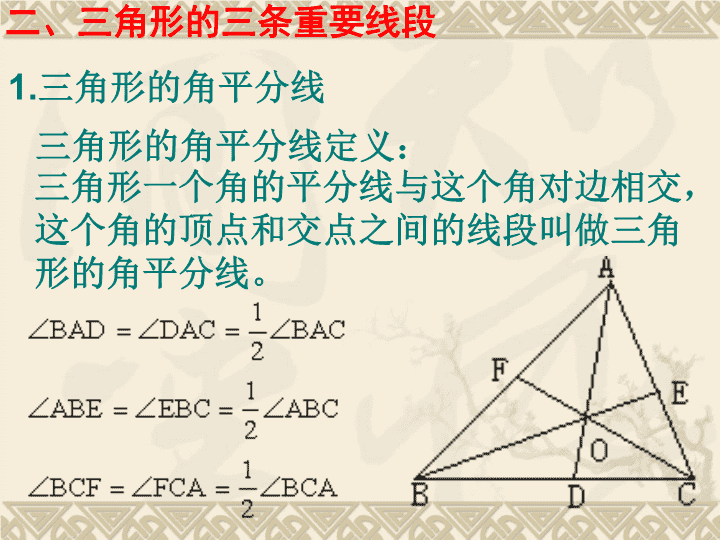
多边形的复习\n由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。一、三角形的概念三角形定义：请回答:(1)怎样表示出右图的三角形?说出它的顶点,内角,外角分别是什么?(2)角和边之间是什么关系?\n三角形一个角的平分线与这个角对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。二、三角形的三条重要线段1.三角形的角平分线三角形的角平分线定义：\n重要图形：在下列三角形ABC中，BO与CO分别是角平分线，∠BOC与∠A有何关系？图（1）图（2）图（3）\n2.三角形的中线三角形的中线定义：二、三角形的三条重要线段在三角形中，连结一个顶点和它的对边中点的线段，叫做三角形的中线。\n如图，AD是三角形ABC的中线，则三角形ABD与三角形ADC的面积关系如何？周长关系呢？应用\n从三角形的一个顶点向它的对边画垂线，顶点和垂足间的线段叫做三角形的高。3.三角形的高三角形的高定义：二、三角形的三条重要线段注意：三角形的角平分线，中线和高都是线段，在画图时不能画成直线，射线。\n三、三角形三条边的关系定理：三角形两边之和大于第三边，三角形两边之差小于第三边。abc\n1.三角形内角和定理：四、三角形的内角和三角形三个内角的和等于180°。方法一：如图，过△ABC中的顶点A作EF//BC。如何理解这个定理?\n方法二：如图，延长△ABC中的BC到D，过C点作CE//AB。\n方法三:如图，在△ABC中BC边上任取一点D，过点D作DE//AB交AC于E，过点D作DF//AC交AB于F。\n（1）直角三角形的两个锐角互余：如图在△ABC中，∠C=90°那么∠A+∠B=90°2.三角形内角和定理推论\n（2）三角形的一个外角等于和它不相邻的两个内角的和。即：如图∠ACD是△ABC的一个外角，那么∠ACD=∠A+∠B。\n如图：AD与BC相交于点O，则∠A+∠C=∠B+∠D。\n如图：∠BDC=∠B+∠A+∠C\n（3）三角形的一个外角大于任何一个和它不相邻的内角。即：如图∠ACD是△ABC的一个外角，那么∠ACD>∠A，∠ACD>∠B。\n注意：三角形的任何一个外角与相邻内角是邻补角，与不相邻的两个内角和相等且大于任何一个不相邻的内角。应用时要搞清楚外角与内角的位置关系，正确运用。ABC\n如图：CD是三角形ABC的外角平分线，说明∠BAC>∠B.\n过n边形一个顶点连对角线，可以得(n－3)条对角线，并且将n边形分成(n－2)个三角形，这(n－2)个三角形的内角和恰好是多边形的内角和，等于(n－2)·180°。五、多边形内角和定理\n六、多边形的外角和定理1、多边形的每个内角与它相邻的外角是邻补角，所以n边形内角和加外角和等于n·180°，外角和等于n·180°－(n－2)·180°=360°1432\n2、多边形外角和定理：任意多边形的外角和等于360°.注意：n边形的外角和恒等于360°，它与边数的多少无关.\n3、多边形最多有三个内角为锐角，最少没有锐角（如矩形）；多边形的外角中最多有三个钝角，最少没有钝角。\n七、用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的密铺，又称做平面图形的镶嵌。这是因为：围绕一点的图形各个内角之和为360度。1.用形状相同的三角形或四边形能铺满地面。2.若用两种正多边形铺满地面，则有以下几种组合：正三与正四、正三与正六、正四与正八…3.若用三种正多边形铺满地面，则有以下几种组合：正三、正四与正六，…\n如图：∠B=∠C，DE⊥BC于E，EF⊥AB于F，∠ADE等于140°，求∠FED的度数50°\nO∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝.540°\n1、一个零件如图所示，按规定∠A等于90°，∠B和∠C应分别等于32和21°，检验工人量得∠BDC等于148°，就断定这个零件不合格，这是为什么？\n3.如图，飞机要从A地飞往B地，因受大风影响，一开始就偏离航线（AB）18°（即∠A＝18°）飞到了C地，经B地的导航站测得∠ABC＝10°.此时飞机必须沿某一方向飞行才能到达能到达B处.那么这一方向与水平方向的夹角∠BCD的度数？2.按图中所给的条件，求出∠1、∠2、∠3的度数.\n4.如图：∠A＝70度，若O为两条角平分线的交点，求∠BOC的度数。5.如图：在△ABC中，∠ABC和∠ACB平分线交于点O，过点O作EF∥BC，交AB于E，交AC于F，且△ABC的周长是24cm，BC＝10cm，求△AEF的周长?\n数学大舞台，敢拼你就来1、一个多边形的每个外角都是，这个多边形的边数是____。2、正十二边形的每个内角的度数是___.3、2n边形与n边形的外角和相差___度.4、一个多边形的每个内角都是，则从一个顶点可以引____条对角线。5、若一个多边形的内角和比外角和多，试求这个多边形的边数。\n巧题妙解:例1:某同学在计算多边形内角和时,漏算了一个内角,得到的结果是2160°,试求这个多边形的边数。点拨：本题中含有两个未知数，一个是多边形的边数，一个是漏掉的内角的度数，却只有一个等式。这种解法的创新之处是挖掘了未知量的隐含条件，即0°＜内角＜180°这是解题的关键。拓展提高：例2一个多边形截去一个角所形成的另一个多边形的内角和是2750°，则原多边形的边数是多少？