整式运算复习初中数学课件 46页

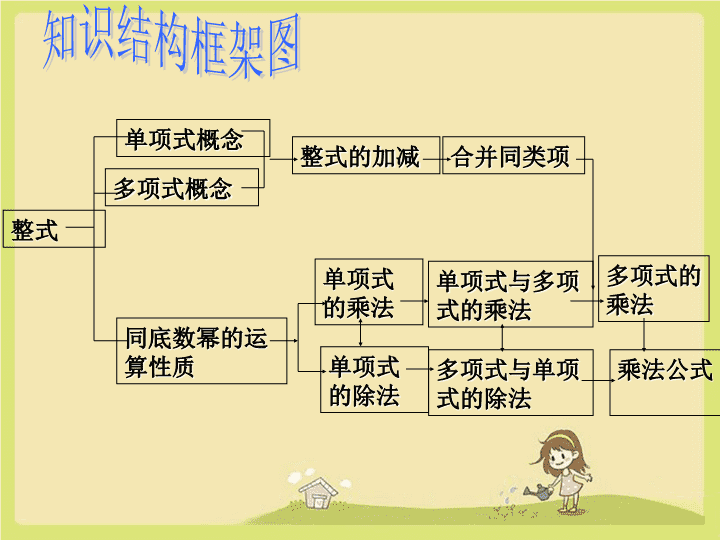
整式的运算\n知识结构框架图整式单项式概念多项式概念整式的加减合并同类项同底数幂的运算性质单项式的乘法单项式的除法单项式与多项式的乘法多项式与单项式的除法多项式的乘法乘法公式\n1、单项式除以单项式2、多项式除以单项式（二）整式的除法1、同底数的幂相乘2、幂的乘方3、积的乘方4、同底数的幂相除5、单项式乘以单项式6、单项式乘以多项式7、多项式乘以多项式8、平方差公式9、完全平方公式（一）整式的乘法\n1、同底数的幂相乘法则：同底数的幂相乘，底数不变，指数相加。数学符号表示：（其中m、n为正整数）（二）整式的乘法练习：判断下列各式是否正确。\n2、幂的乘方法则：幂的乘方，底数不变，指数相乘。数学符号表示：（其中m、n为正整数）练习：判断下列各式是否正确。（其中m、n、P为正整数）\n3、积的乘方法则：积的乘方，先把积中各因式分别乘方，再把所得的幂相乘。（即等于积中各因式乘方的积。）符号表示：练习：计算下列各式。\n4、同底数的幂相除法则：同底数的幂相除，底数不变，指数相减。数学符号表示：（其中m、n为正整数）\n练习：计算判断：\n1.幂的乘方，指数相乘；2.同底数幂的乘法，指数相加；3.同底数幂的除法，指数相减；4.同底数幂的加减法，指数不变(即合并同类项)。温馨提示通法：同底数幂的运算，底数不变，指数运算降一级。运算法则\n5、单项式乘以单项式法则：单项式乘以单项式，把它们的系数、相同字母的幂分别相乘，其余的字母则连同它的指数不变，作为积的一个因式。练习：计算下列各式。\n6、单项式乘以多项式法则：单项式乘以多项式，就是根据分配律用单项式的去乘多项式的每一项，再把所得的积相加。练习：1、计算下列各式。7、多项式乘以多项式法则：多项式乘以多项式，先用一个多项式的每一项去乘另一个多项式的每一项，再把所得的积相加。\n2、计算下图中阴影部分的面积2bba\n8、平方差公式法则：两数的各乘以这两数的差，等于这两数的平方差。数学符号表示：说明：平方差公式是根据多项式乘以多项式得到的，它是两个数的和与同样的两个数的差的积的形式。\n9、完全平方公式法则：两数和（或差）的平方，等于这两数的平方和再加上（或减去）这两数积的2倍。数学符号表示：\n练习：1、判断下列式子是否正确，并说明理由。要特别注意哟，切记，切记！\n2、计算下列式。\n3、简答下列各题：\n（二）整式的除法1、单项式除以单项式法则：单项式除以单项式，把它们的系数、相同字母的幂分别相除后，作为商的一个因式，对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。2、多项式除以单项式法则：多项式除以单项式，就是多项式的每一项去除单项式，再把所得的商相加。\n练习：计算下列各题。\n再见\n思维拓广1.如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式＿＿＿＿＿＿＿＿。ab如图是四张全等的矩形纸片拼成的图形，请利用图中的空白部分面积的不同表示方法，写出一个关于a，b的恒等式_________________.ab\n中考链接abababababababababababa2a2a2a2a2a2b2b2b2b2\n探究拓展☞如图所示，四边形ABCD是正方形，P是对角线BD上一点，过P点作直线MN，EF分别平行于AB，BC，交两组对边于点M，N，E，F。四边形PFDN，PEBM都是正方形，四边形PNAE，PMCF都是矩形，设正方形PEBM的边长为a，正方形PFDN的边长为b。(1)请你动手测量一些线段的长，计算正方形PEBM与正方形PFDN的面积之和以及矩形PNAE与矩形PMCF的面积之和。(2)你能根据（1）的结果判断a2+b2与2ab的大小吗？(3)当P点在什么位置时，有a2+b2=2abABCDEMFNP\n兴趣乐园利用计算机探究（a+b)0，(a+b)1，(a+b)2，(a+b)3，(a+b)4的展开式并观察项及系数的规律后，试着写出(a+b)7的展开式。利用上面的规律，你能解决下面的问题吗？如图，已知蜘蛛从P点沿着L型爬行，去扑捉一只位于Q点的小虫，你能求出蜘蛛有多少种不同的最短爬行路线吗？PQ\n用四个全等的矩形和一个小正方形拼成如图所示的大正方形，已知大正方形的面积是144，小正方形的面积是4，若用x，y表示矩形的长和宽(x＞y)，则下列关系式中不正确的是（　　）yxA.x+y=12B.x－y=2C.xy=35D.x＋y=14422思维拓广\n1、猜想规律。3、已知，求的值。观察下列等式:2、由以上情形，你能求出下面式子的结果吗？_____________.层层递进\n1.19982-1998·3994+19972；2.(2+1)(22+1)(24+1)(28+1)+13.已知x+y=10,xy=24,则x2+y2的值是4.己知x+y=3，x2+y2=5则xy值等于多少？灵活运用\n计算：（3）互帮互助\n计算：巧用公式\n1、运用乘法公式计算:灵活运用\n小诊所判断以下各题是否正确，并说明理由。1.x3+x3=2x3+3=2x6()2.x3.x3=2x3()3.x.x3.x5=x0+3+5=x8()4.x2.(-x)3=-x2+3=-x5()5.x.(-x)m=-x1+m()××××√\n小诊所判断以下各题是否正确，并说明理由。6.(x-y)2.(y-x)3=(x-y)6()7.(-2x3)3=-6x6()8.a3+a4=a7()9.a3a=a3()10.a2.b3(-b)2=-a2.b5()×××××\n快速判断以下各题是否正确。()()()()()()()()()()×√××××××√√基础练习\n1、首项为负时，注意符号的变化。3、乘法运算前面是负号时，乘积的展开式要用括号括起来。2、运用交换律、结合律调整因式或因式中各项的排列顺序，可以使公式的特征更加明显。方法总结\n中考链接例1（山东省聊城市）下列计算错误的是()(A)a·a=a(B)2a÷a=2a(C)(－a)=a(D)(a)=例2（江苏省）用小数表示3×10，结果为()A.-0.03B.-0.003C.0.03D.0.003248232362-1a12-2AC\n中考链接例3（湖北省黄冈市）将（），（-2），（-3）这三个数按从小到大的顺序排列_______________________例4（山东省威海市）若a=1,则a等于（）A.1，0；B.1，3；C.1，-1；D.1，-1，3.16-102a-3D(-2)<（）<(-3)02-116\n思维拓广1.0.125×（-）2.若a=3,a=5,求a2005200681mn2n+m注意：对公式的逆应用可以帮助我们更好的解决问题比较2100与375的大小，请看下面的解题过程解：∵2100=（24）25，375=（33）25，又∵24=16，33=27，而16<27，∴（24）25<（33）25，即2100<375。请根据上面的解题过程，比较355，444，533的大小。3.技巧：当几个数的指数相同时，决定它们大小的是它们的底数。\n计算图中绿色阴影部分的面积.当E在AD上运动时，阴影部分的面积有什么变化？ABCDEab探究拓展☞\n游戏时间在一次数学兴趣活动中，同学们做了一个找朋友的游戏，游戏规定：所持算式相等的两个人是朋友，有五个同学A，B，C，D，E所持纸牌前面分别写有五个算式：2×5，2×5，2×5，（a-1)(d-1),(b-1)(c-1)主持人宣布A，B，C两两是朋友，请大家猜一猜D，E是否是朋友。abcd\n兴趣乐园1776年，美国第一任总统华盛顿宣布美利坚合众国建立。1976年，美国举行了建国200周年的纪念活动。在某中学的黑板报《一日一题》栏目中有一道有趣的题目：1776的最后两位数字是什么？晓明说：“1776年是一个值得纪念的日子，但计算1776可太难了，用计算器也得计算好长时间啊！”小亮看完题后，却不假思索地说：“很简单，是76。”如果不用计算器，你知道小亮使用什么办法很快“算”出来的吗？200200奇怪的自守数\nabm验证公式某住宅小区为更好地保护绿化带，需要修一条小路，abm（1）你能用几种方法计算绿化带的面积？你发现了什么？a(b-m)=ab–am总结：只要路的宽度保持一致，它的形状可以多种多样。abm（2）为了增添小区居民的生活情趣，在绿化带面积不变的情况下请你设计一种修路方案。\n（3）如果像这样再修一条小路，你能计算绿化带的面积吗？abmmabmmabmm(a-m)(b-m)=ab–am-bm+m2\n验证公式你能用面积法验证已经学过乘法公式吗？abbaa-bb平方差公式(a+b)(a-b)=a-b22a还有其他方法来验证平方差公式吗\nabab完全平方公式(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2\n在一次数学兴趣活动中，同学们做了一个找朋友的游戏，游戏规定：所持算式相等的两个人是朋友，有五个同学A，B，C，D，E所持纸牌前面分别写有五个算式：5a×7b，5c×7d，5×7，(a-1)(d-1),(b-1)(c-1)主持人宣布A，B，C两两是朋友，请大家猜一猜D，E是否是朋友。开动脑筋\n比较100与375的大小，请看下面的解题过程2解：∵2100=（24），3375=（3），2525又∵24=16，33=27，而16<27，25∴（24）25<（33），即2100<375。请根据上面的解题过程，比较8131，2741961的大小。技巧：当几个数的指数相同时，决定它们大小的是它们的底数。反之，当几个数的底数相同时，决定它们大小的是它们的指数活学活用