初中全部复习学习资料课件初中数学复习题三 11页

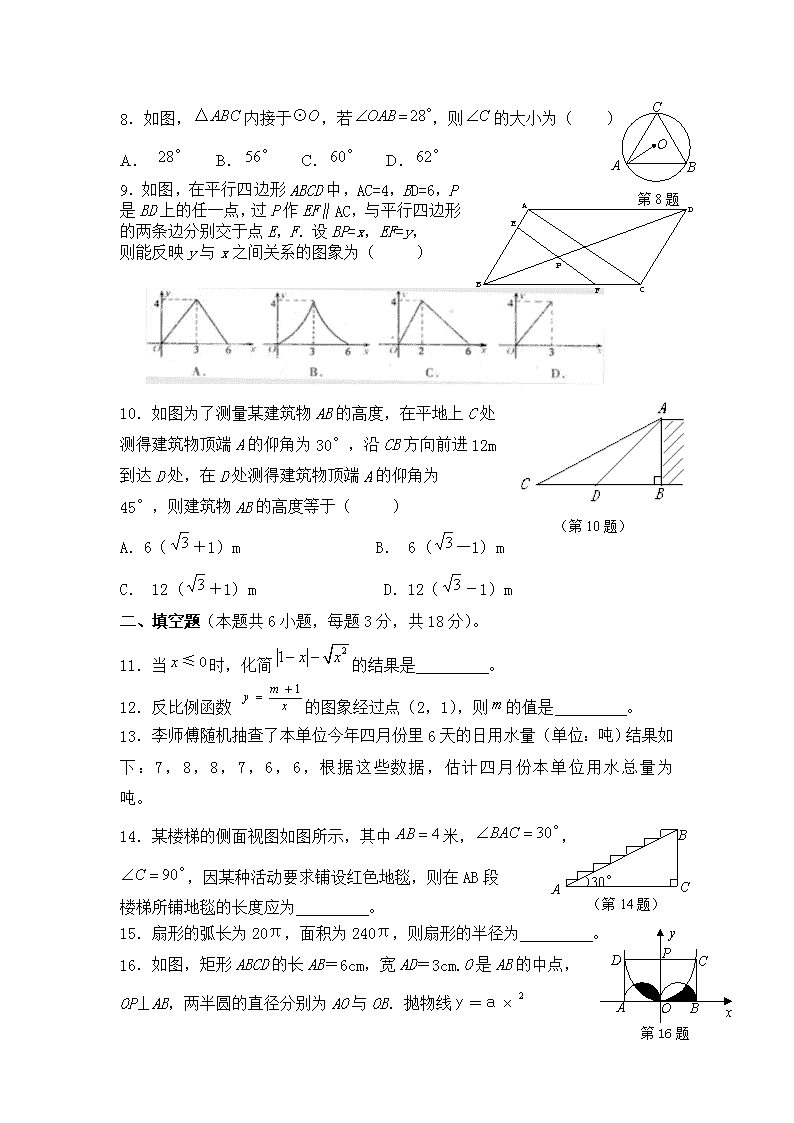
初中数学复习题（三）（限时：120分钟）一、填空题（本题共10小题，每题3分，共30分。每小题有且只有一个选项是正确的）。1．等于（）A．-9B．9C．-27D．272．湛江是个海滨城市，三面环海，海岸线长达1556000米，数据1556000用科学记数法表示为（）A．B．C．　　D．3．下列事件是必然事件的是（）A．阴天一定会下雨B．打开电视机，任选一个频道，屏幕上正在播放篮球比赛节目C．某种彩票的中奖率为1%，买100张彩票一定中奖CDBAEF12D．13名学生中一定有两个人在同一个月过生日4．如图，，于交于，已知，则（）A．20°B．60°C．30°D．45°第4题5．若则，，的大小关系是（）A．　　B．　　C．D．6．向上发射一枚炮弹，经x秒后的高度为y公尺，且时间与高度关系为y=ax2+bx。若此炮弹在第6秒与第14秒时的高度相等，则在下列哪一个时间的高度是最高的（）A.第8秒B.第10秒C.第12秒D.第15秒。7．如右图，矩形的两条对角线相交于点，ODCAB第7题，则矩形的对角线的长是（）A．2B．4C．D．\n8．如图，内接于，若，则的大小为（第8题CABO）A．　　B．　　C．　　D．9．如图，在平行四边形ABCD中，AC=4，BD=6，P是BD上的任一点，过P作EF∥AC，与平行四边形的两条边分别交于点E，F．设BP=x，EF=y，则能反映y与x之间关系的图象为（　）（第10题）　　10．如图为了测量某建筑物AB的高度，在平地上C处测得建筑物顶端A的仰角为30°，沿CB方向前进12m到达D处，在D处测得建筑物顶端A的仰角为45°，则建筑物AB的高度等于（）A．6（＋1）mB．6(—1)mC．12(＋1)mD．12（－1）m二、填空题（本题共6小题，每题3分，共18分）。11．当时，化简的结果是。12．反比例函数的图象经过点（2，1），则的值是。13．李师傅随机抽查了本单位今年四月份里6天的日用水量（单位：吨）结果如下：7，8，8，7，6，6，根据这些数据，估计四月份本单位用水总量为吨。14．某楼梯的侧面视图如图所示，其中米，（第14题）BCA30°，，因某种活动要求铺设红色地毯，则在AB段ACBDPOxy第16题楼梯所铺地毯的长度应为。15．扇形的弧长为20π，面积为240π，则扇形的半径为。16．如图，矩形ABCD的长AB＝6cm，宽AD＝3cm.O是AB的中点，OP⊥AB，两半圆的直径分别为AO与OB．抛物线ｙ＝ａｘ\n经过C、D两点，则a＝，图中阴影部分的面积是cm2。三、解答题（本大题共9小题，共102分，解答时应写出文字说明、证明过程或者是演算步骤）。17．（8分）解不等式组，并把解集在数轴上表示出来．EBCGDFA18．（10分）如图，已知正方形，点是上的一点，连结，以为一边，在的上方作正方形，连结．求证：。19．（10分）如右图，是由四个直角边分别是3和4的全等的直角三角形拼成的“赵爽弦图”，小亮随机的往大正方形区域内投针一次，求：（1）针扎在任意一个三角形上的概率；（2）针扎在阴影部分的概率。20．（10分）给出三个多项式：请你选择其中两个进行加法运算，并把结果因式分解。BCA21．（12分）如图，正方形网格中，△ABC为格点三角形（顶点都是格点），将△ABC绕点A按逆时针方向旋转90°得到．（1）在正方形网格中，作出；（不要求写作法）（2）设网格小正方形的边长为1cm\n，用阴影表示出旋转过程中线段BC所扫过的图形，然后求出它的面积．（结果保留）22．（12分）已知：如图，在△ABC中，∠ABC＝90°，以AB上的点O为圆心，OB的长为半径的圆与AB交于点E，与AC切于点D．（1）求证：BC＝CD；（2）求证：∠ADE＝∠ABD；（3）设AD＝2，AE＝1，求⊙O直径EB的长．23．（12分）有一种螃蟹，从海上捕获后不放养，最多只能存活两天．如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去．假设放养期内蟹的个体质量基本保持不变，现有一经销商，按市场价收购这种活蟹1000kg放养在塘内，此时市场价为每千克30元，据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需支出各种费用为400元，且平均每天还有10kg蟹死去，假定死蟹均于当天全部销售出，售价都是每千克20元．(1)设x天后每千克活蟹的市场价为p元，写出p关于x的函数关系式；(2)如果放养x天后将活蟹一次性出售，并记1000kg蟹的销售总额为Q元，写出Q关于x的函数关系式．(3)该经销商将这批蟹放养多少天后出售，可获最大利润(利润=Q－收购总额)？24．（14分）如图，已知抛物线L1:y=x2-4的图像与x有交于A、C两点，（1）若抛物线l2与l1关于x轴对称，求l2的解析式；（2）若点B是抛物线l1上的一动点（B不与A、C重合），以AC为对角线，A、B、C三点为顶点的平行四边形的第四个顶点定为D，求证：点D在l2上；（3）探索：当点B分别位于l1\n在x轴上、下两部分的图像上时，平行四边形ABCD的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，并求出它的面积；若不存在，请说明理由.25．（14分）两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED按图1所示的位置放置，A与C重合，O与C重合．（1）求图1中，A，B，D三点的坐标；（2）Rt△AOB固定不动，Rt△CED沿x轴以每秒2个单位长的速度向右运动，当D点运动到与B点重合时停止，设运动x秒后Rt△CED和Rt△AOB重叠部分面积为y，求y与x之间的函数关系式；（3）当Rt△CED以（2）中的速度和方向运动，运动时间x=4秒时Rt△CED运动到如图2所示的位置，求经过A，G，C三点的抛物线的解析式；（4）现有一半径为2，圆心P在（3）中的抛物线上运动的动圆，试问⊙P在运动过程中是否存在⊙P与x轴或y轴相切的情况，若存在，请求出P的坐标，若不存在，请说明理由．\n初中数学复习题（三）（答卷）本试卷限时120分钟完成一、选择题（3*10=30分）题号12345678910答案二、填空题（3*6=18分）11、12、13、14、15、16、，17、（本题满分8分）18、（本题满分10分）三、解答题（9题共102分）\n19、（本题满分10分）20、（本题满分10分）\n21、（本题满分12分）22、（本题满分12分）\n23、（本题满分12分）\n24、（本题满分14分）\n25．（本题满分14分）