初中数学课件中考操作题讲解ppt课件 20页

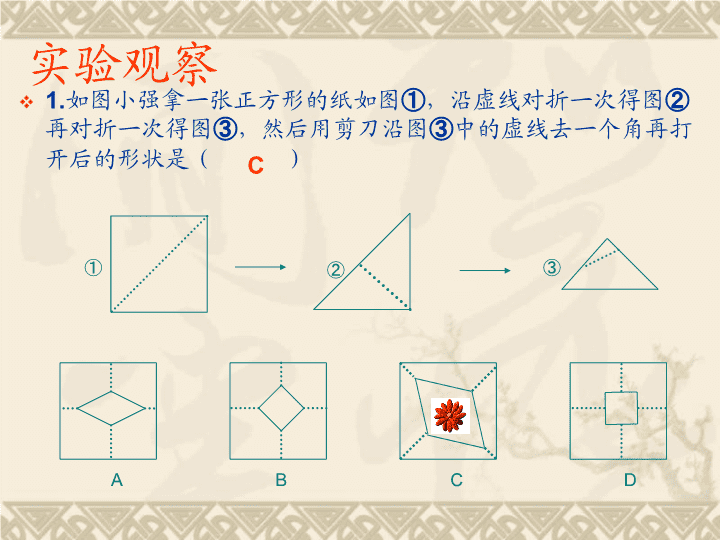
动手操作题中考数学专题复习天马行空官方博客：http://t.qq.com/tmxk_docin；QQ:1318241189；QQ群：175569632\n操作性问题1.画图问题；2.3.4.5.网格网问题；\n1.如图小强拿一张正方形的纸如图①，沿虚线对折一次得图②再对折一次得图③，然后用剪刀沿图③中的虚线去一个角再打开后的形状是（　　　）实验观察③②①ABCDC\n2.将一张矩形对折再对折如图所示，然后沿图中虚线剪下得到①、②两部分，将①展示后得到的平面图形是（　　　）A、矩形B、三角形C、梯形D、菱形①②DD、菱形\n3.将一长方形纸片按如图方式折叠，BC、BD为折痕，折叠后AB,BE在一条线上.则∠CBD的度数为（　　　　）A、60°B、75°C、90°D、95°C、90°CAE\n1.（2005河北省）将一正方形纸片按图5中（1）、（2）的方式依次对折后，再沿（3）中的虚线裁剪，最后将（4）中的纸片打开铺平，所得图案应该是下面图案中的（）B小试牛刀:\n2.（2005常州）若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面的正方体棱长为1，如果塔形露在外面的面积超过7，则正方体的个数至少是【】A、2B、3C、4D、5【求解策略】在观察分析的基础上，对问题的本质要有深刻的认识，以此确定求解方案．本问题中，表面上看本题的设问强调的是让学生“求出正方体的个数”，但仔细分析一下其实解题的关键在于学生能否“用正方体的个数（n）来表示塔形露在外面的面积（S）”，\n2.（常州）若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面的正方体棱长为1，如果塔形露在外面的面积超过7，则正方体的个数至少是【】A、2B、3C、4D、5图1图2图3C\n3.（宁波市）已知:如图，平行四边形ABCD．1.画出平行四边形A1B1C1D1，使平行四边形A1B1C1D1与平行四边形ABCD关于直线MN对称．2.画出平行四边形A2B2C2D2，使平行四边形A2B2C2D2与平行四边形ABCD关于点O中心对称.3.平行四边形A1B1C1D1与平行四边形A2B2C2D2是对称图形吗？若是，请在图上画出对称轴或对称中心．A1B1C1D1A2B2C2D2PQ\n4.如图，平面直角坐标系中，△ABC为等边三角形，其中点A、B、C的坐标分别为（－3，－1）、（－3，－3）、（－3＋，－2）．现以y轴为对称轴作△ABC的对称图形，得△A1B1C1，再以x轴为对称轴作△A1B1C1的对称图形，得△A2B2C2．⑴求点C1、C2的坐标；（2）能否通过一次旋转将△ABC旋转到△A2B2C2的位置？你若认为能，请作出肯定的回答，并直接写出所旋转的度数；你若认为不能，请作出否定的回答（不必说明理由）；\n设计思考1.如图所示两个正方形的花坛，准备把每个花坛都分成形状相同的四块，种不同的花草，下面左边两个图案是设计示例，请你再设计两个不同的图案。\n2.某地板厂要制作一批正六边形的地板砖，为适应市场多样化的需要，要求在地板砖上设计图案能够把正六边形6等分，请你帮助他们设计等分方案（至少设计两种）。\n3.现有一块形如母子正方形的板材ABCDEF，木工师傅想先把它分割成几块，然后适当拼接成某种特殊形状的板面（要求板材不能有剩余，拼接时不重叠无空隙），请按下面要求帮助木工师傅分别设计一种方案。（1）板面形状为等腰梯形。（2）板面形状为正方形。请在方格中的图形中画出分割线，在相应的下边方格纸中画出拼接后的图形。ABCDEF等腰梯形正方形\n应用举例1.已知在△ABC中AB＝AC,AD⊥BC于D，且AD＝BC＝4，若将此三角形沿AD剪开成两个三角形，在平面上把这两个三角形再拼成一个四边形，你能拼出所有的不同形状的四边形吗？画出你所拼的四边形的示意图（标出图中直角），并分别写出所拼四边形对角线的长（只写结果）。ABCD\n两条对角线分别是4和4两条对角线分别是2和2两条对角线分别是2和两条对角线都是242424242\n2.取一张矩形的纸进行折叠，具体操作如下：第一步：先把矩形ABCD对折，折痕为MN（图①）。第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上对应点为B’（图②）。第三步：沿EB′线折得折痕EF（图③）利用展开图④：（1）△AEF是什么三角形？（2）证明你的结论。ABCDMN图①ABCDMNEB′图②ACDMNEB′BFA图③ACDMNEB′BPF图④\n操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处。将三角板绕P点旋转，三角板的两直角边分别交射线AC，CB于D、E两点。图1、2、3是旋转三角板得到的图形中的3种。探究：（1）三角板绕P点旋转，观察线段PD和PE之间有什么大小关系？它们的大小关系是，并以图(2)为例，加以证明。操作探究图(1)图(2)\n（2）三角板绕P点旋转。当△PBE是等腰三角形时,求CE的长.（3）若将三角板直角顶点放在斜边AB上的M处，且AM：MB＝1：3，和前面一样操作，试问线段MD和ME之间又有什么关系？请直接写出结论，不必证明（图4供操作用）。结论为。图(3)图(4)\n再见\n有一长方形的餐厅长10m，宽7m，现摆放两套同样大小的圆桌和椅子占据的地面部分可看成半径为1.5m的圆形（如图），在保证通道最狭窄外的宽度不小于0.5m的前提下，问此餐厅内能否摆下三套或四套同样大小的圆桌和椅子呢？请选择摆放三套或四套同样大小的圆桌中一种在方格纸中画出设计示意图。（要求画出的图符合比例要求）思考题