高中数学高中一年级(上册)复习资料全 13页

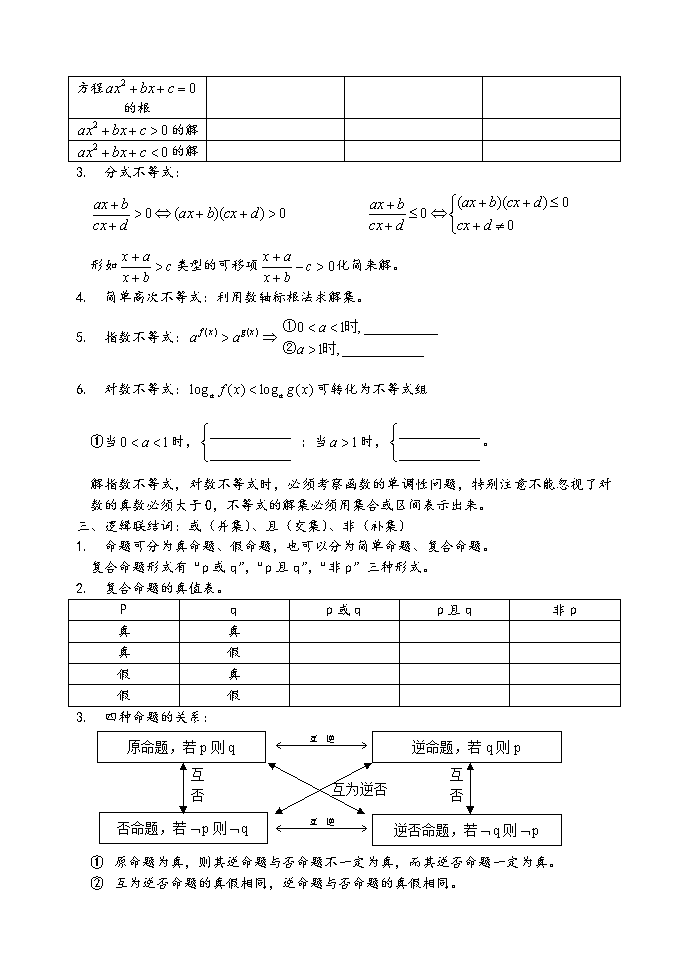
第一章集合与简易逻辑一、集合：1.集合的定义：集合的表示方法：数集：(复数集)集合的特性：2.元素与集合的关系：集合与集合的关系：空集是任何集合的__________，是任何非空集合的_______________。任何一个集合都是他自身的____________。集合{}的子集个数有____个，真子集有____个，非空真子集有____个。当时，一般要分与两种情况。3.交集是指A与B中公共元素构成的集合，A∩B={x|}并集是指所有属于集合A或属于集合B的元素构成的集合，A∪B={x|}一般采用画出数轴来求两个集合的交集或并集。有关系式：①若A∩B=A，则____________；②若A∪B=A，则_____________；③__________、____________。二、不等式解法：1.绝对值不等式解法：a>0a=0a<0|x|a的解集①②③2.二次不等式：与二次函数以为例的图象\n方程的根的解的解3.分式不等式：形如类型的可移项化简来解。4.简单高次不等式：利用数轴标根法求解集。5.指数不等式：6.对数不等式：可转化为不等式组①当时，；当时，。解指数不等式，对数不等式时，必须考察函数的单调性问题，特别注意不能忽视了对数的真数必须大于0，不等式的解集必须用集合或区间表示出来。三、逻辑联结词：或（并集）、且（交集）、非（补集）1.命题可分为真命题、假命题，也可以分为简单命题、复合命题。复合命题形式有“p或q”，“p且q”，“非p”三种形式。2.复合命题的真值表。Pqp或qp且q非p真真真假假真假假3.四种命题的关系：互为逆否互否互否原命题，若p则q逆命题，若q则p逆否命题，若q则p否命题，若p则q①原命题为真，则其逆命题与否命题不一定为真，而其逆否命题一定为真。②互为逆否命题的真假相同，逆命题与否命题的真假相同。\n4.充要条件：①若但BA，则A是B的___________条件。②若AB但，则A是B的___________条件。③若，则A是B的___________条件。④若AB且BA，则A是B的___________条件。四、恒成立问题：1.恒成立，可令，函数图象恒在轴上方。等价于：2.恒成立，等价于：例：已知不等式恒成立（或解集为R），求的取值范围。第二章函数一、函数及有关性质。1.函数定义：中，自变量的取值范围为函数的定义域。当时，叫函数值。所有函数值的集合叫做函数的值域。2.映射的定义：两个允许：两个不允许：3.同一函数：①_______相同。②_________相同。③值域相同。（可由①②得③）4.函数定义域求法：使函数有意义的条件。①整式函数（一次函数、二次函数）定义域为R。②分式函数的分母不为0。③偶次根式函数，被开放数大于或等于0。（的）④对数函数的底数大于0且不等于1，真数大于0。\n有多个限制条件的转化为不等式组求定义域。5.函数的单调性：①定义：②逆运用：当在区间[m，n]上为增函数时，若则有：当在区间[m，n]上为减函数时，若则有：③常用函数的单调性：Ⅰ.一次函数，当时为增函数；当时为减函数。Ⅱ.二次函数，当时在为减函数；在为增函数。当时在为增函数；在为减函数。与开口方向和对称轴有关。Ⅲ.反比例函数在上均为减函数；在上均为增函数。Ⅳ.，当时为减函数；当时为增函数。Ⅴ.，时，在上为减函数；当时，在上为增函数。6.反函数：求函数的反函数的方法：（1）先根据原函数的定义域求出其值域（2）由解出（3）将中的互换，即得反函数标明定义域有关性质：（1）原函数与反函数的定义域和值域正好互换，原函数过点，则反函数过点。（2）互为反函数的图象关于成轴对称图形。\n（3）原函数与反函数的单调性相同。7.函数得奇偶性：存在奇偶性得条件时定义域必须关于原点对称，在定义域内，将后（1）若，则为偶函数。（2）若，则为奇函数。有关性质：（1）偶函数得图象关于轴对称，在对称区间上的单调性相反。（2）奇函数得图象关于原点对称，在对称区间上的单调性相同。8.求函数值域的基本方法（1）利用函数的单调性求值域：若在上为增函数则其值域为若在上为减函数则其值域为。（2）配方法：二次函数当，有最小值，值域为；当时，有最大值，。（3）反表示法：即利用反函数的定义域既为原函数的值域。例如：求的值域。（4）换原法：还原注意新元素的范围。例如：求的值域。（5）判别式法：形如：类型，可转化为关于的一元二次方程有解，求值域。（6）图象法。9.周期性：若函数对于最小正周期，使，则称为函数的最小正周期。\n10.对称性：若则称为的对称轴二、指数函数与对数函数（一）指数1根式与分数指数幂：=运算法则：2指数函数的图象和性质：单调性定点值域定义域性质图象减函数增函数3指数方程：（1）（化成底数相等）（2）可换元后求解，令4指数复合函数的单调性：（1）时，的单调性相反（2）时，的单调性相同（一致）（二）对数函数1对数式与指数式互化：；2对数的运算法则：\n对数恒等式：换底公式：3对数函数的图象和性质性质单调性定点值域定义域图象减函数增函数（1）当与都大于1或都小于1时，（2）当与一个大于1另一个小于1时，4对数方程：5对数函数复合形式的单调性：的定义域内（1）时，的单调性相反，\n（2）时，的单调性相同。三二次函数，判别式1与轴的交点个数：（1），有个交点（2），有个交点，（3），无交点。当时，方程有两个实根：。则由韦达定理（根与系数的关系）知：，2一元二次方程实根问题（以为例）oxyxo（1）有两正根（2）有两个负根（3）有一正一负的根3()区间根问题仅一个根在内\nm图象nnmnmmm充要条件4二次函数()在区间内的最值问题:(1)当时,函数在上为增函数。,;(2)当时。,;(3)当时。,;(4)当时,函数在上为减函数。，。例:已知在上的最小值为13,求a的值.解:综上所述:满足条件的或。\n四图象变换，设1.平移：2.3.对称：4.五复合函数：1若函数，则称为关于的复合函数。（1）为内函数，为外函数。（2）的值域，既为的定义域。2已知的表达式，求的表达式，可采用换元或凑项的方法。例：已知函数，求(法一)：令，则，（法二）：，整体替换，将3已知的定义域，求的定义域例已知，求的定义域解：，令将。4复合函数的单调性规律增增减减\n增减增减增减减增第三章数列一、数列的基本知识：1.数列的定义：2.数列的基本表示方法：3.通项公式：，用含有n的代数式表示。4.数列的前n项和，，已知数列的前n项和，求的方法：①n=1时，；②时，验证，是否适合，若适合，则；若不适合，则也可以判断是否等于0，若则；若，二、等差数列1.定义：即：，首项为，公差d。2.通项公式：==（关于n的一次函数）前n项和公式：==（关于n的二次函数，不含常数项）可化为。3.等差数列的性质：①②若m+n=p+q，则：若m+n=2k，则：\n③仍成等差数列④若，则数列为_______________数列。前n项和有_______值。满足:，找分界项。（也可以用二次函数特点求）若，则数列为_______________数列。前n项和有_______值。满足:，找分界项。（也可以用二次函数特点求）例：已知等差数列的首项为31，公差为-4，求的最大值。⑤若等差数列共有2n+1项，则，，。三、等比数列。1.定义：即：，首项，公比为q（q≠0）。2.通项公式：=前n项和公式：=；当q=1时，。3.等差数列的性质：①②若m+n=p+q，则：若m+n=2k，则：③仍成等比数列四、数列求和方法：1.特殊数列求和：①等差数列求和；②等比数列求和；③常数数列求和；2.分组求和法：一般可转化为等差数列，等比数列求和。通项结构例：求的和。3.裂项求和法：\n例：求的和。4.错位相减法：（q倍求和法）通项结构例：求的和。