高中数学毕业会考圆锥曲线复习资料 9页

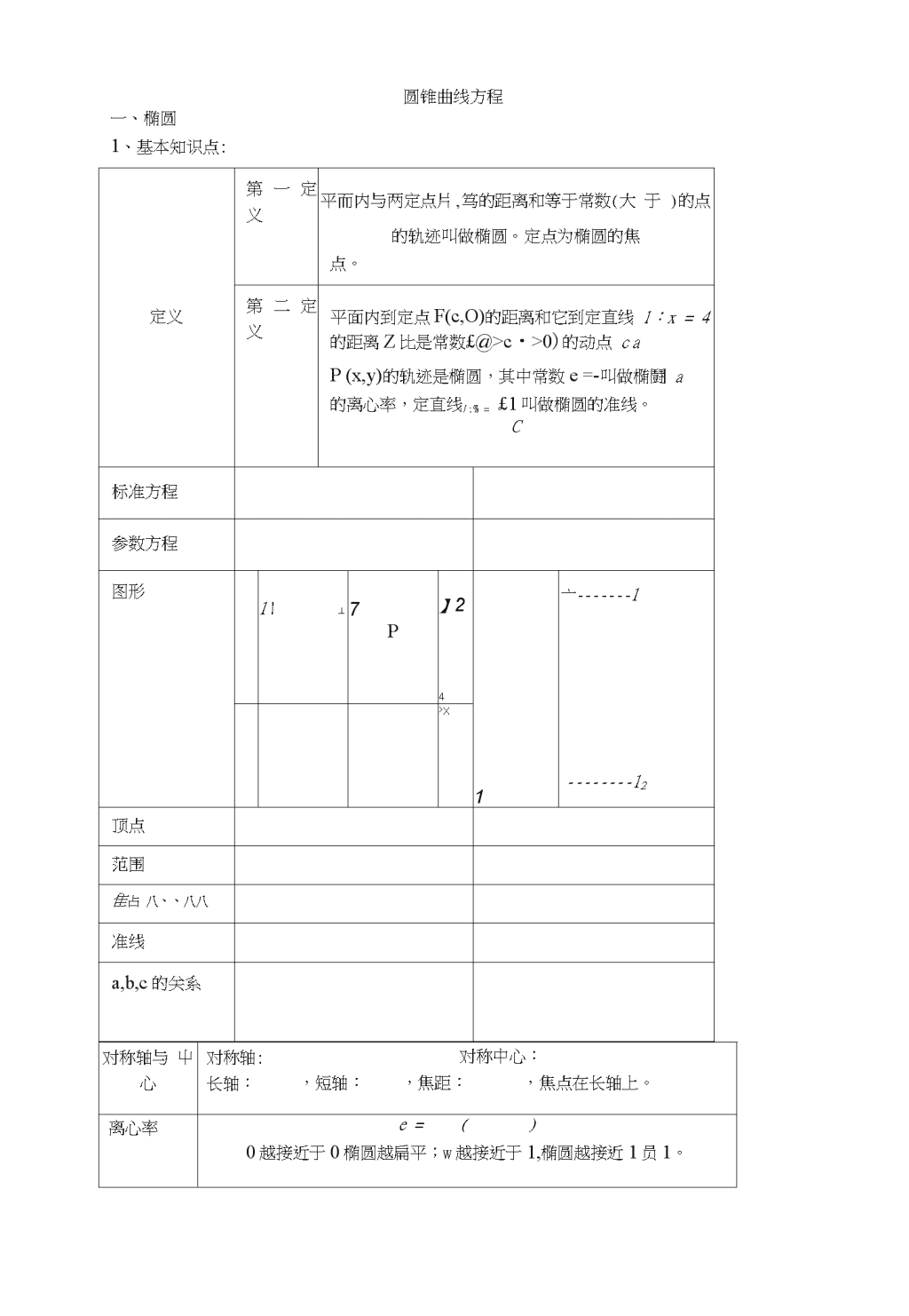
圆锥曲线方程一、椭圆1、基本知识点:定义第一定义平而内与两定点片,笃的距离和等于常数(大于)的点的轨迹叫做椭圆。定点为椭圆的焦点。第二定义平面内到定点F(c,O)的距离和它到定直线l：x=4的距离Z比是常数£@>c・>0)的动点caP(x,y)的轨迹是椭圆，其中常数e=-叫做椭鬪a的离心率，定直线/:%=£1叫做椭圆的准线。C标准方程参数方程图形1\丄7P】241亠112>X顶点范围隹占八、、八八准线a,b,c的关系对称轴与屮心对称轴:长轴：对称中心：，短轴：，焦距：，焦点在长轴上。离心率e=()0越接近于0椭圆越扁平；w越接近于1,椭圆越接近1员1。\n焦准距焦点到对应准线的距离教焦准距，用P表示，p=通经过焦点而垂直于焦点所在对称轴的弦长叫通径，其值为2ep=焦点三角形称APFjFo叫椭圆的焦点三角形，面积公式：S空中广椭圆系方程1具有公共焦点的椭圆系方程：二+丄丁=1(其中k>c2)kk-c222具有和同离心率的椭圆系方程：亠+\=2(。>b>0,/1>0)a中点弦以点M(x,y)为中点的弦的斜率为则£=以点M(x,y)为中点的弦的斜率为k,则£=焦半径PF严|昭卜PF匸|^|=2、椭圆上是否存在点P与两焦点片,尸2连接使ZF,PF2=90°(以片,笃为直径的圆是否与椭圆存在交点)Bbpy®b>cH寸0<£<0个②/?=—7+>1A\nX2y24、直线y=kx+m与椭圆笃+—=1的位置关系：cTb_建立直线与椭圆的方程组，化成关于兀或)；的-•元二次方程\nkx+mx2+2kmm2*门(二次项系数人于0)A>0<=>H线与椭圆相交；有2个焦点。△=0o直线与椭I员I相切；冇1个焦点。A<0<=>直线与椭圆相离；没有焦点。二、双曲线：1基本知识点：第一定义：平面内与两定点片，竹的距离差的绝对值等于常数(小T)的点的轨迹叫做双曲线。两定点为双曲线的焦点。平血内到定点F(c,0)的距离和它到定玄线/：x=—的距离之C比是常数£(c>d>0)的动点P(x,y)的轨迹是双曲线，其定义a第二定义:中常数阳一叫做双曲线的离心率，定直线/:x=£l叫做双IlliClc线的准线。标准方程图形顶点范围焦点准线\na,b,c的关系eo对称轴对称轴：，对称中心：\n与中心实轴：，虚轴：，焦距：，焦点在实轴上。离心率()幺越小双Illi线开口越小，幺越大双曲线开口越大焦准距焦点到对应准线的距离教焦准距，用p农示，p二通径过焦点而垂直于焦点所在对称轴的弦长叫通径，其值为2ep=隹占二八、、八—*角形称\PF,F2叫椭圆的焦点三角形，而积公式：S旳已二双曲线系方程r2具有公共焦点的椭圆系方程：〉乍=1(其中()kk_L具有相同相同渐近线系方程为：中点弦以点M(兀,y)为中点的弦的斜率为则2=以点M(x,y)为中点的弦的斜率为k,则k=焦半径PF严\PF2\=1^1=1^1=2、等轴双曲线:方程:渐近线:3、直线y=kx+m与双曲线二—匚二1的位置关系:cT建立直线与双曲线的方程组，化成关于兀或y的一元二次方程y=kx+m宀°]k2}wb~)22kmnT.门厂x——-1=0b2b1①当二项式系数为0,既飞ak2=o=>z：=±—时,a直线平行于渐近线与双曲线相交,有一个交点。②当k^±-时：方程为一元二次方程a△〉()O直线与双曲线相交；冇2个焦点。△=0o直线与双曲线相切；有1个焦点。△vOo直线与双曲线和离；没有焦点。三、抛物线：1、基本知识；定义平面内与一定点F和一条定直线/的距离相等的点的轨迹叫抛物线，点F叫\n做抛物线的焦点，立线/叫做抛物线的准线。标准方程y2=2*=X2=X2=图形通式顶点对称轴焦点离心率准线通径过焦点而垂玄于焦点所在对称轴的弦长叫通径，其值为2即?=焦半径2、y=怂+m与抛物线y2=2px的位置关系:建立直线与抛物线的方程组，化成关于x或y的一元二次方程y=kx-\-my2=2px=^>k2x2+（2km-2p）x+m2=0①当二项式系数为0,既k2=0^k=0时，肓线平行于对称轴与抛物线相交，有一个交②当Ph（）时：方程为一元二次方程△〉（）o直线与抛物线相交；冇2个焦点。A=0o直线与抛物线相切；有1个焦点。△vOo直线与抛物线相离；没有焦点。3、定值顶点问题：（1）直线I过抛物线）"=2px焦点且与抛物线交于/1（坷,y2）,B（x2,y2）两点:①以AB为肓径的圆与抛物线准线相切。②过点A,B做准线/的垂线，垂足为C,DoTTZCFD=-,AD与BC相较于原点。2③XyX2=,OAOB=（2）直线/与抛物线y2=2px相交于A（州，儿）,凤兀2，儿）两点，若OAOB=0,贝ij;\nX"=4/异，y}y2=-4/?2,s线恒过点（2p,0））0椭圆及其标准方程习题1.求适合下列条件的标准方程(1)两个焦点坐标分别是(-3,0),(3,0),椭圆经过点(5,0)(2)两个焦点坐标分别是(0,5),(0,-5),椭圆上一点P到两焦点的距离和为26o222.椭圆—+=1的焦点坐标是25169223.椭圆乞+丄=1一上一点P到站个焦点的距离的和为1312224.已知椭圆的方程为—+丄〒=1,焦点在x轴上，则m的取值范围是16nr225.椭圆二+丄=1上一点P到一个焦点的距离为5,则P到另一个焦点的距离为2596.椭圆2x2+3/=12的两焦点之间的距离是7.若三角形ABC的两个顶点坐标A(-4,0),3(4,0),三角形ABC的周长为18,则顶点C的轨迹方程为椭圆的几何性质习题1.2.3.4.求椭圆25x2+y2=25的氏轴和短轴的长、焦点和顶点坐标、准线和离心率。椭圆的一个顶点与两个焦点构成等边三角形，则此椭圆的离心率是r2v2Y2V2已知椭圆C：二+二=1L椭圆—4-^=1有相同离心率，贝IJ椭圆C的方程可能是CTb~22—+—=m2(mH0)8422若椭圆一~=1(。>b>0)的两准线间的跖.离为—-—,离心4'-为a~b~34822—1664x2y2C一+丄=1D以上都不可能82.16>/3T'则椭圆的标准方程为5.已知点A(l,2)在椭圆話+誇=1内,F的坐标为(2,0),在椭圆上求一点P使|PA|+2|PF|最双曲线及其标准方程习题1.双曲线9x2-16y2=1的焦距是2.已知定点片(-2,0)、鬥(2,0),在满足下列条件的平面内动点P的轨迹中为双曲线的是A|P用-『厲|=±3B\PF]-\PF2\=±4C\PF}\-\PF2\=±5D『尸『一『尸2『=±4\n1.已知双曲线土-丄=1上的一点P到双曲线的一个焦点的距离为3,则点P到另一个焦点的距离916为2.若动点P到片（-5,0）与点P到F2（5,0）的距离的差为±8,则P点的轨迹方程是—3.P是双曲线x2-y2=l6的左支上一点，片迅分别是左、右焦点，则『用一|“2卜双曲线的几何性质习题1.双1111线的实轴长与虚轴长之和等于其焦距的血倍，且一个顶点坐标为（0,2）,则双曲线的标准方程为o222.双曲线与椭圆—+二=1有相同的焦点，它的一条渐近线为）=-兀，则双曲线方程为166433.已知双曲线的渐近线方程为y=±-x,则双曲线的离心率为4.准线方程为）‘，=±1,离心率为血的双曲线的方程是225.已知双曲线—-^=1,F为其右焦点，A（4,l）为平而上一点，点P为双曲线上一点，求457\pa\^-\pf\的最小值。抛物线及其标准方程习题1.分别满足下列条件的抛物线的标准方程。（1）过点（3.-4）；（2）焦点在直线兀+3y+15=0上已知抛物线的焦点为（3,3）,准线为x轴，求抛物线的方程。2.点M与F（0,-2）的距离比它到直线Z:y-3=0的距离小1,求点M的轨迹方程。3.已知点（-2,3）与抛物线/=2/7x（/?>0）的焦点的距离是5,求p的值。4.抛物线y=的准线方程是y=2,贝巾为5.圆心在抛物线=2x上，且与x轴和该抛物线的准线都相切的一个圆的方程是