最新初中数学：半角模型精品课件 21页

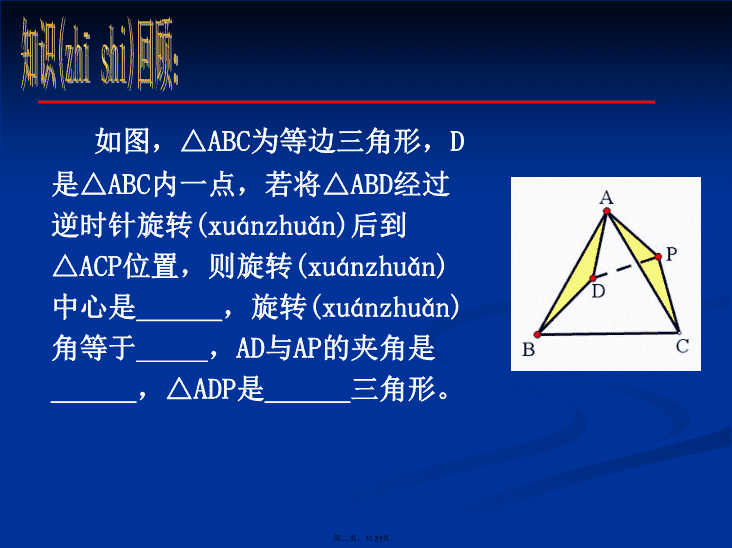
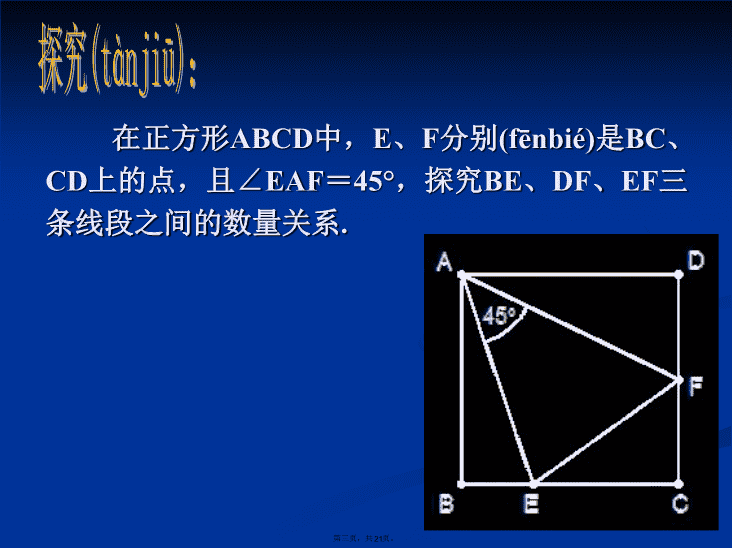
旋转(xuánzhuǎn)的应用第一页，共21页。\n如图，△ABC为等边三角形，D是△ABC内一点，若将△ABD经过逆时针旋转(xuánzhuǎn)后到△ACP位置，则旋转(xuánzhuǎn)中心是______，旋转(xuánzhuǎn)角等于_____，AD与AP的夹角是______，△ADP是______三角形。点A60°等边知识(zhīshi)回顾：60°第二页，共21页。\n在正方形ABCD中，E、F分别(fēnbié)是BC、CD上的点，且∠EAF＝45°，探究BE、DF、EF三条线段之间的数量关系.探究(tànjiū)：—————————————————————————————————第三页，共21页。\nE′45°FCABDE213结论(jiélùn)：EF=BE+DF第四页，共21页。\nF′45°FCABDE213结论(jiélùn)：EF=BE+DF第五页，共21页。\n（1）如图，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是BC、CD上的点，且，BE、DF、EF三条线段之间的数量关系是否(shìfǒu)仍然成立,请证明。变式：—————————————————————————————————————————第六页，共21页。\nDABCEFE′213结论(jiélùn)：EF=BE+DF第七页，共21页。\nDABCEFE′213结论(jiélùn)：EF=BE+DF第八页，共21页。\n（2）如图，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，且，BE、DF、EF三条线段之间的数量(shùliàng)关系是否仍然成立？变式：———————————————————————————————————————————第九页，共21页。\nFEDCBAE′123结论(jiélùn)：EF=BE+DF第十页，共21页。\n(3)如图，在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E、F分别是BC、CD延长线上的点，且BE、DF、EF三条线段之间的数量关系是否仍然成立，若不成立，请写出它们(tāmen)之间的数量关系，并证明.变式：ABCEFD————————————————————————————————————————————————第十一页，共21页。\nABCEFDE′12结论(jiélùn)：EF=BE-DF3第十二页，共21页。\n(4)如图，在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E、F分别是CB、DC延长线上的点，且，BE、DF、EF三条线段之间的数量(shùliàng)关系是否仍然成立，若不成立，请写出它们之间的数量(shùliàng)关系，并证明.变式：FDCABE———————————————————————————————————————————————第十三页，共21页。\n１、如图，在梯形(tīxíng)ABCD中，AD∥BC（BC＞AD），∠A=90°，AB=BC=12，∠ECD=45°，若BE=4，求ED的长.DEABCx16-x4x-4作业(zuòyè)：F8——————————第十四页，共21页。\n２、（１）探究：如图，已知Rt△ABC中，∠ACB=90°,AC=BC，点D、E在斜边AB上，且∠DCE=45°,探究AD、DE、EB三条线段(xiànduàn)之间的数量关系.CADEB————————————————————作业(zuòyè)：第十五页，共21页。\nCADEＢ１２D′３结论(jiélùn)：第十六页，共21页。\nCADEＢ１２E′３结论(jiélùn)：第十七页，共21页。\n（2）变式：已知：如图，等边△ABC中，点D、E在边AB上，且∠DCE=30°，请你找出一个条件，使线段(xiànduàn)DE、AD、EB能构成一个等腰三角形，并求出此时等腰三角形顶角的度数；CABDE————————————————第十八页，共21页。\nCABDE当AD=BE时，线段(xiànduàn)DE、AD、EB能构成一个等腰三角形且顶角∠DFE为120°.结论(jiélùn)：D′第十九页，共21页。\n（3）应用(yìngyòng)：在探究问题的条件下，如果AB=10，求BD·AE的值．BCADE第二十页，共21页。\n小结(xiǎojié)：一、知识(zhīshi)与技能：2、强化关于(guānyú)利用旋转变换解决问题：1、“半角模型”特征：①共端点的等线段；②共顶点的倍半角；①旋转的目的：将分散的条件集中，隐蔽的关系显现；②旋转的条件：具有公共端点的等线段；③旋转的方法：以公共端点为旋转中心，相等的两条线段的夹角为旋转角；第二十一页，共21页。