初中数学8上函数ppt课件 25页

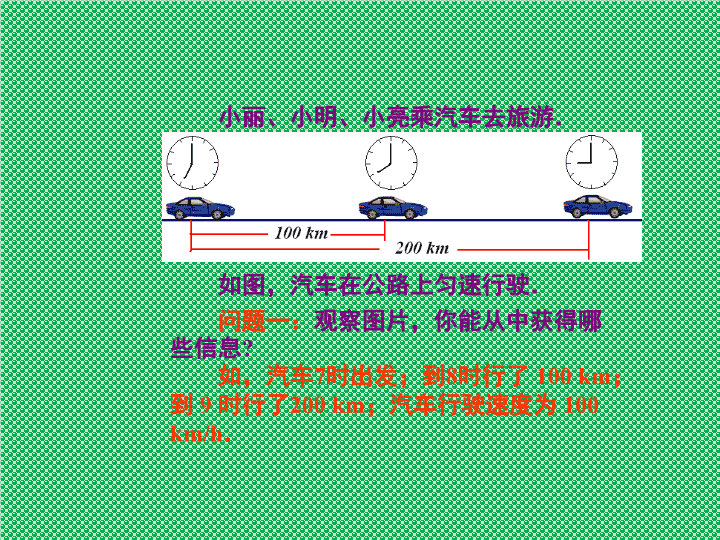
初中数学八年级上册(苏科版)5.1函数\n小丽、小明、小亮乘汽车去旅游．如图，汽车在公路上匀速行驶．问题一：观察图片，你能从中获得哪些信息?如，汽车7时出发；到8时行了100km；到9时行了200km；汽车行驶速度为100km/h．\n如图，汽车在公路上匀速行驶．问题二：如果t表示汽车行驶的时间，s表示汽车行驶的路程，想一想，在这个变化过程中有哪些常量和变量?汽车速度是常量，行驶时间t和行驶的路程s是变量．\n如图，汽车在公路上匀速行驶．小丽、小明、小亮乘汽车去旅游．问题二：如果t表示汽车行驶的时间，s表示汽车行驶的路程，想一想，在这个变化过程中有哪些常量和变量?问题三：怎样表示汽车行驶时间t和路程s的关系呢?\nＦlash动画\n如图，在这个过程中汽车在公路上匀速行驶．小丽、小明、小亮乘汽车去旅游．问题四：变量s是变量t的函数吗?由于该变化过程中有两个变量s和t，且一个变量t确定时，另一个变量s有惟一确定的值与之对应，所以这两个变量是函数关系．其中t是自变量，s是t的函数．\n函数的三种表示方法表格法：把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系的方法；关系式法：用含自变量的代数式表示函数的方法；注意：表示两个变量之间关系的式子称为函数关系式．图像法：用图像表示函数关系的方法．\n函数的图像的概念在直角坐标系中，如果描出以自变量的值为横坐标、相应函数值为纵坐标的点，那么所有这样的点组成的图形叫做这个函数的图像．\n我们知道，在太阳和月球引力的影响下，海水定时涨落的现象称为潮汐．上图就是我国某港某天的实时潮汐图（它是由仪器每隔一分钟自动记录生成的），图中的平滑曲线如实记录了当天每一时刻的潮位，揭示了这一天里潮位与时间之间的函数关系．\ns=100t从图像可以直观地看出函数的变化情况．从表格中可以直接读取数据；关系式可以全面反映整个变化过程中两变量间的关系；200400300100s/km…4321t/h···结合前面的例子，你能体会函数三种表示方法各自的好处吗?\n问题(1)他在路上花了多少时间?解：从横轴上看出，他在路上共花了7h．例1小明骑自行车从甲地到乙地，图中的折线表示小明的行程s(km)与途中所花时间t(h)之间的函数关系．\n例1小明骑自行车从甲地到乙地，图中的折线表示小明的行程s(km)与途中所花时间t(h)之间的函数关系．问题(2)折线中有一条平行于x轴的线段，试说明它的意义．解：横坐标从2变化到4时纵坐标没有变化(都是20)，说明小明在途中(距甲地20km处)滞留了2h．\n例1小明骑自行车从甲地到乙地，图中的折线表示小明的行程s(km)与途中所花时间t(h)之间的函数关系．问题(3)出发后5(h)，他离甲地有多远?解：从图上可以看出，横坐标为5时，图象上对应点的纵坐标为30，说明出发后5(h)他离甲地30(km)．\n例1小明骑自行车从甲地到乙地，图中的折线表示小明的行程s(km)与途中所花时间t(h)之间的函数关系．问题(4)你还能从图中获得哪些信息?请与同伴交流．如，从纵轴上看，全程为50(km)；图像上两条斜线段反映了在出发后至2(h)以及4(h)至7(h)内，小明所行路程随时间增加而增大；前后两时段小明的速度相同······．\n解：(1)求行驶过程中油箱内剩余油量Q(L)与行驶路程s(km)之间的函数关系式．例2汽车油箱内存油40L，每行驶100km耗油10L．\n(2)你知道汽车行驶50km，100km，200km时，油箱中剩余油量是多少吗?说说你的方法．解：当s=50时，当s=100时，当s=200时，例2汽车油箱内存油40L，每行驶100km耗油10L．\n例2汽车油箱内存油40L，每行驶100km耗油10L．(3)你认为这辆汽车现有油量够它行驶多远?解：由Q=0得，解得s=400所以最多行驶400km．\n例2汽车油箱内存油40L，每行驶100km耗油10L．(4)s的值最小取多少?s的取值范围是什么?解：根据题意可知，s的值最小取0；s的取值范围为：0≤s≤400．\n1.在一个变化过程中，自变量的取值通常有一定的范围，称为自变量的取值范围．2.对于自变量在取值范围内的一个确定值，如当x＝a时，y＝b，那么b叫当x＝a时的函数值．相关概念0≤s≤4000≤t≤７t=5时，s＝30．s=50时，Q＝35．\n练习与交流1.2m长的小棒，第一次截去一半，第二次截去剩下的一半，如此截下去······(1)第五次截去后剩下的小棒长度为m；(2)如果第n次截去后剩下的小棒长度为l，那么l=．\n练习与交流2．商店有100枝铅笔．(1)卖出10枝，还剩枝；(2)如果卖出x枝，还剩y枝，那么y=；(3)当x越来越大时，y会发生什么变化?y随x增大而减小．90100－x(4)请写出自变量取值范围．注意：在实际问题中，确定函数中自变量的取值范围时，必须使实际问题有意义．0≤x≤100且x为整数\n练习与交流3.已知函数　　　　　，写出自变量x的取值范围；(2)求当x=5时的函数值．注意：自变量的取值范围必须使含自变量的代数式有意义；求函数值的一般步骤是：①代入②计算求值(即x可取除外的所有实数)解:(1)(2)当x=5时，\n练习与交流4.从某自来水公司1995~1999年的利润图表中，你能得到哪些信息?解：由图中数据可知：95、96、97、98、99年的利润分别为：5000万元，2657.47万元，······\n问：哪几年利润(万元)下滑?哪一年盈利最多?由图象特征可知：96、99年利润下滑；(函数图像从左到右为向下趋势)97、98年利润上涨；(函数图像从左到右为向上趋势)98年盈利最多．练习与交流\n小结与反思：本节课你学到了什么？函数表示方法自变量取值范围函数值表格法关系式法图像法函数图像的概念、利用函数图像分析变量间关系