初中数学课件探究规律一 38页

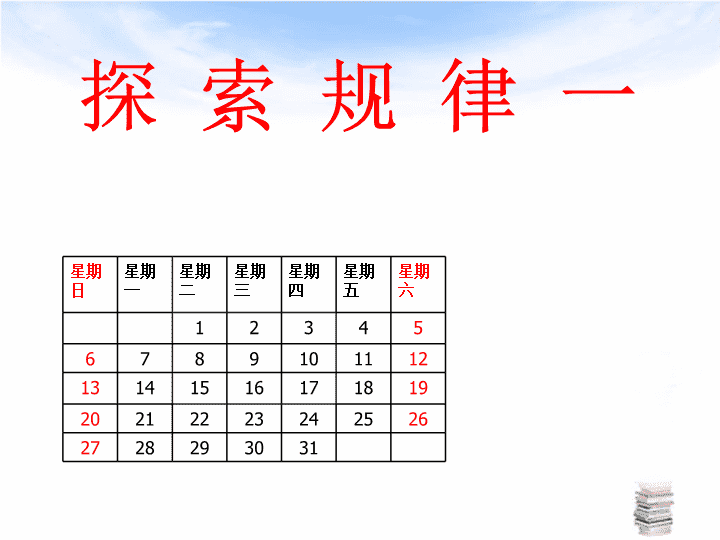
探索规律一星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031\n经历探索数量关系、运用符号表示规律、通过运算验证规律的过程。2.会用代数式表示简单问题中的数量关系，能用合并同类项、去括号等法则验证所探索的规律。3.积极思考，踊跃发言，大胆地交流你所探索的规律。学习目标\n1×9+2=1112×9+3=111123×9+4=11111234×9+5=11111………………1234567×9+8=________111111111应用规律真方便!\n这是2003年7月的日历，你能发现日历中的数字有什么规律吗?星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031\n星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031请找出同一直线上相邻数之间的关系:横行三个相邻数的关系规律一:a-1aa+1后者比前者多1能用字母表示吗?探究活动一:\n星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031规律二:aa-7a+7(2)竖列三个相邻数下者比上者多7能用字母表示吗?\n星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031(3)左上右下对角线上三个相邻数右下者比左上者多8aa+8规律三:a-8能用字母表示吗?\n星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031规律四:a-6aa+6(4)左下右上对角线上三个相邻数左下者比右上者多6能用字母表示吗?\n星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031日历中相邻三数之间有什么相等关系？规律五:同一直线上无论位置怎样的相邻三个数，首尾两数之和=2X中间数怎样用字母来表示和验证呢?探究活动二:\n(1)水平三邻数:a-1aa+1(2)竖直三邻数:aa-7a+7(3)斜下三邻数:aa+8a-8(4)斜上三邻数a-6aa+6(a-1)+(a+1)=___2a(a-7)+(a+7)=____2a(a-8)+(a+8)=____2a(a-6)+(a+6)=_____2a\n在日历中，同一直线上无论位置怎样的相邻三个数，首尾两数之和都等于中间数的2倍。注意哦!对探索到的规律既要能用文字叙述它，又要会用字母来表示和验证它!\n星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031(1)日历中3×3方框内九数之和与方框中正中间的数有何等量关系？规律六:正方形方框中九数之和=9×中间数探究活动三:\n星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031这个关系在其它方框中成立吗?规律六:九数之和=9X中间数答:成立!\n(3)这个关系对任何一个月的日历都成立吗?规律六:九数之和=9X中间数2003年2月日历日一二三四五六12345678910111213141516171819202122232425262728答:成立!\n2003年2月日历星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728(4)这个规律也能用字母表示吗?\naa-7a+8a-6a-8a+6a+7a-1a+1(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)(a+6)+(a+7)+(a+8)=______9a在正方形方框中，设中间的一个数为a，那么，其余八个数分别应怎样表示?所以，正方形方框中，九数之和等于中间数的九倍。\n(5)你还能发现正方形方框中九数之间的其它关系吗?aa-7a+8a-6a-8a+6a+7a-1a+110119171816234\n变式探究巩固提高探究活动四:\n2003年7月日历星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031变式探究(1)在+字形区域内，五个数之和与正中心何关系?能用字母表示并验证这个关系吗?答:五数之和=5×中间数aa+1a-1a+7a-7(a-1)+(a+1)+a+(a-7)+(a+7)=___5a\n2003年7月日历星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031变式探究(2)在H形区域内，七个数之和与正中心的数有关系?能用字母表示吗?答:七数之和=7×中间数aa-1a+1a-8a+6a-6a+8(a-8)+(a+8)+(a-1)+(a+1)+a+(a-6)+(a+6)=7a\n星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031星期日星期一星期二星期三星期四星期五星期六12345678910111213141516171819202122232425262728293031\n小结通过具体数值发现规律用字母来表示规律符号运算验证规律观察分析对比概括通过本节课你有收获\n操作探究(3):将一张长方形的纸对折，如右图所示可得到一条折痕。继续对折，对折时每次折痕与上次的折痕保持平行，连续对折6次后，可以得到几条折痕?如果对折10次呢?对折n次呢?要动手折叠哦?------教材第111页随堂练习\n次数折痕细胞分裂后的细胞数1234…………………n先将折叠后的结果填入下表，再与细胞分裂数作比较:细胞分裂示意图=4=2=8=1613715\n2、探索规律的一般方法：回首探究路1、探索规律的主要过程：特殊——一般——特殊(1)寻找数量关系；(2)用代数式表示规律；(3)验证规律。\n开学初，谢峥同学曾有一次惊喜地告诉我，他发现了一个规律：1×3=22–1,2×4=32–1,3×5=42–1,…你看出这个规律了吗？试试看，你能利用这个规律口算出下面结果吗？24×26=？79×81=？你还能用数学语言表示出这种规律吗？善于探索，体验成功(n-1)（n+1）=n2-124×26=252–1=624,79×81=802–1=6399\n\n1234567891011……走进游乐园活动一:请同学们伸出左手,从大拇指开始象左边显示的这只手那样数数字1,2,3……想一想\n1、数到20时，刚好落在哪个手指上？2、数到200时又会落在哪个手指上呢？2000呢?想一想？\n观察下表，按数数的方法填写下表大拇指食指中指无名指小指12345一展身手\n观察下表，你能解释数的数字与手指的对应关系吗？大拇指食指中指无名指小指1234598761011121317161514………………总结方法:除了第一排5个数字以外，其它的按从右到左再至右的顺序，是8个数一组，故我们只需把要数的数字减去5，再除以8，将得到的余数从无名指开始向左数再向右数就可以了，比如：数2000，先计算（2000－5）÷8＝249…3，我只需从无名指开始向左数3就可以了，即为食指.一展身手\n再进演练场1、完成表格内容:类别四棱柱五棱住十棱住…n棱住顶点数棱数面数\n（1）填写下表……三角形个数12345火柴棒根数（2）照这样的规律搭下去，搭n个这样的三角形需要多少根火柴棒？2、用火柴棒按下图方式搭三角形：\n,3、瑞士中学教师巴尔末成功地从光谱数据A、B、C、D、,,……中得到巴尔末公式,从而打开了光谱奥妙的大门,按照这种规律写出的第七个数据().知识点延伸\n2．图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间的小三角形三边的中点，得到图③。图①图②图③(1)图②有个三角形；图③有个三角形。(2)按上面的方法继续下去，第10个图有个三角形，第n个图形中有个三角形（用含n的代数式表示）。图1图2图3\n本节课小结探索规律的一般步骤：猜想规律表示规律验证规律具体问题观察特例成立得出结论不成立头回新重索探\n用火柴棒按下图的方式搭三角形（2）照这样的规律搭下去，搭n个这样的三角形需要多少根火柴棒？（1）填写下表：三角形个数12345火柴棒根数搭n个这样的三角形需要(2n+1)根火柴棒311957探究1\n祝同学们学习进步！再见