高中数学常用公式和基础知识梳理复习资料 13页

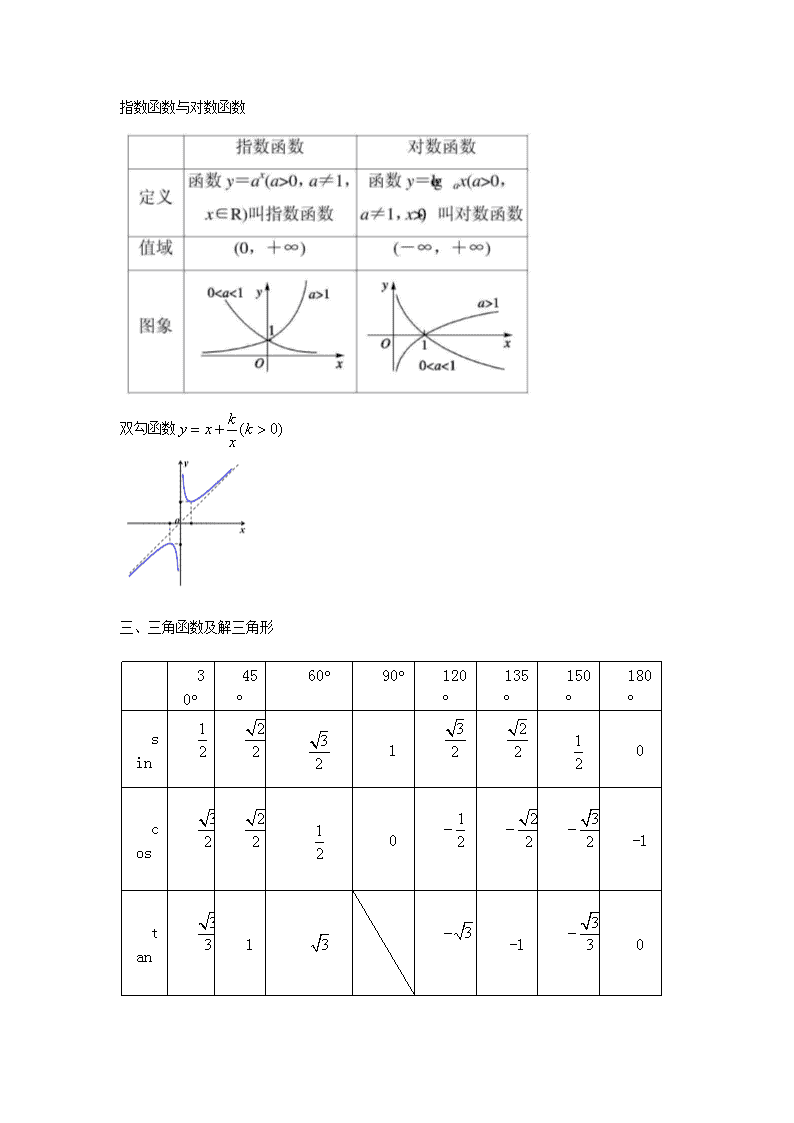
高中数学常用公式和基础知识梳理复习资料——函数篇一、集合------------------------------------------------------------------------------------------------------------------------------二、基本初等函数1、定义域：2、奇偶性：常见的奇函数：常见的偶函数：3、反函数：4、常见函数图像幂函数\n指数函数与对数函数双勾函数三、三角函数及解三角形30°45°60°90°120°135°150°180°sin10cos0-1tan1-10\n1．诱导公式对于“±α，k∈Z的三角函数值”与“α角的三角函数值”的关系可按下面口诀记忆：奇变偶不变，符号看象限．(1)“变”与“不变”是针对互余关系的函数而言的．(2)“奇”“偶”是对诱导公式k·±α中的整数k来讲的．(3)“象限”指k·±α中，将α看成锐角时，k·±α所在的象限，再根据“一全正，二正弦，三正切，四余弦”的符号规律确定原函数值的符号．2．常用三种三角函数的性质函数y＝sinxy＝cosxy＝tanx图像单调性在上单调递增；在上单调递减在[－π＋2kπ，2kπ](k∈Z)上单调递增；在[2kπ，π＋2kπ](k∈Z)上单调递减在(k∈Z)上单调递增函数y＝sinxy＝cosxy＝tanx对称性对称中心：(kπ，0)(k∈Z)；对称轴：x＝＋kπ(k∈Z)对称中心：(k∈Z)；对称轴：x＝kπ(k∈Z)对称中心：(k∈Z)3．三角函数的两种常见变换\n(1)y＝sinxy＝sin(x＋φ)y＝sin(ωx＋φ)y＝Asin(ωx＋φ)(A>0，ω>0)．(2)y＝sinxy＝sinωxy＝sin(ωx＋φ)y＝Asin(ωx＋φ)(A>0，ω>0)4．两角和差公式(1)两角和与差的正弦、余弦、正切公式①sin(α±β)＝sinαcosβ±cosαsinβ.②cos(α±β)＝cosαcosβ∓sinαsinβ.③tan(α±β)＝.[来源:学科网ZXXK](2)二倍角的正弦、余弦、正切公式①sin2α＝2sinαcosα.②cos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α.③tan2α＝.5．正余弦定理\n(边角互化：每一项边的次数都相同，则就把边化成sin；每一项的sin的次数相同，则可以把sin化成对应的边)(2)余弦定理a2＝b2＋c2－2bccosA，b2＝a2＋c2－2accosB，c2＝a2＋b2－2abcosC.推论：cosA＝，cosB＝，cosC＝.四、数列\n常用的公式证明数列是等差数列：只要证明，为常数证明数列是等比数列：只要证明，为常数——几何篇一、平面向量1、坐标运算③2、向量运算\n二、直线（1）①两点连线的斜率：；②中点：③两点间的距离：④点到直线的距离：⑤（2）两直线平行：或（3）两直线垂直：或三、圆⑴⑵:①表示圆；②圆心：；③半径：(3)直线被圆所截的弦长：（）(4)直线与圆的位置关系利用圆心到直线的距离与半径的关系①：直线与圆相离②：直线与圆相切③：直线与圆相交\n(3)切线的求法：过点P做圆的切线步骤一：先判断P是否在圆上步骤二：①若在圆上，则先求P与圆心的连线的斜率，，求，则切线方程为；②若在圆外，则设切线方程为，利用点到直线的距离求若求出的只有一个解，则另外一条切线为(4)圆与圆的位置关系(1)利用两圆心间的距离与两半径和、半径差的关系①：两圆外离②：两圆外切③：两圆相交④：两圆内含⑤：两圆为同心圆四、圆锥曲线1、椭圆（谁的分母大，焦点在哪个轴）焦点的位置焦点在x轴上焦点在y轴上图形标准方程＋＝1(a＞b＞0)＋＝1(a＞b＞0)范围－a≤x≤a且－b≤y≤b－b≤x≤b且－a≤y≤a\n顶点A1(－a,0)，A2(a,0)，B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a)，B1(－b,0)，B2(b,0)轴长短轴长＝2b，长轴长＝2a焦点F1(－c,0)，F2(c,0)F1(0，－c)，F2(0，c)焦距|F1F2|＝2c对称性对称轴x轴和y轴，对称中心(0,0)离心率e＝(0