高中数学必修一-第二章-基本初等函数(Ⅰ)-复习资料 17页

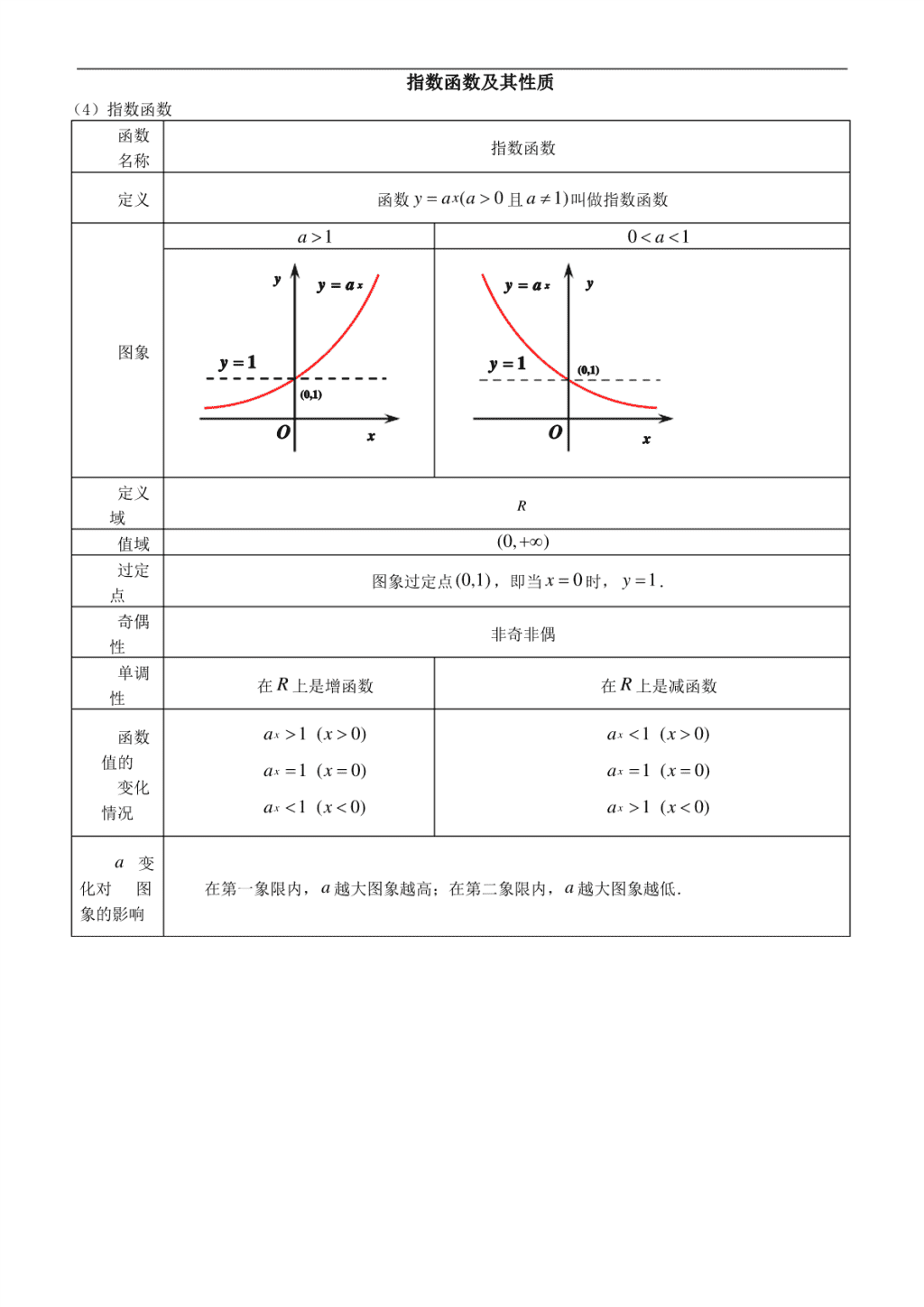
基本初等函数(Ⅰ)指数函数指数与指数幂的运算（1）根式的概念①如果xna,aR,xR,n1，且nN，那么x叫做a的n次方根．当n是奇数时，a的n次方根用符号na表示；当n是偶数时，正数a的正的n次方根用符号na表示，负的n次方根用符号na表示；0的n次方根是0；负数a没有n次方根．②式子na叫做根式，这里n叫做根指数，a叫做被开方数．当n为奇数时，a为任意实数；当n为偶数时，a0．a(a0)③根式的性质：(na)na；当n为奇数时，nana；当n为偶数时，nan|a|．a(a0)（2）分数指数幂的概念m①正数的正分数指数幂的意义是：annam(a0,m,nN,且n1)．0的正分数指数幂等于0．m1m1②正数的负分数指数幂的意义是：an()nn()m(a0,m,nN,且n1)．0的负分数指aa数幂没有意义．注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①arasars(a0,r,sR)②(ar)sars(a0,r,sR)③(ab)rarbr(a0,b0,rR)\n指数函数及其性质（4）指数函数函数指数函数名称定义函数yax(a0且a1)叫做指数函数a10a1yyaxyaxy图象y1y1(0,1)(0,1)OxOx定义R域值域(0,)过定图象过定点(0,1)，即当x0时，y1．点奇偶非奇非偶性单调在R上是增函数在R上是减函数性函数ax1(x0)ax1(x0)值的ax1(x0)ax1(x0)变化ax1(x0)ax1(x0)情况a变化对图在第一象限内，a越大图象越高；在第二象限内，a越大图象越低．象的影响\n对数函数对数与对数运算（1）对数的定义①若axN(a0,且a1)，则x叫做以a为底N的对数，记作xlogN，其中a叫做底数，Na叫做真数．②负数和零没有对数．③对数式与指数式的互化：xlogNaxN(a0,a1,N0)．a（2）几个重要的对数恒等式log10，loga1，logabb．aaa（3）常用对数与自然对数常用对数：lgN，即logN；自然对数：lnN，即logN（其中e2.71828…）．10e（4）对数的运算性质如果a0,a1,M0,N0，那么①加法：logMlogNlog(MN)aaaM②减法：logMlogNlogaaaN③数乘：nlogMlogMn(nR)aa④alogaNNn⑤logMnlogM(b0,nR)abbalogN⑥换底公式：logNb(b0,且b1)alogab\n对数函数及其性质（5）对数函数函数对数函数名称定义函数ylogx(a0且a1)叫做对数函数aa10a1x1x1yylogxyylogxaa图象(1,0)O(1,0)xOx定义(0,)域值域R过定图象过定点(1,0)，即当x1时，y0．点奇偶非奇非偶性单调在(0,)上是增函数在(0,)上是减函数性函数logx0(x1)logx0(x1)aa值的logx0(x1)logx0(x1)aa变化logx0(0x1)logx0(0x1)情况aaa变化对在第一象限内，a越大图象越靠低；在第四象限内，a越大图象越靠高．图象的影响(6)反函数的概念设函数yf(x)的定义域为A，值域为C，从式子yf(x)中解出x，得式子x(y)．如果对于y在C中的任何一个值，通过式子x(y)，x在A中都有唯一确定的值和它对应，那么式子x(y)表示x是y的函数，函数x(y)叫做函数yf(x)的反函数，记作xf1(y)，习惯上改写成yf1(x)．（7）反函数的求法①确定反函数的定义域，即原函数的值域；②从原函数式yf(x)中反解出xf1(y)；\n③将xf1(y)改写成yf1(x)，并注明反函数的定义域．（8）反函数的性质①原函数yf(x)与反函数yf1(x)的图象关于直线yx对称．②函数yf(x)的定义域、值域分别是其反函数yf1(x)的值域、定义域．③若P(a,b)在原函数yf(x)的图象上，则P'(b,a)在反函数yf1(x)的图象上．④一般地，函数yf(x)要有反函数则它必须为单调函数．幂函数（1）幂函数的定义一般地，函数yx叫做幂函数，其中x为自变量，是常数．（2）幂函数的图象（3）幂函数的性质①图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象．幂函数是偶函数时，图象分布在第一、二象限(图象关于y轴对称)；是奇函数时，图象分布在第一、三象限(图象关于原点对称)；是非奇非偶函数时，图象只分布在第一象限．②过定点：所有的幂函数在(0,)都有定义，并且图象都通过点(1,1)．③单调性：如果0，则幂函数的图象过原点，并且在[0,)上为增函数．如果0，则幂函数的图象在(0,)上为减函数，在第一象限内，图象无限接近x轴与y轴．q④奇偶性：当为奇数时，幂函数为奇函数，当为偶数时，幂函数为偶函数．当（其中p,qp\nqq互质，p和qZ），若p为奇数q为奇数时，则yxp是奇函数，若p为奇数q为偶数时，则yxp是q偶函数，若p为偶数q为奇数时，则yxp是非奇非偶函数．⑤图象特征：幂函数yx,x(0,)，当1时，若0x1，其图象在直线yx下方，若x1，其图象在直线yx上方，当1时，若0x1，其图象在直线yx上方，若x1，其图象在直线yx下方．补充知识---二次函数（1）二次函数解析式的三种形式①一般式：f(x)ax2bxc(a0)②顶点式：f(x)a(xh)2k(a0)③两根式：f(x)a(xx)(xx)(a0)12（2）求二次函数解析式的方法①已知三个点坐标时，宜用一般式．②已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式．③若已知抛物线与x轴有两个交点，且横线坐标已知时，选用两根式求f(x)更方便．（3）二次函数图象的性质b①二次函数f(x)ax2bxc(a0)的图象是一条抛物线，对称轴方程为x,顶点坐标是2ab4acb2(,)．2a4abbb②当a0时，抛物线开口向上，函数在(,]上递减，在[,)上递增，当x时，2a2a2a4acb2bbf(x)；当a0时，抛物线开口向下，函数在(,]上递增，在[,)上递减，min4a2a2ab4acb2当x时，f(x)．2amax4a③二次函数f(x)ax2bxc(a0)当b24ac0时，图象与x轴有两个交点M(x,0),M(x,0),|MM||xx|．11221212|a|（4）二次函数f(x)ax2bxc(a0)在闭区间[p,q]上的最值1设f(x)在区间[p,q]上的最大值为M，最小值为m，令x(pq)．02（Ⅰ）当a0时（开口向上）\n最小值bbb①若p，则mf(p)②若pq，则mf()2a2a2afff(p)(q)(q)OxOxfbbf()f((p))2a2ab③若q，则mf(q)2af(p)Oxfbf()2a(q)最大值bb①若x，则Mf(q)②x，则Mf(p)2a02a0ffx(q)(p)xg0g0OxOxffbbf()f((p))2a2a(q)(Ⅱ)当a0时(开口向下)\n最大值bbb①若p，则Mf(p)②若pq，则Mf()2a2a2abbf()f()2a2aff(p)(p)OxOxff(q)(q)b③若q，则Mf(q)2abff()2a(q)Oxf(p)最小值bb①若x，则mf(q)②x，则mf(p)．2a02a0bbf()ff()2a2af(q)(p)xxg00gOxOxff(q)(p)指数与指数幂的运算¤学习目标：理解有理指数幂的含义，通过具体实例了解实数指数幂的意义，掌握根式与分数指数幂的互化，掌握有理数指数幂的运算.¤知识要点：1.若xna，则x叫做a的n次方根，记为na，其中n>1，且nN.n次方根具有如下性质：（1）在实数范围内，正数的奇次方根是一个正数，负数的奇次方根是一个负数；正数的偶次方根是两个绝对值相等、符号相反的数，负数的偶次方根没有意义；零的任何次方根都是零.（2）n次方根（n1,且nN*）有如下恒等式：a,n为奇数(na)na；nan；npampnam，（a0）.|a|,n为偶数\nmm112.规定正数的分数指数幂：annam（a0,m,nN,且n1）；an.mnaman¤例题精讲：【例1】求下列各式的值：（1）n（3）n（n1,且nN*）；（2）(xy)2.解：（1）当n为奇数时，n（3）n3；当n为偶数时，n（3）n|3|3.（2）(xy)2|xy|.当xy时，(xy)2xy；当xy时，(xy)2yx.a3na3n【例2】已知a2n21，求的值.anana3na3n(anan)(a2n1a2n)1解：a2n1a2n211221.anananan21211115a3b23ab224【例3】化简：（1）(2a3b2)(6a2b3)(3a6b6)；（2）（a＞0，b＞0）；（3）8193.11b(a4b2)43a211115解：（1）原式=[2(6)(3)]a326b2364ab04a.311311104a2b[(ab2)3]2a2ba6b3a6b3a（2）原式====.12727bab2(b/a)3a3b3a3b32121221121144232442444（3）原式=3[(3)]33323433(3433)4(3)(33)4336363.点评：根式化分数指数幂时，切记不能混淆，注意将根指数化为分母，幂指数化为分子，根号的嵌套，化为幂的幂.正确转化和运用幂的运算性质，是复杂根式化简的关键.【例4】化简与求值：1111（1）642642；（2）.1335572n12n1解：（1）原式=22222(2)222222(2)2=(22)2(22)2=2222=4.3153752n12n1（2）原式=315375(2n1)(2n1)11=(3153752n12n1)=(2n11).22点评：形如AB的双重根式，当A2B是一个平方数时，则能通过配方法去掉双重根号，这也是双重根号能否开方的判别技巧.而分母有理化中，常常用到的是平方差公式，第2小题也体现了一种消去法的思想.第（1）小题还可用平方法，即先算得原式的平方，再开方而得.指数函数及其性质（一）¤学习目标：理解指数函数的概念和意义，能借助计算器或计算机画出具体指数函数的图像，探索并理解指数函数的单调性与特殊点，掌握指数函数的性质.¤知识要点：1.定义：一般地，函数yax(a0,且a1)叫做指数函数（exponentialfunction），其中x是自变量，函数的定义域为R.12.以函数y2x与y()x的图象为例，观察这一对函数的图象，可总结出如下2性质：定义域为R，值域为(0,)；当x0时，y1，即图象过定点(0,1)；当0a1\n时，在R上是减函数，当a1时，在R上是增函数.¤例题精讲：【例1】求下列函数的定义域：1110x100（1）y23x；（2）y()5x；（3）y.310x1001解：（1）要使y23x有意义，其中自变量x需满足3x0，即x3.∴其定义域为{x|x3}.1（2）要使y()5x有意义，其中自变量x需满足5x0，即x5.∴其定义域为{x|x5}.310x100（3）要使y有意义，其中自变量x需满足10x1000，即x2.∴其定义域为{x|x2}.10x100【例2】求下列函数的值域：12（1）y()3x1；（2）y4x2x132121解：（1）观察易知0，则有y()3x1()01.∴原函数的值域为{y|y0,且y1}.3x13313（2）y4x2x1(2x)22x1.令t2x，易知t0.则yt2t1(t)2.2413结合二次函数的图象，由其对称轴观察得到y(t)2在t0上为增函数，241313所以y(t)2(0)21.∴原函数的值域为{y|y1}.2424【例3】（05年福建卷.理5文6）函数f(x)axb的图象如图，其中a、b为常数，则下列结论正确的是（）.A．a1,b0B．a1,b0C．0a1,b0D．0a1,b0解：从曲线的变化趋势，可以得到函数f(x)为减函数，从而00，即b<0.所以选D.点评：观察图象变化趋势，得到函数的单调性，结合指数函数的单调性，得到参数a的范围.根据所给函数式的平移变换规律，得到参数b的范围.也可以取x=1时的特殊点，得到ab1a0，从而b<0.【例4】已知函数f(x)a23x(a0,且a1).（1）求该函数的图象恒过的定点坐标；（2）指出该函数的单调性.2解：（1）当23x0，即x时，a23xa01.32所以，该函数的图象恒过定点(,1).3（2）∵u23x是减函数，∴当0a1时，f(x)在R上是增函数；当a1时，f(x)在R上是减函数.点评：底数两种情况的辨析，实质就是分类讨论思想的运用.而含参指数型函数的研究，要求正确处理与参数相关的变与不变.指数函数及其性质（二）¤学习目标：在解决简单实际问题的过程中，体会指数函数是一类重要的函数模型.掌握指数函数的性质及应用.¤知识要点：1以函数y2x与y()x的图象为例，得出这以下结论：2（1）函数yf(x)的图象与yf(x)的图象关于y轴对称.（2）指数函数yax(a0,且a1)的图象在第一象限内，图象由下至上，底数由小到大.¤例题精讲：【例1】按从小到大的顺序排列下列各数：32，0.32，22，0.22.\n解：构造四个指数函数，分别为y3x，y0.3x，y2x，y0.2x，它们在第一象限内，图象由下至上，依次是y0.2x，y0.3x，y2x，y3x.如右图所示.由于x20，所以从小到大依次排列是：0.22，0.32，22，32.点评：利用指数函数图象的分步规律，巧妙地解决了同指数的幂的大小比较问题.当然，我们在后面的学习中，可以直接利用幂函数的单调性来比较此类大小.2x1【例2】已知f(x).（1）讨论f(x)的奇偶性；（2）讨论f(x)的单调性.2x1解：（1）f(x)的定义域为R.2x1(2x1)g2x12x2x1∵f(x)f(x).2x1(2x1)g2x12x2x1∴f(x)为奇函数.（2）设任意x,xR，且xx，则12122x12x12(2x2x)f(x)f(x)1212.122x12x1(2x1)(2x1)1212由于xx，从而2x12x2，即2x12x20.12∴f(x)f(x)0，即f(x)f(x).∴f(x)为增函数.1212点评：在这里，奇偶性与单调性的判别，都是直接利用知识的定义来解决.需要我们理解两个定义，掌握其运用的基本模式，并能熟练的进行代数变形，得到理想中的结果.1【例3】求下列函数的单调区间：（1）yax22x3；（2）y.0.2x1解：（1）设yau,ux22x3.由ux22x3(x1)24知，u在(,1]上为减函数，在[1,)上为增函数.根据yau的单调性，当a1时，y关于u为增函数；当0a1时，y关于u为减函数.∴当a1时，原函数的增区间为[1,)，减区间为(,1]；当0a1时，原函数的增区间为(,1]，减区间为[1,).1（2）函数的定义域为{x|x0}.设y,u0.2x.易知u0.2x为减函数.u11而根据y的图象可以得到，在区间(,1)与(1,)上，y关于u均为减函数.u1∴在(,0)上，原函数为增函数；在(0,)上，原函数也为增函数.点评：研究形如yaf(x)(a0，且a1)的函数的单调性，可以有如下结论：当a1时，函数yaf(x)的单调性与f(x)的单调性相同；当0a1时，函数yaf(x)的单调性与f(x)的单调性相反.而对于形如y(ax)(a0，且a1)的函数单调性的研究，也需结合ax的单调性及(t)的单调性进行研究.复合函数yf((x))的单调性研究，遵循一般步骤和结论，即：分别求出yf(u)与u(x)两个函数的单调性，再按口诀“同增异减”得出复合后的单调性，即两个函数同为增函数或者同为减函数，则复合后结果为增函数；若两个函数一增一减，则复合后结果为减函数.为何有“同增异减”？我们可以抓住“x的变化→u(x)的变化→yf(u)的变化”这样一条思路进行分析.对数与对数运算（一）¤学习目标：理解对数的概念；能够说明对数与指数的关系；掌握对数式与指数式的相互转化，并能运用指对互化关系研究一些问题.¤知识要点：1.定义：一般地，如果axN(a0,a1)，那么数x叫做以a为底N的对数（logarithm）.记作xlogN，a其中a叫做对数的底数，N叫做真数2.我们通常将以10为底的对数叫做常用对数（commonlogarithm），并把常用对数logN简记为lgN在科10学技术中常使用以无理数e=2.71828……为底的对数，以e为底的对数叫自然对数，并把自然对数logN简记作lnNe3.根据对数的定义，得到对数与指数间的互化关系：当a0,a1时，logNbabN.a\n4.负数与零没有对数；log10，loga1aa¤例题精讲：【例1】将下列指数式化为对数式，对数式化为指数式：1（1）27；（2）3a27；（3）1010.1；128（4）log325；（5）lg0.0013；（6）ln100=4.606.121解：（1）log7；（2）log27a；（3）lg0.11；212831（4）()532；（5）1030.001；（6）e4.606100.2【例2】计算下列各式的值：（1）lg0.001；（2）log8；（3）lne.4解：（1）设lg0.001x，则10x0.001，即10x103，解得x3.所以，lg0.0013.33（2）设log8x，则4x8，即22x23，解得x.所以，log8.4242111（3）设lnex，则exe，即exe2，解得x.所以，lne.22M【例3】求证：（1）logann；（2）logMlogNlog.aaaaN证明：（1）设loganx，则anax，解得xn.a所以logann.a（2）设logMp，logNq，则apM，aqN.aaMapM因为apq，则logpqlogMlogN.NaqaNaaM所以，logMlogNlog.aaaN点评：对数运算性质是对数运算的灵魂，其推导以对数定义得到的指对互化关系为桥梁，结合指数运算的性质而得到.我们需熟知各种运算性质的推导.logb【例4】试推导出换底公式：logbc（a0，且a1；c0，且c1；b0）.alogac证明：设logbm，logan，logbp，cca则cmb，cna，apb.从而(cn)pbcm，即npm.m由于nlogalog10，则p.ccnlogb所以，logbc.alogac点评：换底公式是解决对数运算中底数不相同时的核心工具.其推导也密切联系指数运算性质，牢牢扣住指对互化关系.对数与对数运算（二）¤学习目标：通过阅读材料，了解对数的发现历史以及对简化运算的作用；理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；理解推导这些运算性质的依据和过程；能较熟练地运用运算性质解决问题.¤知识要点：M1.对数的运算法则：log(MgN)logMlogN，loglogMlogN，logMnnlogM，其中aaaaNaaaaa0,且a1，M0,N0,nR.三条法则是有力的解题工具，能化简与求值复杂的对数式.logN12.对数的换底公式logNb.如果令b=N，则得到了对数的倒数公式logb.同样，也可以推alogaalogabb\nn导出一些对数恒等式，如logNnlogN，logNnlogN，logbglogcgloga1等.anaammaabc¤例题精讲：1【例1】化简与求值：（1）(lg2)2lg2glg5(lg2)2lg21；（2）log(4747).221111解：（1）原式=(lg2)2lg2glg5(lg21)2=lg22lg2glg5(lg21)22421111=lg22lg2glg5lg21=lg2(lg22lg52)142241=lg2(lg1002)1011.4112（2）原式=log(4747)2=log(4747)222211=log(47472427)=log14.222211【例2】若2a5b10，则=.（教材P83B组2题）ab解：由2a5b10，得alog10，blog10.则251111lg2g5lg101.ablog10log1025【例3】（1）方程lgxlg(x3)1的解x=________；（2）设x,x是方程lg2xalgxb0的两个根，则xgx的值是.1212解：（1）由lgxlg(x3)1，得lg[x(x3)]lg10，即x(x3)10，整理为x23x100.解得x=－5或x=2.∵x＞0，∴x=2.（2）设lgxt，则原方程化为t2atb0，其两根为tlgx,tlgx.1122由ttlgxlgxlg(xgx)blg10b，得到xgx10b.12121212点评：同底法是解简单对数方程的法宝，化同底的过程中需要结合对数的运算性质.第2小题巧妙利用了换元思想和一元二次方程根与系数的关系.111【例4】（1）化简：；log7log7log7532（2）设log3glog4glog5gglog2006glogm4，求实数m的值.23420052006解：（1）原式=log5log3log2log(532)log30.77777log4log5log2006logm（2）原式左边=log3g2g2gg2g2logm,2log3log4log2005log200622222∴logm4log24，解得m16.22点评：换底时，一般情况下可以换为任意的底数，但习惯于化为常用对数.换底之后，注意结合对数的运算性质完成后阶段的运算.对数函数及其性质（一）¤学习目标：通过具体实例，直观了解对数函数模型所刻画的数量关系，初步理解对数函数的概念，体会对数函数是一类重要的函数模型；能借助计算器或计算机画出具体对数函数的图像，探索并了解对数函数的单调性与特殊点.¤知识要点：1.定义：一般地，当a＞0且a≠1时，函数y=logx叫做对数函数(logarithmicfunction).自变量是x；函数a的定义域是（0，+∞）.2.由ylogx与ylogx的图象，可以归纳出对数函数的性质：定义域为(0,)，值域为R；当x1时，212y0，即图象过定点(1,0)；当0a1时，在(0,)上递减，当a1时，在(0,)上递增.\n¤例题精讲：1【例1】比较大小：（1）log0.8，log0.7，log0.9；（2）log2，log3，log.0.90.90.83243解：（1）∵ylogx在(0,)上是减函数，且0.90.80.7，∴1log0.8log0.7.0.90.90.9又log0.9log0.81，所以log0.9log0.8log0.7.0.80.80.80.90.9（2）由log1log2log3，得0log21.33331又log3log21，loglog10，224341所以loglog2log3.4332【例2】求下列函数的定义域：（1）ylog(3x5)；（2）ylog(4x)3.20.5解：（1）由log(3x5)0log1，得3x51，解得x2.22所以原函数的定义域为[2,).（2）由log(4x)30，即log(4x)3log0.53，0.50.50.511所以04x0.53，解得0x.所以，原函数的定义域为(0,].3232【例3】已知函数f(x)log(x3)的区间[2,1]上总有|f(x)|2，求实数a的取值范围.a解：∵x[2,1]，∴1x32当a1时，log1log(x3)log2，即0f(x)log2.aaaaa1∵|f(x)|2，∴，解得a2.log22a当0a1时，log2log(x3)log1，即log2f(x)0.aaaa0a12∵|f(x)|2，∴，解得0a.log222a2综上可得，实数a的取值范围是(0,)U(2,).2点评：先对底数a分两种情况讨论，再利用函数的单调性及已知条件，列出关于参数a的不等式组，解不等式（组）而得到参数的范围.解决此类问题的关键是合理转化与分类讨论，不等式法求参数范围.【例4】求不等式log(2x7)log(4x1)(a0,且a1)中x的取值范围.aa2x701解：当a1时，原不等式化为4x10，解得x4.42x74x12x70当0a1时，原不等式化为4x10，解得x4.2x74x11所以，当a1时，x的取值范围为(,4)；当0a1时，x的取值范围为(4,).4点评：结合单调性，将对数不等式转化为熟悉的不等式组，注意对数式有意义时真数大于0的要求.当底数a不确定时，需要对底数a分两种情况进行讨论.对数函数及其性质（二）¤学习目标：掌握对数函数的性质，并能应用对数函数解决实际中的问题.知道指数函数y=ax与对数函数y=logx互为反函数.（a>0,a≠1）a¤知识要点：1.当一个函数是一一映射时,可以把这个函数的因变量作为一个新函数的自变量,而把这个函数的自变量新的函数的因变量.我们称这两个函数为反函数（inversefunction）.互为反函数的两个函数的图象关于直线yx对称.2.函数yax(a0,a1)与对数函数ylogx(a0,a1)互为反函数.a3.复合函数yf((x))的单调性研究，口诀是“同增异减”，即两个函数同增或同减，复合后结果为增函数；\n若两个函数一增一减，则复合后结果为减函数.研究复合函数单调性的具体步骤是：（i）求定义域；（ii）拆分函数；（iii）分别求yf(u),u(x)的单调性；（iv）按“同增异减”得出复合函数的单调性.¤例题精讲：【例1】讨论函数ylog(32x)的单调性.0.333解：先求定义域，由32x0,解得x.设t32x,x(,)，易知为减函数.223又∵函数ylogt是减函数，故函数ylog(32x)在(,)上单调递增.0.30.32【例2】（05年山东卷.文2）下列大小关系正确的是（）.A.0.4330.4log0.3B.0.43log0.330.444C.log0.30.4330.4D.log0.330.40.4344解：在同一坐标系中分别画出y0.4x,y3x,ylogx的图象，分别作出当自变量x取3，0.4，0.3时的函数4值.观察图象容易得到：log0.30.4330.4.故选C.4【例3】指数函数yax(a0,a1)的图象与对数函数ylogx(a0,a1)的图象有何关系？a解：在指数函数yax的图象上任取一点M(x,y)，则yax0.000由指对互化关系，有logyx.a00所以，点M'(y,x)在对数函数ylogx的图象上.00a因为点M(x,y)与点M'(y,x)关于直线yx对称，0000所以指数函数yax(a0,a1)的图象与对数函数ylogx(a0,a1)的图象关于直线yx对称.a点评：两个函数的对称性，由任意点的对称而推证出来.这种对称性实质是反函数的图象特征，即函数yax与ylogx(a0,a1)互为反函数，而互为反函数的两个函数图象关于直线yx对称.a【例4】2005年10月12日，我国成功发射了“神州”六号载人飞船，这标志着中国人民又迈出了具有历史意义的一步.已知火箭的起飞重量M是箭体（包括搭载的飞行器）的重量m和燃料重量x之和.在不考虑空气阻力的条件下，假设火箭的最大速度y关于x的函数关系式为：yk[ln(mx)ln(2m)]4ln2(其中k0).当燃料重量为(e1)m吨（e为自然对数的底数，e2.72）时，该火箭的最大速度为4（km/s）.（1）求火箭的最大速度y(km/s)与燃料重量x吨之间的函数关系式yf(x)；（2）已知该火箭的起飞重量是544吨，是应装载多少吨燃料，才能使该火箭的最大飞行速度达到8km/s，顺利地把飞船发送到预定的轨道？解：（1）依题意把x(e1)m,y4代入函数关系式yk[ln(mx)ln(2m)]4ln2，解得k8.mx所以所求的函数关系式为y8[ln(mx)ln(2m)]4ln2,整理得yln()8.m（2）设应装载x吨燃料方能满足题意，此时，m544x,y8mx544代入函数关系式yln()8,得ln1,解得x344(吨).m544x所以，应装载344吨燃料方能顺利地把飞船发送到预定的轨道.点评：直接给定参数待定的函数模型时，由待定系数法的思想，代入已知的数据得到相关的方程而求得待定系数.一般求出函数模型后，还利用模型来研究一些其它问题.代入法、方程思想、对数运算，是解答此类问题的方法精髓.幂函数¤学习目标：通过实例，了解幂函数的概念；结合函数y=x,y=x2,y=x3,y=1/x,y=x1/2的图像，了解它们的变化情况.知识要点：\n1.幂函数的基本形式是yx，其中x是自变量，是常数.要求掌握yx，yx2，yx3，yx1/2，yx1这五个常用幂函数的图象.2.观察出幂函数的共性，总结如下：（1）当0时，图象过定点(0,0),(1,1)；在(0,)上是增函数（.2）当0时，图象过定点(1,1)；在(0,)上是减函数；在第一象限内，图象向上及向右都与坐标轴无限趋近.3.幂函数yx的图象，在第一象限内，直线x1的右侧，图象由下至上，指数由小到大.y轴和直线x1之间，图象由上至下，指数由小到大.¤例题精讲：【例1】已知幂函数yf(x)的图象过点(27,3)，试讨论其单调性.1解：设yx，代入点(27,3)，得327，解得，31所以yx3，在R上单调递增.【例2】已知幂函数yxm6(mZ)与yx2m(mZ)的图象都与x、y轴都没有公共点，且yxm2(mZ)的图象关于y轴对称，求m的值．m60解：∵幂函数图象与x、y轴都没有公共点，∴，解得2m6.2m0又∵yxm2(mZ)的图象关于y轴对称，∴m2为偶数，即得m4.【例3】幂函数yxm与yxn在第一象限内的图象如图所示，则（）.A．1n0m1B．n1,0m1C．1n0,m1D．n1,m1解：由幂函数图象在第一象限内的分布规律，观察第一象限内直线x1的右侧，图象由下至上，依次是yxn，yx1，yx0，yxm，yx1，所以有n10m1.选B.点评：观察第一象限内直线x1的右侧，结合所记忆的分布规律.注意比较两个隐含的图象yx1与yx0.【例4】本市某区大力开展民心工程，近几年来对全区am2的老房子进行平改坡（“平改坡”是指在建筑结构许可条件下，将多层住宅平屋面改建成坡屋顶，并对外墙面进行整修粉饰，达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为），且每年平改坡面积的百分比相等.若改造到面积的一半时，所用时间需10年.已知到今年2为止，平改坡剩余面积为原来的.2（1）求每年平改坡的百分比；（2）问到今年为止，该平改坡工程已进行了多少年？a（3）若通过技术创新，至少保留m2的老房子开辟新的改造途径.今后最多还需平改坡多少年？4解：（1）设每年平改坡的百分比为x(0x1)，则11111a(1x)10a，即1x()10，解得x1()100.06706.70.22221n11（2）设到今年为止，该工程已经进行了n年，则a(1x)na，即()10()2，解得n=5.222所以，到今年为止，该工程已经进行了5年.11m51（3）设今后最多还需平改坡m年，则a(1x)m5a，即()10()2，解得m=15.422所以，今后最多还需平改坡15年.\n点评：以房屋改造为背景，从中抽象出函数模型，结合两组改造数据及要求，通过三个等式求得具有实际意义的底数或指数.体现了代入法、方程思想等数学方法的运用.基本初等函数（Ⅰ）复习¤学习目标：理解掌握指数函数、对数函数和幂函数的性质、图象及运算性质.突出联系与转化、分类与讨论、数与形结合等重要的数学思想、能力.通过对指数函数、对数函数等具体函数的研究，加深对函数概念的理解.¤例题精讲：xxf(x)f(x)【例1】若f(x)ax(a0,且a1)，则f(12)12.22f(x)f(x)xxaxaxx1x2axax2axax(axax)212121212证明：12f(12)a20.22222xxf(x)f(x)∴f(12)12.（注：此性质为函数的凹凸性）22bx【例2】已知函数f(x)(b0,a0).ax2111（1）判断f(x)的奇偶性；（2）若f(1),log(4ab)log4，求a，b的值.2322bx解：（1）f(x)定义域为R，f(x)f(x)，故f(x)是奇函数.ax21b1（2）由f(1)，则a2b10.又log(4a-b)=1，即4a-b=3.3a12a2b10由得a=1，b=1.4ab3exa【例3】（01天津卷.19）设a＞0，f(x)是R上的偶函数.aex（1）求a的值；（2）证明f(x)在(0,)上是增函数．exa解：（1）∵f(x)是R上的偶函数，∴f(x)f(x)0.aexexaexa111∴0(a)ex(a)ex0(a)(exex)0.aexaexaaa1ex－e-x不可能恒为“0”，∴当－a＝0时等式恒成立，∴a＝1．a（2）在(0,)上任取x＜x，12ex11111f(x)f(x)ex(exex)()(exex)(1)2121212aexexexexexex121212(exex)(exex1)1212∵e＞1，x＜x，∴ex1ex21，∴ex1ex2＞1，＜0，12exex12∴f(x)f(x)0，∴f(x)是在(0,)上的增函数．12点评：本题主要考查了函数的奇偶性以及单调性的基础知识．此题中的函数，也可以看成指数函数yax与xaxay的复合，可以进一步变式探讨y的单调性.axax【例4】已知1992年底世界人口达到54.8亿.（1）若人口的平均增长率为1.2%，写出经过t年后的世界人口数y（亿）与t的函数解析式；（2）若人口的平均增长率为x%，写出2010年底世界人口数为y（亿）与x的函数解析式.如果要使2010年的人口数不超过66.8亿，试求人口的年平均增长率应控制在多少以内？解：（1）经过t年后的世界人口数为y54.8(11.2)t54.81.012t,tN*.（2）2010年底的世界人口数y与x的函数解析式为y54.8(1x)18.66.8由y54.8(1x)1866.8，解得x100(181)1.1.54.8所以，人口的年平均增长率应控制在1.1%以内.