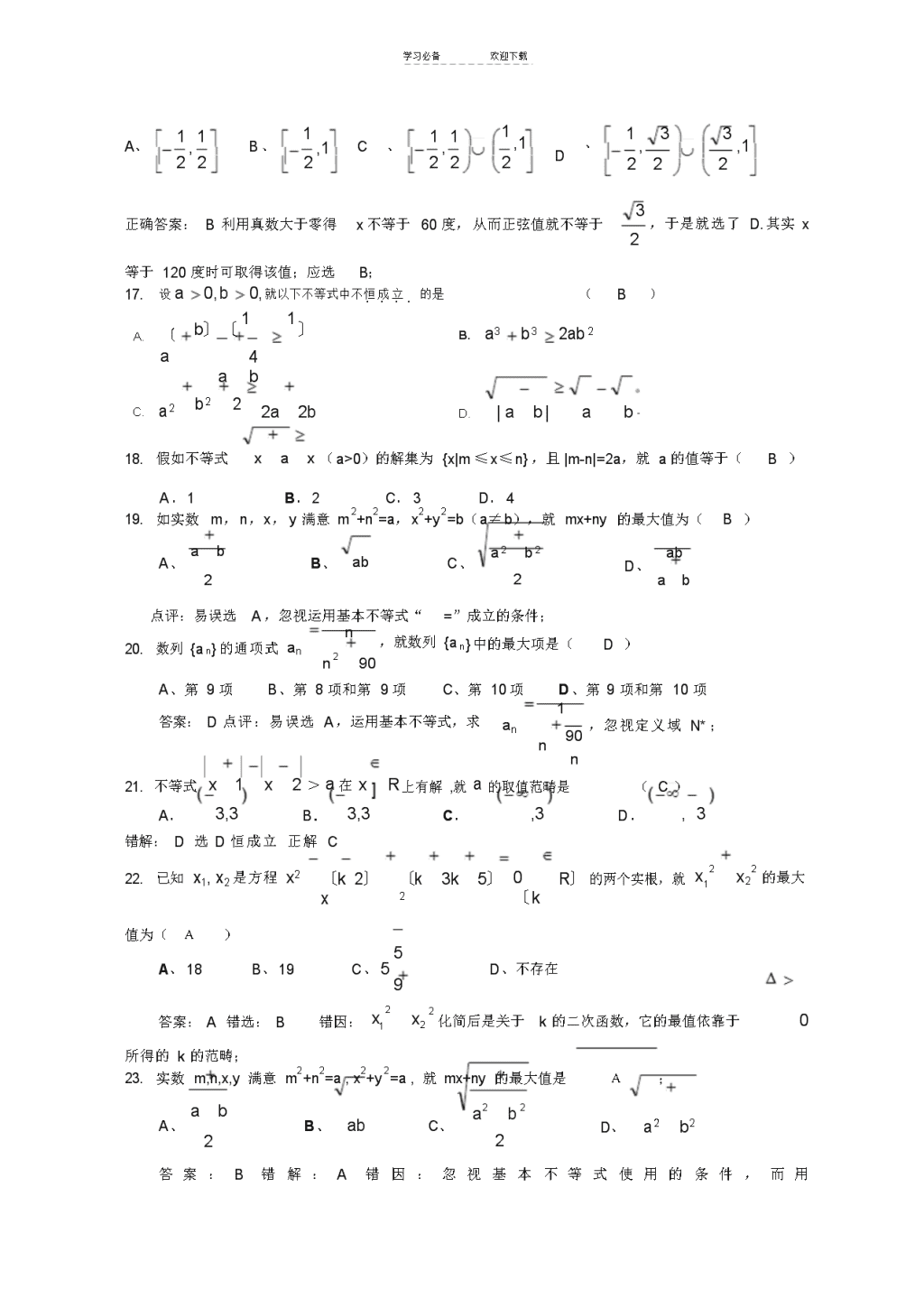- 301.61 KB
- 2022-07-28 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
学习必备欢迎下载学习必备欢迎下载一、挑选题:高中数学不等式部分错题精选学习必备欢迎下载学习必备欢迎下载1.设f〔x〕lgx,如0f〔b〕>f〔c〕,就以下结论中正确选项〔D〕学习必备欢迎下载A〔a-1〕〔c-1〕>0Bac>1Cac=1Dac<1学习必备欢迎下载错解缘由是没有数形结合意识,正解是作出函数f〔x〕lgx的图象,由图可得出选D.学习必备欢迎下载2.设x,yR,就使xy1成立的充分不必要条件是〔D〕11学习必备欢迎下载Axy1Bx或yCx1Dx<-1学习必备欢迎下载22错解:选B,对充分不必要条件的概念懂得不清,“或”与“且”概念不清,正确答案为D;学习必备欢迎下载3.不等式〔x1〕x20的解集是〔D〕学习必备欢迎下载学习必备欢迎下载A{x|x1}B{x|x1}C{x|x2且x1}D{x|x2或x1}学习必备欢迎下载错解:选B,不等式的等价转化显现错误,没考虑x=-2的情形;正确答案为D;4.某工厂第一年产量为A,其次年增长率为a,第三年增长率为b,这两年的平均增长率为x,就学习必备欢迎下载AxabB2xabC2xabD2xab2学习必备欢迎下载错解:对概念懂得不清,不能敏捷运用平均数的关系;正确答案为B;学习必备欢迎下载5.已知1ab3且2ab4,就2a+3b的取值范畴是〔D〕学习必备欢迎下载A〔13,17〕711,B〔〕713,C〔〕D〔9,13〕学习必备欢迎下载22222222错解:对条件“”不是等价转化,解出a,b范畴,再求2a+3b的范畴,扩大了范畴;正解:用待定系数法,解出2a+3b=5〔a+b〕1〔a-b〕,求出结果为D;226.如不等式ax2+x+a<0的解集为Φ,就实数a的取值范畴(D)学习必备欢迎下载Aa≤-11或a≥221Ba<211C-≤a≤221Da≥2学习必备欢迎下载正确答案:D错因:同学对一元二次不等式与二次函数的图象之间的关系仍不能把握;学习必备欢迎下载7.已知函数y=㏒1〔3x22ax5〕在[-1,+∞)上是减函数,就实数a的取值范畴()学习必备欢迎下载Aa≤-6B-60<a<-6C-8<a≤-6D-8≤a≤-6正确答案:C错因:同学遗忘考虑定义域真数大于0这一隐含条件;学习必备欢迎下载8.已知实数x、y、z满意x+y+z=0,xyz>0记T=1+x1+1,就(C)yz学习必备欢迎下载AT>0BT=0CT<0D以上皆错\n学习必备欢迎下载学习必备欢迎下载正确答案:C错因:同学对已知条件不能综合考虑,判定T的符号改为判定xyz〔1+1xy学习必备欢迎下载+1〕的符号;z1.以下四组条件中,甲是乙的充分不必要条件的是(D)学习必备欢迎下载A.甲a>b,乙1<1B甲ab<0,乙∣a+b∣<∣a-b∣学习必备欢迎下载ab0a10ab2学习必备欢迎下载C.甲a=b,乙a+b=2abD甲,乙0b11ab2学习必备欢迎下载正确答案:D错因:同学对不等式基本性质成立的条件懂得不深刻;10.f〔x〕=︱2x—1|,当a<b<c时有f〔a〕>f〔c〕>f〔b〕就(D)A学习必备欢迎下载A.a<0,b<0,c<0Ba<0,b>0,c>0C2a<2cD2a2c<2学习必备欢迎下载正确答案:D错因:同学不能应用数形结合的思想方法解题;11.a,b∈R,且a>b,就以下不等式中恒成立的是(B)学习必备欢迎下载A.a2>b2B.〔1a1b〕<〔〕22aC.lg〔a-b〕>0D.>1b学习必备欢迎下载正确答案:B;错误缘由:简单忽视不等式成立的条件;12.x为实数,不等式|x-3|-|x-1|>m恒成立,就m的取值范畴是(D)A.m>2B.m<2C.m>-2D.m<-2正确答案:D易忽视肯定值的几何意义,用常规解法又简单出错;13.已知实数x、y满意x2+y2=1,就〔1-xy〕〔1+xy〕〔B〕学习必备欢迎下载A.有最小值1,也有最大值1B.有最小值23,也有最大值14学习必备欢迎下载学习必备欢迎下载C.有最小值3,但无最大值D.有最大值1,但无最小值4学习必备欢迎下载正确答案:B错因:简单忽视x、y本身的范畴;学习必备欢迎下载14.如a>b>0,且abm>a,就m的取值范畴是()mb学习必备欢迎下载A.mRB.m>0C.m<0D.–b0)的解集为{x|m≤x≤n},且|m-n|=2a,就a的值等于(B)A.1B.2C.3D.413.如实数m,n,x,y满意m2+n2=a,x2+y2=b(a≠b),就mx+ny的最大值为(B)学习必备欢迎下载A、abB、abC、2a2b2abD、2ab学习必备欢迎下载点评:易误选A,忽视运用基本不等式“=”成立的条件;学习必备欢迎下载14.数列{an}的通项式ann,就数列{an}中的最大项是(D)n290学习必备欢迎下载A、第9项B、第8项和第9项C、第10项D、第9项和第10项学习必备欢迎下载答案:D点评:易误选A,运用基本不等式,求1an90,忽视定义域N*;n学习必备欢迎下载15.不等式x1x2>a在xnR上有解,就a的取值范畴是(C)学习必备欢迎下载A.3,3B.3,3C.,3D.,3学习必备欢迎下载x22错解:D选D恒成立正解C学习必备欢迎下载16.已知x1,x2是方程x2〔k2〕x〔k23k5〕0〔kR〕的两个实根,就1x2的最大学习必备欢迎下载值为(A)5A、18B、19C、5D、不存在29学习必备欢迎下载x2答案:A错选:B错因:1x2化简后是关于k的二次函数,它的最值依靠于0学习必备欢迎下载所得的k的范畴;17.实数m,n,x,y满意m2+n2=a,x2+y2=a,就mx+ny的最大值是A;学习必备欢迎下载abA、B、abC、2a2b22D、a2b2学习必备欢迎下载答案:B错解:A错因:忽视基本不等式使用的条件,而用\n学习必备欢迎下载学习必备欢迎下载mxnym2x22n2y22ab得出错解;2学习必备欢迎下载11.假如方程(x-1)〔x2-2x+m〕=0的三个根可以作为一个三角形的三条边长,那么实数m的取值范畴是()学习必备欢迎下载A、0≤m≤1B、3<m≤1C、433≤m≤1D、m≥44学习必备欢迎下载2正确答案:(B)错误缘由:不能充分挖掘题中隐含条件;二填空题学习必备欢迎下载1.设a0,bb220,a21,就a1b的最大值为学习必备欢迎下载错解:有消元意识,但没留意到元的范畴;正解:由ab20,b0,2a21得:a21b,22学习必备欢迎下载学习必备欢迎下载且0b21,原式=b2〔1〕〔1b2〕1b43b21,求出最大值为1;学习必备欢迎下载222学习必备欢迎下载2.如x,yR,且xyaxy恒成立,就a的最小值是学习必备欢迎下载学习必备欢迎下载错解:不能敏捷运用平均数的关系,正解:由m2n2mn,得mn2,即学习必备欢迎下载2222mnxy2,故a的最小值是2;xy学习必备欢迎下载3.已知两正数x,y满意x+y=1,就z=〔x1〕〔y1xy〕的最小值为;学习必备欢迎下载学习必备欢迎下载错解一、由于对a>0,恒有a12,从而z=〔x1〕〔y1〕4,所以z的最小值是4;学习必备欢迎下载axy学习必备欢迎下载错解二、z1x2y22xy〔2xy〕222xy22〔21〕,所以z的最小值是学习必备欢迎下载xyxyxy2〔21〕;学习必备欢迎下载错解分析:解一等号成立的条件是11x且yxy,即x1且y1,与xy1相冲突;解二等学习必备欢迎下载学习必备欢迎下载号成立的条件是2xyxy,即xy2,与0xy1相冲突;4\n学习必备欢迎下载学习必备欢迎下载111yx1〔xy〕22xy2学习必备欢迎下载正解:z=〔x〕〔y〕xy=xy=xyxyxyxyxyxyxy1,令t=xy,学习必备欢迎下载学习必备欢迎下载就0txy〔xy〕21,由f〔t〕t21在0,1上单调递减,故当t=时f〔t〕t2学习必备欢迎下载24t44t有最小值33,所以当xy1时z有最小值25;4241.如对于任意x∈R,都有〔m-2〕x2-2〔m-2〕x-4<0恒成立,就实数m的取值范畴是;正确答案:〔-2,2〕;错误缘由:简单忽视m=2;学习必备欢迎下载2.不等式ax2+bx+c>0,解集区间(-1,2),对于系数a、b、c,就有如下结论:2学习必备欢迎下载①a>0②b>0③c>0④a+b+c>0⑤a–b+c>0,其中正确的结论的序号是.正确答案2、3、4错因:一元二次函数的懂得学习必备欢迎下载3.不等式〔x-2〕x2-2x-3≥0的解集是.正确答案:xx1或x3学习必备欢迎下载学习必备欢迎下载4.不等式x2a2x1的解集为(-∞,0),就实数a的取值范畴是;学习必备欢迎下载正确答案:{-1,1}5.如α,β,γ为奇函数f〔x〕的自变量,又f〔x〕是在(-∞,0)上的减函数,且有α+β>0,α+γ>0,β+γ>0,就f〔α〕+f〔β〕与f〔-γ〕的大小关系是:f〔α〕+f〔β〕1,就y=x+2的最小值为x1学习必备欢迎下载学习必备欢迎下载答案:221点评:误填:4,错因:yx2≥22x,当且仅当x2即x=2学习必备欢迎下载x1x1x1时等号成立,忽视了运用基本不等式求最值时的“一正、二定、三相等”的条件;学习必备欢迎下载210.设实数a,b,x,y满意a+b2=1,x22a2x2b2y2a2x2b2y2222+y=3,就ax+by的取值范畴为.学习必备欢迎下载学习必备欢迎下载错解:〔,2〕错因:axby1,当且仅当学习必备欢迎下载学习必备欢迎下载ax,by时等号成立,而此时a2b2x2y2与已知条件冲突;正解:[-3,3]学习必备欢迎下载11..-4<k<o是函数y=kx2-kx-1恒为负值的条件学习必备欢迎下载错解:充要条件错因:忽视k0时y1符合题意;正解:充分非必要条件\n学习必备欢迎下载学习必备欢迎下载x210.函数y=x25的最小值为4学习必备欢迎下载学习必备欢迎下载错解:2错因:可化得yx241x242,而些时等号不能成立;正解:52学习必备欢迎下载11.已知a,bR,且满意a+3b=1,就ab的最大值为.学习必备欢迎下载错解:1错因:由〔a63b〕21,得a26ab9b21,6ab1a29b21,学习必备欢迎下载等号成立的条件是aa0与已知冲突;正解:112学习必备欢迎下载12.设函数yk26xk8的定义域为R,就k的取值范畴是;学习必备欢迎下载错解:9k1错因:对二次函数图象与判别式的关系熟悉不清,误用0;答案:k1学习必备欢迎下载16.不等式〔x-2〕2〔3-x〕〔x-4〕3〔x-1〕0的解集为;学习必备欢迎下载答案:{xx1或x2或3x4}错解:{xx1或3x4}错因:忽视x=2时不等式成立;学习必备欢迎下载x17.已知实数x,y满意yxy,就x的取值范畴是;学习必备欢迎下载学习必备欢迎下载答案:{xx0或x4}错解:{xx0或x4}错因:将方程作变形使用判别式,忽视隐含条学习必备欢迎下载件“y0”;学习必备欢迎下载18.如x,yR,且2x+8y-xy=0就x+y的范畴是;学习必备欢迎下载学习必备欢迎下载答案:[18〕由原方程可得学习必备欢迎下载学习必备欢迎下载y〔x8〕2x,x0,y0,x80,y2x就xyx8161018学习必备欢迎下载x8x8学习必备欢迎下载错解:〔,2][18,〕设xyt设ytx代入原方程使用判别式;学习必备欢迎下载错因:忽视隐含条件,原方程可得y〔x-8〕=2x,就x>8就x+y>8x学习必备欢迎下载19.已知实数x,y满意yxy,就x的取值范畴是;学习必备欢迎下载学习必备欢迎下载正确答案:x0或x4错因:找不到解题思路,另外变形为y2x时易忽视y0这一条件;学习必备欢迎下载20.已知两个正变量x,y满意xy4,就使不等式1xy14ym恒成立的实数m的取值范\n学习必备欢迎下载围是;学习必备欢迎下载正确答案:m9错误缘由:条件x+y=4不知如何使用4学习必备欢迎下载44x213学习必备欢迎下载21已知函数①yxx0②ycosx0x2③y④学习必备欢迎下载xcosxx29学习必备欢迎下载y121cotx14tanx0x2,其中以4为最小值的函数个数是0;学习必备欢迎下载错误缘由:对使用算术平均数和几何平均数的条件意识性不强;学习必备欢迎下载22.已知fx是定义在0,的等调递增函数,fxyfxfy,且f21,就不等式学习必备欢迎下载fxfx32的解集为;学习必备欢迎下载正确答案:x|3x4错误缘由:不能正确转化为不等式组;学习必备欢迎下载23.已知a2+b2+c2=1,x2+y2+z2=9,就ax+by+cz的最大值为+z错误缘由:忽视使用基本不等式时等号成立的条件,易填成5;应使用如下做法:9a2+x2≥6ax,学习必备欢迎下载229b+y2≥6by,9c+z2≥6cz,6〔ax+by+cz〕≤9(a22+b+c2)+9〔x2+y22〕=18,ax+by+cz≤3学习必备欢迎下载三、解答题:xy1.是否存在常数c,使得不等式cxy对任意正数x,y恒成立?学习必备欢迎下载2xyx2yx2y2xy学习必备欢迎下载学习必备欢迎下载错解:证明不等式xyxy恒成立,故说明c存在;学习必备欢迎下载2xyx2yx2y2xy学习必备欢迎下载正解:令x=y得2c22,故猜想c=xy2xy,下证不等式学习必备欢迎下载3332xyx2y3x2y2xy学习必备欢迎下载恒成立;要证不等式xy2,由于x,y是正数,即证3x〔x+2y〕+3y〔2x+y〕≤2xyx2y3学习必备欢迎下载2(2x+y)〔x+2y〕,也即证3x212xy3y22〔2x22y25xy〕,即2xy≤x2y2(恒成立)学习必备欢迎下载学习必备欢迎下载同理不等式2xy也成立,故存在c=2使原不等式恒成立;学习必备欢迎下载3x2y2xy3学习必备欢迎下载1.已知适合不等式x24xpx35的x的最大值为3,求p的值;学习必备欢迎下载错解:对此不等式无法进行等价转化,不懂得“x的最大值为3”的含义;学习必备欢迎下载正解:由于x的最大值为3,故x-3<0,原不等式等价于x24xp〔x3〕5,学习必备欢迎下载即x2x24xpx2,就{x2x25xp3xp20〔1〕,20〔2〕\n学习必备欢迎下载学习必备欢迎下载设(1)(2)的根分别为x1、x2〔x2x1〕,x3、x4〔x4x3〕,就x23或x43学习必备欢迎下载x23,就9-15+p-2=0,p=8x43,就9-9+p+2=0,p=-2当a=-2时,原方程组无解,就p=8如如学习必备欢迎下载21.设f〔x〕axbx,且1f〔1〕2,2f〔1〕4,求f〔2〕的取值范畴;学习必备欢迎下载解:令f〔2〕mf〔1〕nf〔1〕就4a2bm〔ab〕n〔ab〕学习必备欢迎下载4a2b〔mn〕a〔mn〕b比较系数有mn4mn2学习必备欢迎下载m3n1f〔2〕3f〔1〕f〔1〕1f〔1〕2,2f〔1〕53f〔1〕f〔1〕1即5f〔2〕10学习必备欢迎下载说明:此题极易由已知二不等式求出a、b的范畴,然后再求4a2b即f〔2〕的范畴,这学习必备欢迎下载种解法错在已知二不等式中的等号成立的条件不肯定相同,它们表示的区域也不肯定相同,用待定系数法就简单防止上述错误;学习必备欢迎下载1.如mR,解关于x的不等式:〔m23m3〕xm23m3;学习必备欢迎下载学习必备欢迎下载解:令um23m3就uxu学习必备欢迎下载学习必备欢迎下载u〔x1〕0u〔m〕的判别式94〔1〕〔3〕0学习必备欢迎下载u0恒成立x10原不等式的解为x1说明:此题简单由uxu得出x1的错误结论;解有关不等式的问题,肯定要留意含参数的表达式的符号,否就易出错误;3学习必备欢迎下载2.求函数y12x的极大值或微小值;x学习必备欢迎下载学习必备欢迎下载解:当x0时,y12x31〔2xx3〕126x学习必备欢迎下载学习必备欢迎下载当且仅当2x3即x3x2时,y\n学习必备欢迎下载max126\n学习必备欢迎下载当x0时,学习必备欢迎下载y1〔2x〕〔3〕x学习必备欢迎下载12〔2x〕〔3〕x126学习必备欢迎下载学习必备欢迎下载当且仅当2x3即x3x2时,ymin126学习必备欢迎下载说明:此题简单漏掉对x0的争论;不等式ab2ab成立的前提是a0,b0;学习必备欢迎下载1.求函数ysin2xcosx的最大值;学习必备欢迎下载2解:y4sinx2cosx学习必备欢迎下载2221学习必备欢迎下载sinx123sinx2cosx2学习必备欢迎下载〔〕23学习必备欢迎下载2233当且仅当sin2x2cos2x即tgx2时,y23max9学习必备欢迎下载学习必备欢迎下载说明:此题简单这样做:y〔1cos2x)〕cosx〔1cosx〕〔1cosx〕cosx12学习必备欢迎下载学习必备欢迎下载331〔〕;但此时等号应满意条件132cosx1cosxcosx,这样的x是不存在的,错误的学习必备欢迎下载缘由是没有考虑到等号成立的条件;这一点在运用重要不等式时肯定要引起我们高度的重视;学习必备欢迎下载22|x|x1.解不等式:22;学习必备欢迎下载解:当x0时,原不等式为2x2x12xx当x0时,原不等式为2222学习必备欢迎下载x2〔2〕2x又x0x2221021或2x21\n学习必备欢迎下载学习必备欢迎下载2x12x21原不等式的解为x1或x2log2〔21〕学习必备欢迎下载xlog2〔21〕学习必备欢迎下载说明:此题易在x0时2x结果要考虑分段的前提;21处出错,忽视了x0的前提;这提示我们分段求解的9学习必备欢迎下载7.如a0且a1,解不等式:xlogax解:如a1,两边取以a为底的对数x2a2学习必备欢迎下载logxlogx9logx〔2〕学习必备欢迎下载aaa22log2x9logx40aalogx4或logx1aa21xa4或xa2如0a1,同样有,2log2x9logx40aa1logax421a4xa21学习必备欢迎下载又x0当a1时不等式的解为xa4或0xa2学习必备欢迎下载学习必备欢迎下载当0a1时不等式的解为a41xa2学习必备欢迎下载说明:此题易在a1时的解中出错,简单忽视x0这个条件;解决对数问题要留意真数大于0的条件;学习必备欢迎下载8.方程x2〔k2〕x5k0的两根都大于2,求实数k的取值范畴;学习必备欢迎下载学习必备欢迎下载解:设方程的两根为x1,x2,就必有学习必备欢迎下载学习必备欢迎下载〔x1〔x102〕〔x22〕〔x22〕02〕0学习必备欢迎下载学习必备欢迎下载〔k2〕2〔k2〕4〔5k〕040学习必备欢迎下载〔5k〕5k2〔k2〕404\n学习必备欢迎下载说明:此题易犯这样的错误:学习必备欢迎下载x12,x22且xx4和判别式0联立刻得k的范畴学习必备欢迎下载12x1x24学习必备欢迎下载缘由是x12和x22只是x1x24的充分条件学习必备欢迎下载即x1x24不能保证x12和x22同时成立学习必备欢迎下载x27.设函数f〔x〕=logb12x2ax2〔b>0且b≠1〕,学习必备欢迎下载(1)求f〔x〕的定义域;(2)当b>1时,求使f〔x〕>0的全部x的值;解(1)∵x2-2x+2恒正,∴f〔x〕的定义域是1+2ax>0,即当a=0时,f〔x〕定义域是全体实数;1学习必备欢迎下载当a>0时,f〔x〕的定义域是(-,+∞)2a学习必备欢迎下载当a<0时,f〔x〕的定义域是(-∞,-1)2a学习必备欢迎下载(2)当b>1时,在f〔x〕的定义域内,f〔x〕>0x22x12ax2>1x2-2x+2>1+2ax学习必备欢迎下载x2-2〔1+a〕x+1>0其判别式Δ=4〔1+a〕2-4=4a〔a+2〕(i)当Δ<0时,即-20∴f〔x〕>0x<-12a(ii)当Δ=0时,即a=-2或0时学习必备欢迎下载如a=0,f〔x〕>0〔x-1〕2>0x∈R且x≠1学习必备欢迎下载2如a=-2,f〔x〕>0〔x+1〕>0x<〔iii〕当△>0时,即a>0或a<-2时1且x≠-14学习必备欢迎下载学习必备欢迎下载2方程x-2〔1+a〕x+1=0的两根为x1=1+a-a212a,x2=1+a+a22a学习必备欢迎下载如a>0,就x2>x1>0>-2a212学习必备欢迎下载∴f〔x〕0x1aa2a或2ax1aa2a学习必备欢迎下载1如a<-2,就x1x22a\n学习必备欢迎下载学习必备欢迎下载∴f〔x〕>0x<1+a-a22a或1+a+a22a<x<-12a学习必备欢迎下载综上所述:当-2<a<0时,x的取值集合为{x|x<-1}2a当a=0时,x∈R且x≠1,x∈R,当a=-2时:{x|x<-1或-1<x<1}4学习必备欢迎下载当a>0时,x∈{x|x>1+a+a22a或-1<x<1+a-a22a2a}学习必备欢迎下载当a<-2时,x∈{x|x<1+a-a22a或1+a+a22a<x<-1}2a学习必备欢迎下载错误缘由:解题时易忽视函数的定义域,不会合理分类;学习必备欢迎下载10.设集合M=[-1,1],N=[-2222222,2],f〔x〕=2x28+mx-1,如x∈N,m∈M,求证|f〔x〕|≤9学习必备欢迎下载学习必备欢迎下载2证明:|f〔x〕|=|2x+mx-1|=|〔2x-1〕+mx|≤|〔2x-1〕|+|mx|=〔2x-1〕+|mx|≤〔2x-1〕+|x|学习必备欢迎下载1288=-2(|x|-4)+9≤9错因:不知何时使用肯定值不等式;学习必备欢迎下载11.在边长为a的正三角形中,点P、Q、R分别在BC、CA、AB上,且BP+CQ+AR=a设,2三角形PQR的面积为s,求s的最大值及相应的x、y、z的值;解设ΔBPR、ΔPCR、ΔARQ的面积为s1、、s2、s3,就BP=x,CQ=y,AR=z,学习必备欢迎下载S=SΔABC-S1-S2-S3=324a-34[a-(xy+xz+yz)]=34(xy+xz+yz)学习必备欢迎下载2a32a学习必备欢迎下载由x+y+z=a,得xy+yz+zx≤3,∴Smav=12a,此时,x=y=z=3学习必备欢迎下载错因:不知如何使用基本不等式;学习必备欢迎下载12.设a、b∈R,求证:|a1|ab|≤b||a|1|a||b|1|b|学习必备欢迎下载证明:当|a+b|=0时,不等式已成立当|a+b|≠0时,∵|a+b|≤|a|+|b|学习必备欢迎下载|a∴1|ab|=b|11≤11|ab|1|a|1|b||a|=|a||b||b|1学习必备欢迎下载|a|=1|a|+|b|1|b||a|≤|b||a|1|a||b|1|b|学习必备欢迎下载点评:错证:∵|a+b|≤|a|+|b|学习必备欢迎下载|a∴1|ab|≤b||a|1|a||b||b||a|1|a||b||b|1|a|≤|b||a|1|a||b|①1|b|\n学习必备欢迎下载错因:①的推理无依据;