高中数学 寒假专题复习资料 第三讲 概率 新人教a版必修3 10页

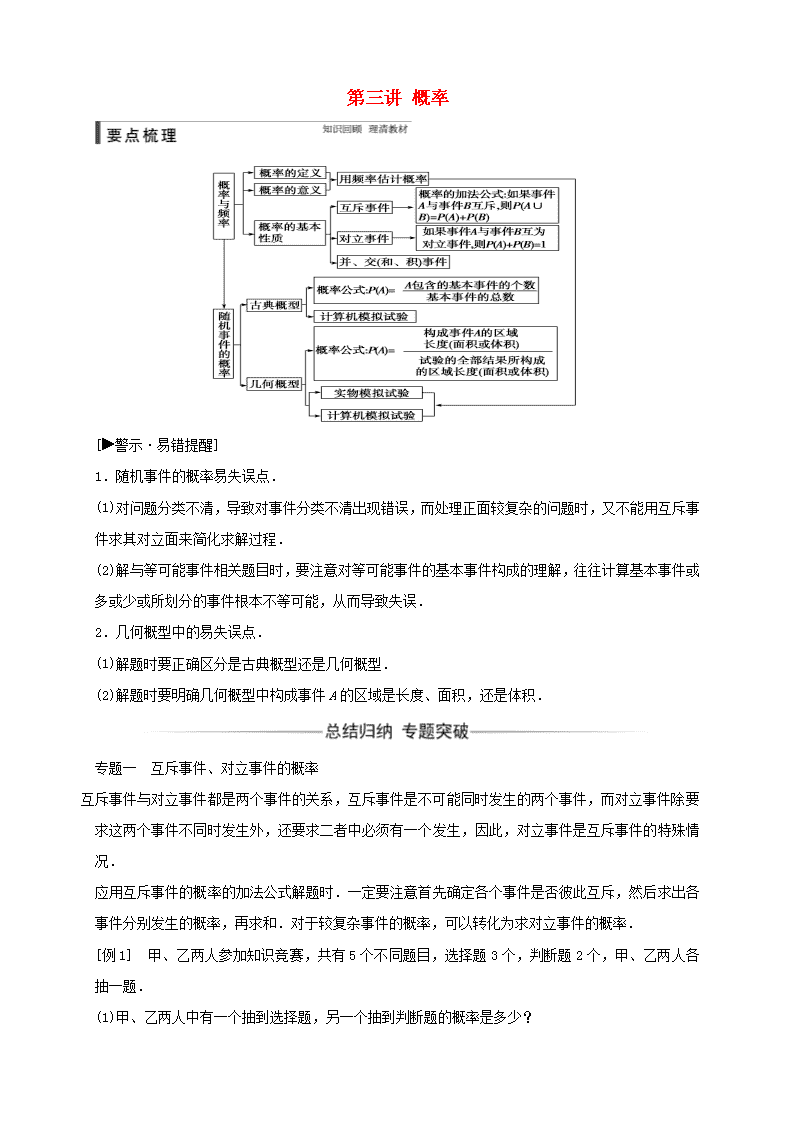
第三讲概率[警示·易错提醒]1．随机事件的概率易失误点．(1)对问题分类不清，导致对事件分类不清出现错误，而处理正面较复杂的问题时，又不能用互斥事件求其对立面来简化求解过程．(2)解与等可能事件相关题目时，要注意对等可能事件的基本事件构成的理解，往往计算基本事件或多或少或所划分的事件根本不等可能，从而导致失误．2．几何概型中的易失误点．(1)解题时要正确区分是古典概型还是几何概型．(2)解题时要明确几何概型中构成事件A的区域是长度、面积，还是体积．专题一　互斥事件、对立事件的概率，，，互斥事件与对立事件都是两个事件的关系，互斥事件是不可能同时发生的两个事件，而对立事件除要求这两个事件不同时发生外，还要求二者中必须有一个发生，因此，对立事件是互斥事件的特殊情况．应用互斥事件的概率的加法公式解题时．一定要注意首先确定各个事件是否彼此互斥，然后求出各事件分别发生的概率，再求和．对于较复杂事件的概率，可以转化为求对立事件的概率．[例1]　甲、乙两人参加知识竞赛，共有5个不同题目，选择题3个，判断题2个，甲、乙两人各抽一题．(1)甲、乙两人中有一个抽到选择题，另一个抽到判断题的概率是多少？\n(2)甲、乙两人中至少有一人抽到选择题的概率是多少？归纳升华1．互斥事件与对立事件的概率计算．(1)若事件A1，A2，…，An彼此互斥，则P(A1∪A2∪…∪An)＝P(A1)＋P(A2)＋…＋P(An)．(2)设事件A的对立事件是，则P(A)＝1－P()．2．求复杂事件的概率常用的两种方法．(1)将所求事件转化成彼此互斥的事件的和．(2)先求其对立事件的概率，然后再应用公式P(A)＝1－P()求解．[变式训练]　2016年5月1日某购物中心举行“庆五一回报顾客”的超低价购物有礼活动，某人对购物中心交款处排队等候付款的人数及其概率统计如下表所示．求：排队人数020304050≥50概率0.10.160.30.30.10.04(1)至多30人排队的概率；(2)至少30人排队的概率．专题二　古典概型古典概型是一种最基本的概型，也是学习其他概型的基础，在高考题中，经常出现此种概型的题目，解题时要紧紧抓住古典概型的两个基本特征，即有限性和等可能性．对于古典概型概率的计算，关键是分清基本事件个数n与事件A中包含的结果数m，有时需用列举法把基本事件一一列举出来，再利用公式P(A)＝求出事件的概率，这是一个形象、直观的好方法，但列举时必须按某一顺序做到不重复、不遗漏．[例2]　(2014·山东卷)海关对从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量(单位：件)如下表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.地区ABC数量50150100(1)求这6件样品中来自A，B，C各地区商品的数量；(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．归纳升华求解古典概型概率问题的关键是找出样本空间中基本事件的总数及所求事件所包含的基本事件数，常用方法是列举法、列表法、画树状图法等．\n[变式训练]　(2015·课标全国Ⅰ卷)如果3个正整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1，2，3，4，5中任取3个不同的数，则这3个数构成一组勾股数的概率为(　　)A.　　　　B.　　　　C.　　　　D.专题三　几何概型几何概型有两大特征：基本事件的无限性和每个事件发生的等可能性．求解此类问题时，常把概率问题等价转化为相应问题的测度比问题．常见的测度比有长度之比、面积之比、体积之比等，正确区分几何概型与古典概型是本章学习的一个难点．[例3]　已知区域E＝{(x，y)|0≤x≤3，0≤y≤2}，F＝{(x，y)|0≤x≤3，0≤y≤2，x≥y}，若向区域E内随机投掷一点，则该点落入区域F内的概率为________．归纳升华对于几何概型的概率公式中的“测度”要有正确的认识，它只与大小有关，而与形状和位置无关，在解题时，要掌握“测度”为长度、面积、体积、角度等常见的几何概型的概率求解方法，主要有下面两种类型：(1)线型几何概型：基本事件受一个连续的变量控制．(2)面积几何概型：基本事件受两个连续的变量控制．一般是把两个变量分别作为一个点的横坐标和纵坐标，这样基本事件就构成了平面上的一个区域，即可借助平面区域解决．[变式训练]　在区间[－3，3]上随机取一个数x，使得不等式|x＋1|－|x－2|≥1成立的概率为________．专题四　概率与统计的综合问题统计和古典概型的综合是高考解答题的一个命题趋势和热点，此类题很好地结合了统计与概率的相关知识，并且在实际生活中应用也十分广泛，能很好地考查学生的综合解题能力，在解决综合问题时，要求同学们对图表进行观察、分析、提炼，挖掘出图表所给予的有用信息，排除有关数据的干扰，进而抓住问题的实质，达到求解的目的．[例4]　(2015·课标全国Ⅱ卷)某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表．满意度评[50，60)[60，70)[70，80)[80，90)[90，100]\n分分组频数2814106(1)作出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值，给出结论即可)．B地区用户满意度评分的频率分布直图(2)根据用户满意度评分，将用户的满意度分为三个等级，如下表所示．满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大，并说明理由．归纳升华　本题通过画频率分布直方图考查对数据的处理能力和数形结合的思想方法，通过求概率考查运算求解能力和实际应用意识．[变式训练]　随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如图所示．(1)直接根据茎叶图判断哪个班的平均身高较高；(2)计算甲班的样本方差；(3)现从乙班这10名同学中随机抽取2名身高不低于173cm的\n专题五　转化与化归思想本章中多次用到了转化与化归思想，比如在求解概率时，有时要转化为求互斥事件的和事件，有时要转化为求对立事件，有时还要将代数问题转化为几何问题等．[例5]　在|p|≤3，|q|≤3的前提下，随机取数对(p，q)，试求方程x2＋2px－q2＋1＝0有两个实数根的概率．归纳升华这里把一个方程根的问题转化为平面区域上的图形面积问题，从而使问题得到了解决，这里的转化起到了“化抽象为具体”的作用．[变式训练]　一个箱子内有9张票，其号码分别为1，2，…，8，9.从中任取2张，其号码至少有一个为奇数的概率是多少？\n\n\n\n\n