初中数学分类讨论方法篇课件 18页

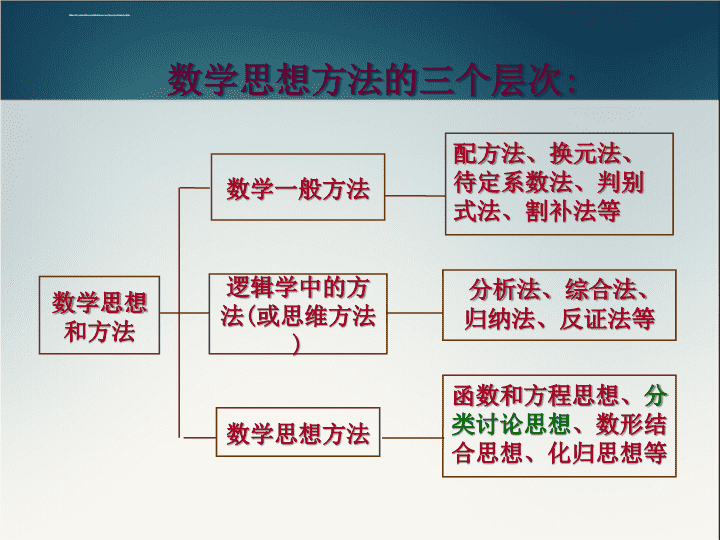
初中数学学习方法篇分类讨论讲师：李#\n数学思想方法的三个层次:数学思想和方法数学一般方法逻辑学中的方法(或思维方法)数学思想方法配方法、换元法、待定系数法、判别式法、割补法等分析法、综合法、归纳法、反证法等函数和方程思想、分类讨论思想、数形结合思想、化归思想等\n分类讨论思想（方法）介绍在解答某些数学问题时，因为存在一些不确定的因素，解答无法用统一的方法或结论不能给出统一的表述，对这类问题依情况加以分类，并逐类求解，然后综合求解，这种解题的方法叫分类讨论法.分类讨论涉及初中数学的所有知识点，其关键是弄清引起分类的原因，明确分类讨论的对象和标准，分情况加以讨论求解，再将不同结论综合归纳，得出正确答案。注意分类的原则是既不重复，也不遗漏！\n一张矩形纸片有四个角，剪掉一个角后，还剩几个角？分类讨论是一种重要的数学思想，当研究对象的元素或其关系不明确时，常需要对研究对象元素或各元素之间关系的各种可能进行分类讨论。思考引入\n1、如图，线段OD的一个端点O在直线OM上，∠DOM=30°,以OD为一边画等腰三角形，并且使另一个顶点P在直线OM上，这样的等腰三角形能画多少个?ＯＤ30°⌒P1MP3P4P2分类：⑴以OD为底边⑵以OD为腰首先要找到合适的分类标准！P是OD的中垂线与OM的交点。P是分别以O,D为圆心,OD为半径的圆与直线OM的交点。探索发现\nＯＤ30°⌒P1MP3P4P2思考：当∠DOM=60°,符合条件的点P有几个，当∠DOM=90°呢?ＤＯ60°⌒MP2P1ＯＤ90°MP2P1\n2、在下图三角形的边上找出一点，使得该点与三角形的两顶点构成等腰三角形！ACB50°110°20°探索发现\n1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论CABACB20°20°20°20°CAB50°50°CAB80°80°20°CAB65°65°50°CAB35°35°110°（分类讨论）ACB50°110°20°\n探索发现\n4、已知一次函数y=kx+b，当－３≤ｘ≤１时，对应ｙ的值为１≤ｙ≤９.则ｋ·ｂ的值（）（Ａ）１４　　　（Ｂ）－６（Ｃ）－６或２１　　（Ｄ）－６或１４探索发现\n1、A为数轴上表示-1的点，将点A沿数轴平移3个单位到B，则点B所表示的实数为（）A、2B、2C、-4D、2或-42、在平面直角坐标系中，三点坐标分别是（0，0）（4，0）（3，2），以三点为顶点画平行四边形，则第四个顶点不可能在（）A、第一象限B、第二象限C、第三象限D、第四象限DC链接中考\n(3,2)(4,0)(0,0)(7,2)(-1,2)(1,-2)\n3、如图，在△ABC中，AB=12，AC=15，点D在AB上，且AD=8，在AC上取一点E,使得以A、D、E为顶点的三角形与△ABC相似，求AE的长.(1)EABCD(2)EABCD△ADE∽△ABC或△ADE∽△ACB\n解：①如图（1），过D作DE∥BC交AC于E，则∠ADE=∠B,∠AED=∠C,∴△ADE∽△ABC.∴,又∵AB=12，AC=15，AD=8，∴AE=10.②如图（2），作∠ADE=∠C交AC于E，又∵∠A=∠A,∴△ADE∽△ACB.∴,又∵AB=12，AC=15，AD=8，∴AE=6.4.由①、②得：AE长为10或6.4.\nｙＤＯＣＢＡＸ已知二次函数ｙ＝２ｘ２－２的图像与ｘ轴交于Ａ、Ｂ两点（点Ａ在点Ｂ的左边），与ｙ轴交于点Ｃ,直线ｘ＝ｍ（ｍ＞１）与ｘ轴交于点Ｄ。（１）求Ａ、Ｂ、Ｃ三点的坐标；（２）在直线ｘ＝ｍ（ｍ＞１）上有一点Ｐ（点Ｐ在第一象限），使得以Ｐ、Ｄ、Ｂ为顶点的三角形与以Ｂ、Ｃ、Ｏ为顶点的三角形相似，求点Ｐ的坐标。课后思考\n解（1）A（－1，0），B（1，0），C（０，－2）当△PDB∽△COB时，有P（m,2m－2）；(2)当△PDB∽△BOC时，=有Ｐ（ｍ，　－　）ＤＯＣＢＡＸP\n1、先明确需讨论的对象；2、选择分类的标准，合理分类；（统一标准，不重不漏）3、逐类讨论；4、归纳作出结论。分类讨论思想解决问题的一般步骤：统一标准，不重不漏课后小结\n同学们，再见！讲师：李#