【资料】高中数学必修一第一章集合与函数的概念复习资料 35页

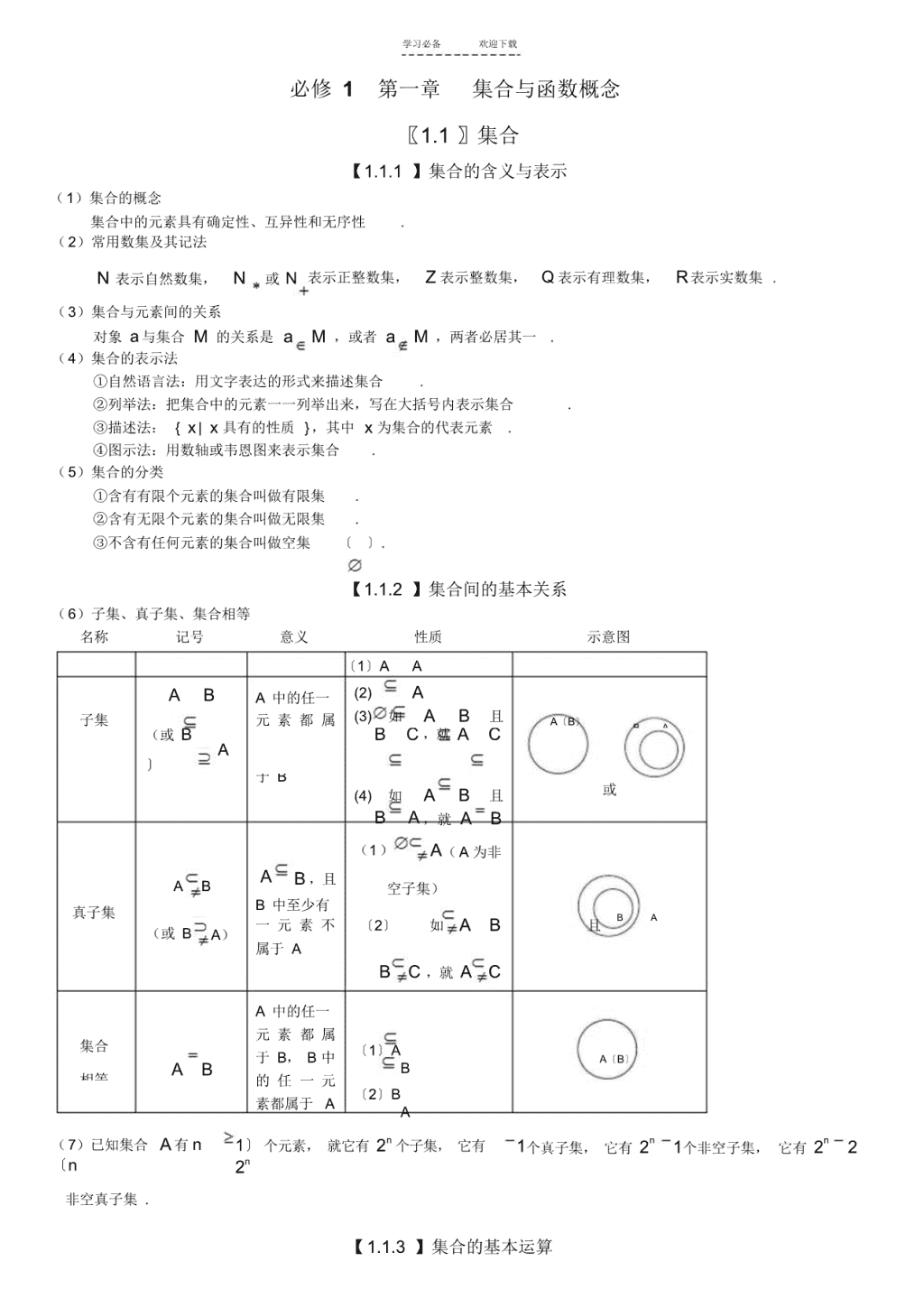
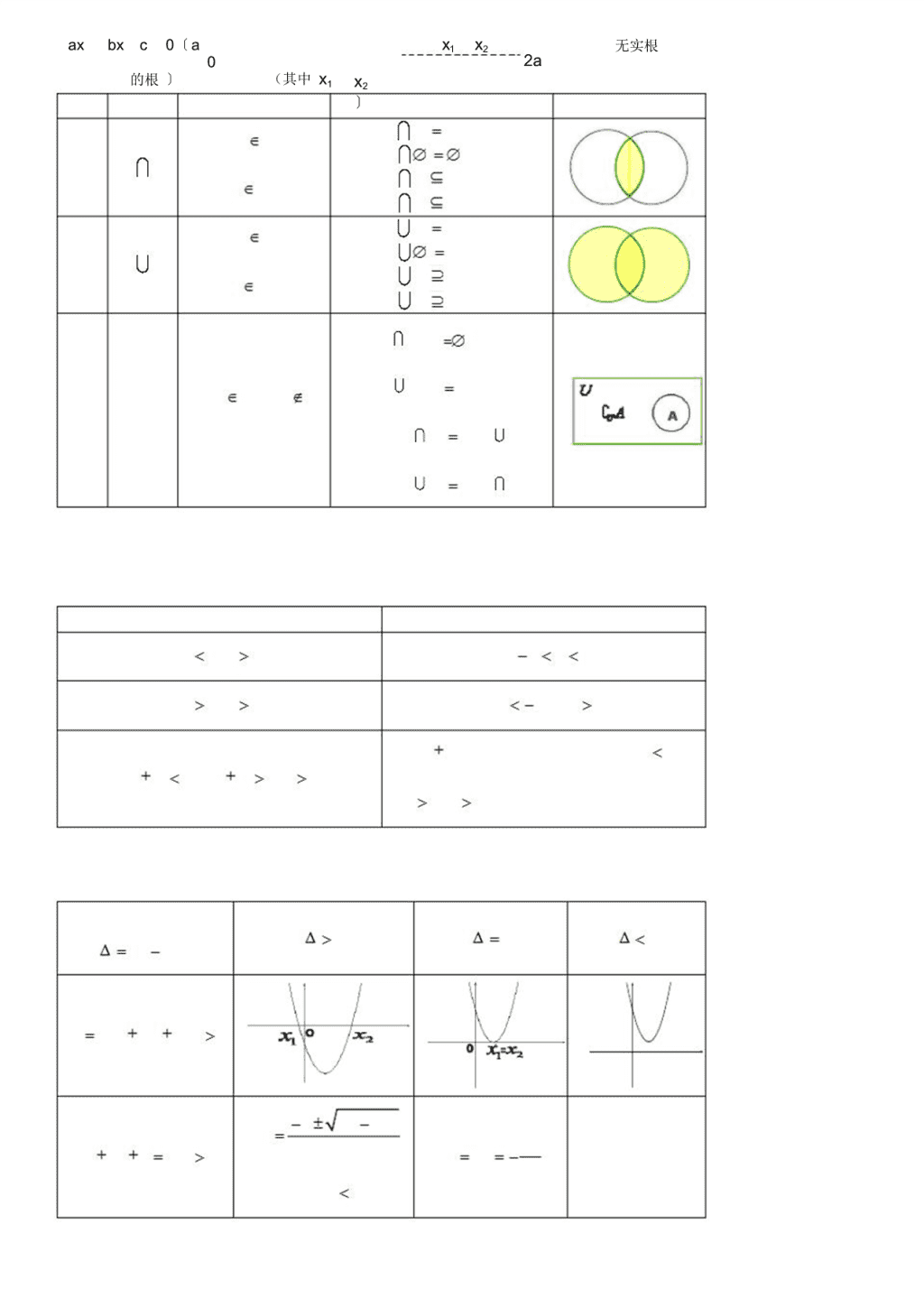
学习必备欢迎下载必修1第一章集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性.（2）常用数集及其记法N表示自然数集，N或N表示正整数集，Z表示整数集，Q表示有理数集，R表示实数集.（3）集合与元素间的关系对象a与集合M的关系是aM，或者aM，两者必居其一.（4）集合的表示法①自然语言法：用文字表达的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合.③描述法：{x|x具有的性质}，其中x为集合的代表元素.④图示法：用数轴或韦恩图来表示集合.（5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集〔〕.【1.1.2】集合间的基本关系（6）子集、真子集、集合相等名称记号意义性质示意图〔1〕AAABA中的任一(2)A子集元素都属(3)如AB且A〔B〕BA（或BBC，就ACA〕于B或(4)如AB且BA，就AB（1）A（A为非AB，且AB空子集）B中至少有真子集BA一元素不〔2〕如AB且（或BA）属于ABC，就ACA中的任一元素都属集合〔1〕A于B，B中A〔B〕ABB相等的任一元〔2〕B素都属于AAnnn（7）已知集合A有n1〕个元素，就它有2个子集，它有1个真子集，它有21个非空子集，它有22〔nn2非空真子集.【1.1.3】集合的基本运算\n学习必备欢迎下载（8）交集、并集、补集名称记号意义性质示意图（1）AAA{x|xA,且（2）A交集AB（3）ABABAxB}ABB（1）AAA{x|xA,或（2）AA并集AB（3）ABAABxB}ABB（1）A〔eUA〕（2）A〔eUA〕U{x|xU,且xA}补集eUA（3）痧U〔B〔A〔.UA〕U〕B〕（4）痧U〔B〔A〔.UA〕U〕B〕【补充学问】含肯定值的不等式与一元二次不等式的解法（1）含肯定值的不等式的解法不等式解集|x|a〔a{x|axa}0〕|x|a〔ax|xa或xa}0〕把axb看成一个整体，化成|x|a，|axb|c,|axb|c〔c0〕|x|a0〕型不等式来求解〔a（2）一元二次不等式的解法判别式2000b4ac二次函数2yaxbxc〔a0〕O的图象一元二次方程2bb4ac2x1,22ab\naxbxc0〔ax1x2无实根02a的根〕（其中x1x2〕\n学习必备欢迎下载2axbxc0〔ab{x|xx1或xx2}{x|x}R02a的解集〕2axbxc0〔a0〕{x|x1xx2}的解集〖1.2〗函数及其表示【1.2.1】函数的概念（1）函数的概念①设A、B是两个非空的数集，假如依据某种对应法就f，对于集合A中任何一个数x，在集合B中都有唯独确定的数f〔x〕和它对应，那么这样的对应（包括集合A，B以及A到B的对应法就f）叫做集合A到B的一个函数，记作f:AB．②函数的三要素:定义域、值域和对应法就．③只有定义域相同，且对应法就也相同的两个函数才是同一函数．（2）区间的概念及表示法①设a,b是两个实数，且ab，满意axb的实数x的集合叫做闭区间，记做[a,b]；满意axb的实数x的集合叫做开区间，记做〔a,b〕；满意axb，或axb的实数x的集合叫做半开半闭区间，分别记做，〔a,；满足xa,xa,xb,xb的实数x的集合分别记做[a,b〕b][a,〕,〔a,〕,〔,b],〔,b〕．留意：对于集合{x|axb}与区间〔a,b〕，前者a可以大于或等于b，而后者必需ab．（3）求函数的定义域时，一般遵循以下原就：①f是整式时，定义域是全体实数．〔x〕②f是分式函数时，定义域是使分母不为零的一切实数．〔x〕③f是偶次根式时，定义域是使被开方式为非负值时的实数的集合．〔x〕④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1．⑤ytanx中，xk〔kZ〕．2⑥零（负）指数幂的底数不能为零．\n⑦如f〔x〕是由有限个基本初等函数的四就运算而合成的函数时，就其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：如已知f〔x〕的定义域为，其复合函数f[g〔x〕]的定[a,b]义域\n学习必备欢迎下载应由不等式agb解出．〔x〕⑨对于含字母参数的函数，求其定义域，依据问题详细情形需对字母参数进行分类争论．⑩由实际问题确定的函数，其定义域除使函数有意义外，仍要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，假如在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法：①观看法：对于比较简洁的函数，我们可以通过观看直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后依据变量的取值范畴确定函数的值域或最值．③判别式法：如函数yf〔x〕可以化成一个系数含有y的关于x的二次方程ab〔y〕xc〔y〕〔y〕0，就2x2在a〔y〕0时，x,y为实数，故必需有b〔y〕c〔y〕0，从而确定函数的值域或最值．由于4a〔y〕④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题．⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值．⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值．⑧函数的单调性法．【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系．（6）映射的概念①设A、B是两个集合，假如依据某种对应法就f，对于集合A中任何一个元素，在集合B中都有唯独的元素和它对应，那么这样的对应（包括集合A，B以及A到B的对应法就f）叫做集合A到B的映射，记作f:AB．②给定一个集合A到集合B的映射，且aA,bB．假如元素a和元素b对应，那么我们把元素b叫做元素a的象，元素a叫做元素b的原象．〖1.3〗函数的基本性质【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法函数的定义图象判定方法性质\n学习必备欢迎下载假如对于属于定义域I内（1）利用定义某个区间上的任意两个yy=f（2）利用已知函数自变量的值x1、x2,当x．1<．〔X〕f的单调性．x2时，都有f〔x1〕f〔x（3）利用函数图象2〕，．．．．．．．．．．f〔x2〕（在某个区间图那么就说f〔x〕在这ox1x2x象下降为减）个区间上是减函数．．．．（4）利用复合函数②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数yf[gugyf〔u〕为ug〔x〕为yf[g〔x〕]为增；〔x〕]，令〔x〕，如增，增，就如yf〔u〕为ug〔x〕为yf[g〔x〕]为yf〔u〕为增，ug〔x〕为yf[g〔x〕]减，减，就增；如减，就为减；如yf〔u〕为减，ug〔x〕为yf[g〔x〕]为增，就减．ya（2）打“√”函数fx0〕的图象与性质〔x〔ax〕f分别在〔,a]、[a,〕上为增函数，分〔x〕别在[a,0、a]上为减函数．〕〔0,（3）最大（小）值定义ox①一般地，设函数yf〔x〕的定义域为I，假如存在实数M满意：（1）对于任意的xI，都有f〔x〕M；（2）存在x0I，使得fM．那么，我们称M是〔x0〕函数f〔x〕的最大值，fmax〔x〕M．记作②一般地，设函数yf〔x〕的定义域为I，假如存在实数m满意：f〔x〕（1）对于任意的xI，都有m；（2）存在x〕m那么，我们称f〔xm〕是函数0I，使得f〔x0．\n的最小值，记作fmax〔x〕m．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法函数的定义图象判定方法性质\n学习必备欢迎下载假如对于函数f〔x〕（1）利用定义（要先判肯定义定义域内域是否关于原点对称）任意一个x，都有（2）利用图象（图象关于原点对f．〔．－．x．．〕．=－．f．〔．x〕．,那么称）函数函数的f〔x〕叫做奇．函．数．．（1）利用定义（要先判肯定义奇偶性域是否关于原点对称）假如对于函数f〔x〕（2）利用图象（图象关于y轴定义域内对称）任意一个x，都有f．〔．－．x．．〕．=f．〔．x〕．,那么函数f〔x〕叫做偶．函．数．．②如函数f为奇函数，且在x0处有定义，就f〔0〕0．〔x〕③奇函数在y轴两侧相对称的区间增减性相同，偶函数在y轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充学问〗函数的图象（1）作图利用描点法作图：①确定函数的定义域；②化解函数解析式；③争论函数的性质（奇偶性、单调性）；④画出函数的图象．利用基本函数图象的变换作图：要精确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象．①平移变换h0,左移h个单位k0,上移k个单位yfh0,右移|h|个单位yf〔xyfk0,下移|k|个单位yf〔x〕k〔x〕h〕〔x〕01,伸0A1,缩②伸缩变换yf1,缩yf〔yfA1,伸yAf〔x〕〔x〕x〕〔x〕xy轴③对称变换yf〔x〕yfyf〔x〕yf〔x〕轴〔x〕原点直线yx1yf〔x〕yf〔yfyf〔x〕x〕〔x〕去掉y轴左边图象yf保留y轴右边图象，并作其关于y轴对称图象yf〔|x|〕〔x〕保留x轴上方图象yf〔将x轴下方图象翻折上去y|f〔x〕|x（2）识图〕对于给定函数的图象，要能从图象的左右、上下分别范畴、变化趋势、对称性等方面争论函数的定义域、值域、单调性、奇偶性，留意图象与函数解析式中参数的关系．（3）用图：函数图象形象地显示了函数的性质，为争论数量关系问题供应了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．\n第一章集合与函数概念第一讲集合\n学习必备欢迎下载★热点考点题型探析考点一：集合的定义及其关系题型1：集合元素的基本特点[例1]（20XX年江西理）定义集合运算：ABz|zxy,xA,yB．设A1,2,B0,2，就集合AB的全部元素之和为（）A．0；B．2；C．3；D．6[解题思路]依据AB的定义，让x在A中逐一取值，让y在B中逐一取值，xy在值就是AB的元素[解析]：正确解答此题,必需清晰集合AB中的元素，明显，依据题中定义的集合运算知AB=0,2,4，故应挑选D【名师指引】这类将新定义的运算引入集合的问题由于背景公正，所以成为高考的一个热点，这时要充分懂得所定义的运算即可，但要特殊留意集合元素的互异性；题型2：集合间的基本关系[例2]．数集X〔1〕,nZ与Y〔1〕,kZ之的关系是（）2n4kA．XY；B．YX；C．XY；D．XY[解题思路]可有两种思路：一是将X和Y的元素列举出来，然后进行判定；也可依挑选支之间的关系进行判定；[解析]从题意看，数集X与Y之间必定有关系，假如A成立，就D就成立，这不行能；同样，B也不能成立；而假如D成立，就A、B中必有一个成立，这也不行能，所以只能是C【名师指引】新定义问题是高考的一个热点，解决这类问题的方法就是严格依据题中的定义，逐个进行检验，不便利进行检验的，就设法举反例；考点二：集合的基本运算222[例3]设集合Axx3x20，Bxx21〔a5〕0〔〕ax（1）如AB2，求实数a的值；（2）如ABA，求实数a的取值范畴如AB2，[解题思路]对于含参数的集合的运算，第一解出不含参数的集合，然后依据已知条件求参数；2[解析]由于Axx3x201,2，22（1）由AB2知，2B，从而得24〔a〔a0，即15〕〕2a4a30，解得a1或a32当a1时，Bxx402,2，满意条件；2当a3时，Bxx4x402，满意条件所以a1或a3（2）对于集合B，由4145〕8〔a3〕〔〕〔a22a\n由于ABA，所以BA\n学习必备欢迎下载①当0，即a3时，B，满意条件；②当0，即a3时，B2，满意条件；③当0，即a3时，BA1,2才能满意条件，5122〔aa由根与系数的关系得12，冲突12a2〕a725故实数a的取值范畴是a3【名师指引】对于比较抽象的集合，在探究它们的关系时，要先对它们进行化简；同时，要留意集合的子集要考虑空与不空,不要忘了集合本身和空集这两种特殊情形.第2讲函数与映射的概念求值域的几种常用方法2（1）配方法：对于（可化为）“二次函数型”的函数常用配方法，如求函数ysinx2cosx4，可变为2ysinx2cosx4〔cos12解决x〕2（2）基本函数法：一些由基本函数复合而成的函数可以利用基本函数的值域来求，如函数22ylog1〔x2x3〕就是利用函数ylog1u和ux2x3的值域来求；22（3）判别式法：通过对二次方程的实根的判别求值域；如求函数2x1的值域y2x2x221由y2x1得yx21〕2y10，如y0，就得x，所以y0是函数值域中的一个2x2x2〔x2y313值；如y0，就由[21〕]4y〔2y0得313y且y0，故所求值域是〔y2122〕313313[,]222cosx3（4）分别常数法：常用来求“分式型”函数的值域；如求函数y的值域，由于cosx152cosx35，而cosx1〔0,2]，所5,]，故y2cosx1cosx1以21〔cosx1y〔,]23x（5）利用基本不等式求值域：如求函数y的值域2x4344当x0时，y0；当x0时，y，如x0，就x2x44xxx\nx4433如x0，就x〔x2〔4，从而得所求值域是[,]x〕〔44xx〕4〕x\n学习必备欢迎下载42（6）利用函数的单调性求求值域：如求函数y2xx2[的值域〔x1,2]〕11342因y8x2x2x〔41〕，故函数y2xx2[1,2]〕在〕上递减、在,0〕上递增、22x〔x〔1,〔21115在〔0,〕上递〔,上递增，从而可得所求值域为[,30]8减、在2〕22（7）图象法：假如函数的图象比较简洁作出，就可依据图象直观地得出函数的值域（求某些分段函数的值域常用此法）；★热点考点题型探析考点一：判定两函数是否为同一个函数[例1]试判定以下各组函数是否表示同一函数？233（1）fx，gx；〔x〔x〕〕x1x0,（2）f，g〔x〔x〕1x0;x〕2n12n111*（3）fx，g〔x〕（n∈N）；2n2n〔x〔x〕〕2（4）fxx1，gxx；〔x〔x〕〕2（5）fx2x1，g〔t〕2t1〔x2t〕[解题思路]要判定两个函数是否表示同一个函数，就要考查函数的三要素；233[解析]（1）由于fxx，gxx，故它们的值域及对应法就都不相同，所以它们不是同一〔x〔x〕函数.〕x1x0,（2）由于函数f的定义域为,0〔〕，g的定义域为R，所以它们〔x〕0,而〔x1x0;〔不是同一函数.〕x〕*2n12n11（3）由于当n∈N时，2n±1为奇数，∴fxx，g〔x〕x，它们的定义域、2n2n1〔x〔x〕〕值域及对应法就都相同，所以它们是同一函数.（4）由于函数f〕xx0，而g〔x〕1的定义域为xx〔x\n2域为xxxx的定义0或x1，它们的定义域不同，所以它们不是同一函数.（5）函数的定义域、值域和对应法就都相同，所以它们是同一函数.[答案]（1）、（2）、（4）不是；（3）、（5）是同一函数【名师指引】构成函数的三个要素是定义域、对应关系和值域．由于值域是由定义域和对应关系确定的，所以，假如两个函数的定义域和对应关系完全一样，即称这两个函数为同一函数；第（5）小题易错判定成它们是不同的函数；缘由是对函数的概念懂得不透，在函数的定义域及对应法就f不变的条件下，自变量变换字母对于函数本身并22无影响，比如fx1，ft1，f〔u〔u1都可视为同一函数.〔x〔t112〕〕〕〕考点二：求函数的定义域、值域题型1：求有解析式的函数的定义域122[例2].（08年湖北）函数fln〔x3x2x3x4〕的定义域为〔〕〔xx〕\n学习必备欢迎下载A.,[2,〕;B.4,0〔0,1〕；C.4,0〔0,1];[,〔0,1〕〔4〔〕[,〕D.4,0〕〕[解题思路]函数的定义域应是使得函数表达式的各个部分都有意义的自变量的取值范畴；[解析]欲使函数f有意义，必需并且只需〔x〕2x3x202x3x40x[〔0,1〕，故应挑选D22x3x2x3x404,0〕x0【名师指引】如没有标明定义域，就认为定义域为使得函数解析式有意义的x的取值范畴，实际操作时要留意：①分母不能为0；②对数的真数必需为正；③偶次根式中被开方数应为非负数；④零指数幂中，底数不等于0；⑤负分数指数幂中，底数应大于0；⑥如解析式由几个部分组成，就定义域为各个部分相应集合的交集；⑦假如涉及实际问题，仍应使得实际问题有意义，而且留意：争论函数的有关问题肯定要留意定义域优先原就，实际问题的定义域不要漏写；题型2：求抽象函数的定义域2xx2[例3]（2006·湖北）设fxlg，就ff的定义域为（）2x2xA.4,00,4；B.4,11,4；C.2,11,2；D.4,22,4[解题思路]要求复合函数fx2的定义域，应先求f〔的定义域；f2xx〕22,x2x2[解析]由0得，f的定义域为2x2，故2x〔x222.〕xx2解得x4,11,4；故ff的定义域为4,11,4.选B.2x【名师指引】求复合函数定义域,即已知函数f的定义为[a,b]，就函数f[g〔x〕]的定义域是满意不等式〔x〕agb的x的取值范畴；一般地，如函数f[g〔x〕]的定义域是[a,b]，指的[a,b]，要求f〔x〕的〔x〕是x定义域就是x[a,b]时g〔x〕的值域；题型3；求函数的值域2[例4]已知函数yx4ax2a6R〕，如0恒成立，求f2aa3的值域〔ay〔a〕[解题思路]应先由已知条件确定a取值范畴，然后再将f中的肯定值化去之后求值域2〔a3〕\n[解析]依题意，y0恒成立，就16a4〔2a0，解得1a，62〕1719所以f〔2a〔a〔a，从而fmaxf〔4，f〔minf〔，所以fa3〕34〔a1a34〔a〕2〕〕〕〕〕〕2219的值域是[,4]4【名师指引】求函数的值域也是高考热点，往往都要依据函数的单调性求函数的最值；考点三：映射的概念[例5]（06陕西）为确保信息安全，信息需加密传输，发送方由明文密文（加密），接收方由密文明文（解\n学习必备欢迎下载密），已知加密规章为：明文a,b,c,d对应密文a2b,2bc,2c3d,4d.例如，明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时，就解密得到的明文为（）A．7,6,1,4；B．6,4,1,7；C．4,6,1,7；D．1,6,4,7[解题思路]密文与明文之间是有对应规章的，只要依据对应规章进行对应即可；[解析]当接收方收到密文14，9，23，28时，a2b14a62bc9b4有，解得，解密得到的明文为C．2c3d23c14d28d7【名师指引】懂得映射的概念，应留意以下几点：（1）集合A、B及对应法就f是确定的，是一个整体系统；（2）对应法就有“方向性”，即强调从集合A到集合B的对应，它与从集合B到集合A的对应关系一般是不同的；61（3）集合A中每一个元素，在2集合B中都有象，并且象是5唯独．．的，这是映射区分于一般对应的本质特点；（4）集合A中不同元素，在集合B中对应的象可以是同一个；（5）不要求集合B中的每一个元素在集合A中都有原象.01时间01时间0346时间第3讲函数的表示方法★热点考点题型探析考点1：用图像法表示函数[例1]（09年广东南海中学）一水池有2个进水口,1个出水口,一个口的进、出水的速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示．给出以下3个论断：进水量出水量蓄水量甲乙丙（1）0点到3点只进水不出水；（2）3点到4点不进水只出水；（3）4点到6点不进水不出水．就肯定不正确的论断是〔把你认为是符合题意的论断序号都填上〕.．．．[解题思路]依据题意和所给出的图象，对三个论断进行确认即可；[解析]由图甲知，每个进水口进水速度为每小时1个单位，两个进水口1个小时共进水2个单位，3个小时共进水6个单位，由图丙知①正确；而由图丙知，3点到4点应当是有一个进水口进水，出水口出水，故②错误；由图丙知，4点到6点可能是不进水不出水，也可能是两个进水口都进水，同时出水口也出水，故③不肯定正确；从而肯定不正确的论断是（2）．．．【名师指引】象这类给出函数图象让考生从图象猎取信息的问题是目前高考的一个热点，它要求考生熟识基本的\n学习必备欢迎下载函数图象特点，善于从图象中发觉其性质；高考中的热点题型是“知式选图”和“知图选式”；考点2：用列表法表示函数[例2]（07年北京）已知函数fg分别由下表给出〔x〕〔x，〕x123x123f〔x〕131g321〔x〕就f[g〔1〕]的；满意f[gx的值是值为〔x〕]g[f〔x〕]的[解题思路]这是用列表的方法给出函数，就依照表中的对应关系解决问题；[解析]由表中对应值知f[g〔1〕]〔3〕1；=f当x1时，f[g〔1〕]1,〔g〔1〕3，不满意条件g[f1〕]当x2时，f[gf〔2〕fg〔3〕1，满意条件，〔2〕]3,g[〔2〕]当x3时，f[gf〔1〕〔g〔1〕3，不满意条件，〔3〕]1,g[f3〕]∴满意f[gg[f〔x〕]的x的值是x2〔x〕]【名师指引】用列表法表示函数具有明显的对应关系，解决问题的关键是从表格发觉对应关系，用好对应关系即可；考点3：用解析法表示函数题型1：由复合函数的解析式求原先函数的解析式21x1x[例3]（04湖北改编）已知f〕=，就f的解析式可取为2〔〔x〕1x1x[解题思路]这是复合函数的解析式求原先函数的解析式，应当首选换元法1xt12t2x[解析]令t，就x，∴f〔.∴f〔x〕2.1xt1tt1x12〕2x故应填21x\n【名师指引】求函数解析式的常用方法有：①换元法（留意新元的取值范畴）；②待定系数法（已知函数类型如：一次、二次函数、反比例函数等）；③整体代换（配凑法）；④构造方程组（如自变量互为倒数、已知f〔x〕为奇函数且g为偶函数等）；〔x〕题型2：求二次函数的解析式[例4]（普宁市城东中学09届高三其次次月考）二次函数f〔x〕f〔xf2x，且f〔0〕1；满意1〔x〕〕⑴求f〔x〕的解析式；\n学习必备欢迎下载⑵在区间[1,1]上，yf〔x〕的图象y2xm的图象上方，试确定实数m的范畴；恒在[解题思路]（1）由于已知f是二次函数，故可应用待定系数法求解；（2）用数表示形，可得求2xmf〔x〔x〕〕对于x[1,1]恒成立，从而通过分别参数，求函数的最值即可；22[解析]⑴设f2f〔x1〕f〔x〕[a1)b〔x1〕c]〔axbxc〕axbxc0)，就〔x〔x〔a〕2axab2a2,a1,与已知条件比较得：解之得，又fc1，ab0b1〔0〕2fxx1〔x〕22⑵由题意得：xx12xm即mx3x1对x1,1恒成立，易得m〔3x1〕min12x【名师指引】假如已知函数的类型，就可利用待定系数法求解；通过分别参数求函数的最值来获得参数的取值范畴是一种常用方法；考点4：分段函数题型1：依据分段函数的图象写解析式[例5]〔07年湖北〕为了预防流感，某学校对教室用药物消毒法进行消毒；已知药物释放过程中，室内每立方米空气中含药量y（毫克）与时间t（小时）成正比；药物释放完毕后，y与t的函数关系式为1a1y（a为常数），如下列图，依据图中供应的信息，回答以下问16题：（Ⅰ）从药物释放开妈，每立方米空气中的含药量y（毫克）与时间t（小时）之间的函数关系式为；（Ⅱ）据测定，当空气中每立方米的含药量降低到0.25毫克以下时，同学方可进教室，那么从药物释放开头，至少需要经过小时后，同学才能回到教室；[思路点拨]依据题意，药物释放过程的含药量y（毫克）与时间t是一次函数，药物释放完毕后，y与t的函数关系是已知的，由特殊点的坐标确定其中的参数，然后再由所得的表达式解决（Ⅱ）[解析]（Ⅰ）观看图象，当0t0.1时是直线，故y10t；当t0.1时，图象过〔0.1,1〕0.1a10t,0t0.11所以1，即a0.1，所以y116160.1,t〔t〕\n0.10.1a0.1a0.5111（Ⅰ）0.25t0.6，所以至少需要经过0.6小时161616【名师指引】分段函数的每一段一般都是由基本初等函数组成的，解决方法是分段处理；题型2：由分段函数的解析式画出它的图象2例6]上·海〕设函fx4x5，在区间[2,6]上画出函数f〔x〕的图像；〔2006数〔x〕\n学习必备欢迎下载[思路点拨]需将来肯定值符号打开，即先解2x4x50，然后依分界点将函数分段表示，再画出图象；22x4x52x1或5x6[解析]fx4x5,如右上图.〔x〔4x1x525〕x〕【名师指引】分段函数的解决方法是分段处理，要留意分段函数的表示方法，它是用联立符号将函数在定义域的各个部分的表达式依次表示出来，同时附上自变量的各取值范畴；第4讲函数的单调性与最值★热点考点题型探析考点1函数的单调性题型1：争论函数的单调性1,x1,[例1]〔2021广东〕设R,函数f1xFfkx,xR.k〔x〔x〔xx1,x〕〕〕1试争论函数F〔x〕的单调性.[解题思路]分段函数要分段处理，由于每一段都是基本初等函数的复合函数，所以应当用导数来争论；11,x1,kx[解析]:由于f1x,所以Ff〔x〕1x,xR.〔xx1,x1〔xkxx1kx〕〕1〔1〕当x<1时，1-〔k,〔x1〕x>0，F〔1xx〕2〕①当k0时，F0在,1〕上恒成立，故F〔x〕在区,1〕上单调递增；〔x〔间〔〕1k②当k0时，令Fk0,1)，解得x1，2〔x〔1x〕〔xk〕kk且当x1时，F〔0；当1x1时，F〔x〕0kxk〕kk故F〔x〕在区间〕上单调递减,在区间,1〕上单调递增；〔,1〔1kk\n1〔2〕当x>1时，x-〔k,〔x1〕1>0，Fx2x1〕①当k0时，F0在〕上恒成立，故F〔x〕在〔〕上单调递减；〔x〔1,区间1,〕②当k0时，令F10,1)，解得x1k12，〔x2x1〔x4k〕\n学习必备欢迎下载1且当1x1时，F〔0；当x1时，F〔x〕02124k4kx〕故F〔x〕在〔1,1〕上单调递减,在区间1〕上单调递增；22,区间14k〔14k综上得，①当k=0时，F〔x〕在区,1〕上单调递增，F〔x〕在〔〕上单调递减；间〔区间1,1②当k<0时，F〔x〕在区,1〕上单调递增，在区〔1,〕上单调递减,在区间2间〔间14k1k1〕上单调递增；③当k0时，F〔x〕在区间〕上单调递减,在区间〔,k2〔,14kk〔1,1〕上单调递增,在区〔〕上单调递减.k间1,【名师指引】求函数的单调区间或争论函数的单调性是高考的一个热点，分段落函数用留意分段处理.题型2：争论抽象函数的单调性[例2]定义在R上的函数yff0，当x＞0时，f1，且对任意的a、b∈R，有f（a+b）=f〔x〕〔0〔x，〕〕（a）·f（b）.（1）求证：f（0）=1；（2）求证：对任意的x∈R，恒有f（x）＞0；（3）求证：f（x）是R上的增函数；2（4）如f（x）·f（2x－x）＞1，求x的取值范畴.[解题思路]抽象函数问题要充分利用“恒成立”进行“赋值”，从关键等式和不等式的特点入手；2[解析]（1）证明：令a=b=0，就f（0）=f（0）.又f（0）≠0，∴f（0）=1.（2）证明：当x＜0时，－x＞0，∴f（0）=f（x）·f（－x）=1.1∴f（－x）=＞0.又x≥0时f（x）≥1＞0，f〔x〕∴x∈R时，恒有f（x）＞0.（3）证明：设x1＜x2，就x2－x1＞0.∴f（x2）=f（x2－x1+x1）=f（x2－x1）·f（x1）.∵x2－x1＞0，∴f（x2－x1）＞1.又f（x1）＞0，∴f（x2－x1）·f（x1）＞f（x1）.∴f（x2）＞f（x1）.∴f（x）是R上的增函数.22（4）解：由f（x）·f（2x－x）＞1，f（0）=1得f（3x－x）＞f（0）.又f（x）是R上的增函数，2∴3x－x＞0.∴0＜x＜3.【名师指引】解此题的关键是敏捷应用题目条件，特殊是（3）中“f（x2）=f［（x2－x1）+x1］”是证明单调性的关键，这里表达了向条件化归的策略.考点2函数的值域（最值）的求法题型1：求分式函数的最值2x2xa[例3]（2000年上海）已知函数f,x[1,〕.〔xx〕1当a时，求函数\n2f〔x〕的最小值；1[解题思路]当a1时，fx2，这是典型的“对钩函数”，欲求其最小值，可以考虑均值不等式或2x导数；〔x〕2\n学习必备欢迎下载111[解析]当a时，fx2,f'〔x〕122〔x2x2x〕x1，f〔x〕f在区间[1,〕上为增函数；0；〔x〕7f〔x〕在[1,〕上的最小值f〔1〕；区间为21【名师指引】对于函数f〔x〕2,如x0，就优先考虑用均值不等式求最小值，但要留意等号是否成x2x11立，否就会得到f〔x〕22x222〔x2x2x〕11而认为其最小值为22，但实际上，要取得等号，必需使得x，这时x[,2x〕2所以，用均值不等式来求最值时，必需留意：一正、二定、三相等，缺一不行；其次,不等式恒成立问题常转化为求函数的最值；此题考查求函数的最小值的三种通法：利用均值不等式，利用函数单调性，二次函数的配方法，考查不等式恒成立问题以及转化化归思想；题型2：利用函数的最值求参数的取值范畴2x2xa[例4]（2000年上海）已知函数f,x[1,〕.〔xx〕如对任意x[1,f〔x〕0恒成立,试求实数a的取值范畴；〕,[解题思路]欲求参数a的取值范畴，应从x[1,f〔x〕0恒成立的详细情形开头；〕,2x2xa[解析]f0在区间[1,〕上恒成立；〔xx〕2x2xa0在区间[1,〕上恒成立；2x2xa在区间[1,〕上恒成立；2函数yx2x在区间[1,〕上的最小值为3，a3即a3【名师指引】这里利用了分别参数的方法，将问题转化为求函数的最值；题型3：求三次多项式函数的最值〕1〕〔x'[例5（]09年高州中学）已知a为实数，函数f1〕〔xa)，如f0，2〔x求函〔数y\n〔x〕在[32f,1]上的最大值和最小值；[解题思路]求三次多项式函数在闭区间上的最值，应当用导数作为工具来争论其单调性；，322[解析]∵f〔0，由f〔xaxxa,f3x2ax1，1〕x〔〕x〕32a10,a2,分32f〔x〕4x1分43x\n学习必备欢迎下载1由f3〕〔x1〕得：〔〔3x〕x1当f0时，x1或x分5〔3x〕1当f0时，1x分6〔3x〕311因此，f〔x〕在区,1]和[,1]内单调递减，而在[1,]内单调递减，间[233且f极大值f〔2,f〔微小值150f〔〕〔x〕1x327〕〕50313f6,且13又f〔〕，28〔1278〕3f〔x〕,1]上的最大值f6,最小值f〔13，分10在[2〔138〕〕2【名师指引】用导数来争论其单调性和最值是高考考查的重点和热点，同时也是难点，要求考生娴熟把握用导数来争论其单调性和最值的方法和步骤；第5讲函数的奇偶性和周期性★热点考点题型探析考点1判定函数的奇偶性及其应用题型1：判定有解析式的函数的奇偶性[例1]判定以下函数的奇偶性：1x（1）f（x）=|x+1|－|x－1|；（2）f（x）=（x－1）·；1x21xx〔1〔x0〕,（3）f；（4）fx〔x|x2|2〔x〔x0〕.〕〕〕x〔1x〕[思路点拨]判定函数的奇偶性应依照定义解决，但都要先考查函数的定义域；[解析]（1）函数的定义域x∈（－∞，+∞），对称于原点.∵f（－x）=|－x+1|－|－x－1|=|x－1|－|x+1|=－（|x+1|－|x－1|）=－f（x），∴f（x）=|x+1|－|x－1|是奇函数.1x（2）先确定函数的定义域.由≥0，得－1≤x＜1，其定义域不对称于原点，所以f（x）既不是奇函数也不是1x偶函数.（3）去掉肯定值符号，依据定义判定.21x0,1x1,由得\n|x2|20,x0且x4.故f（x）的定义域为［－1，0）∪（0，1］，关于原点对称，且有x+2＞0.1x221〔x〕21x1x从而有f（x）==，∴f（－x）=2=－f（x）x22x=－xx故f（x）为奇函数.（4）∵函数f（x）的定义域是（－∞，0）∪（0，+∞），并且当x＞0时，－x＜0，∴f（－x）=（－x）［1－（－x）］=－x（1+x）=－f（x）（x＞0）.当x＜0时，－x＞0，∴f（－x）=－x（1－x）=－f（x）（x＜0）.\n学习必备欢迎下载故函数f（x）为奇函数.【名师指引】○1函数的奇偶性是函数的一个整体性质,定义域具有对称性〔即如奇函数或偶函数的定义域为D,就xD时xD〕是一个函数为奇函数或偶函数的必要条件○2分段函数的奇偶性一般要分段证明.③判定函数的奇偶性应先求定义域再化简函数解析式.题型2：证明抽象函数的奇偶性[例2]（09年山东梁山）定义在区间〔1,1〕上的函数x,y〔1,1〕，f〔x〕满意：对任意的fy都有f〔f〔〕.x〔yxxy〕〕1求证f〔x〕为奇函数；[思路点拨]欲证明f为奇函数，就要证明f〔f〔x〕，但这是抽象函数，应设法充〔xx〕〕y分利用条件“对任意的x,y〔1,1〕，fff〕”中x,y进行合理都有〔x〔y〔的〕〕xxy1“赋值”[解析]令x=y=0，就0f〔0〕+ff〔f〔0〕0〔0〕=〕∴f〔0〕=010令x∈〔－1,1〕∴－x∈〔－1,1〕xx∴f〔x〕+f〔－x〕=f〕=f〔0〕=0〔21x∴f〔－x〕=－f〔x〕∴f〔x〕在〔－1，1〕上为奇函数【名师指引】对于抽象函数的奇偶性问题，解决的关键是奇妙进行“赋值”，而抽象函数的不等式问题，要敏捷利用已知条件，特殊是f〔x1〕－f〔x2〕=f〔x1〕+f〔－x2〕考点2函数奇偶性、单调性的综合应用[例3]（普宁市城东中学09）已知奇函数f〔x〕是定义2,2〕上的减函数，f〔mf〔2m0，求在〔如11实数m的取值范畴；〕〕[思路点拨]欲求m的取值范畴，就要建立关于m的不等式，可见，只有从f〔mf〔2m0动身，所以应当利用f的奇偶性和单调性将外衣“f”脱去；11〔x〕〕〕[解析]f〔x〕是定义2,2上奇函数在〔〕对任意x〔2,2〕有fxfx\n由条件f〔mf〔2m0得f〔mf〔21〕f〔12m〕111m=〕〕〕f〔x〕是定义2,2上减函数在〔〕212mm12，解得1m22312实数m的取值范畴是m23【名师指引】利用函数的奇偶性可以求对称区间上的函数的表达式\n学习必备欢迎下载[例4]设函数f〔x〕是定义在R上的偶函数，并在区间〔－∞,0〕内单调递增，f22〔2a+a+1〕3a－2a+1.解之，得0