定量生理复习资料 11页

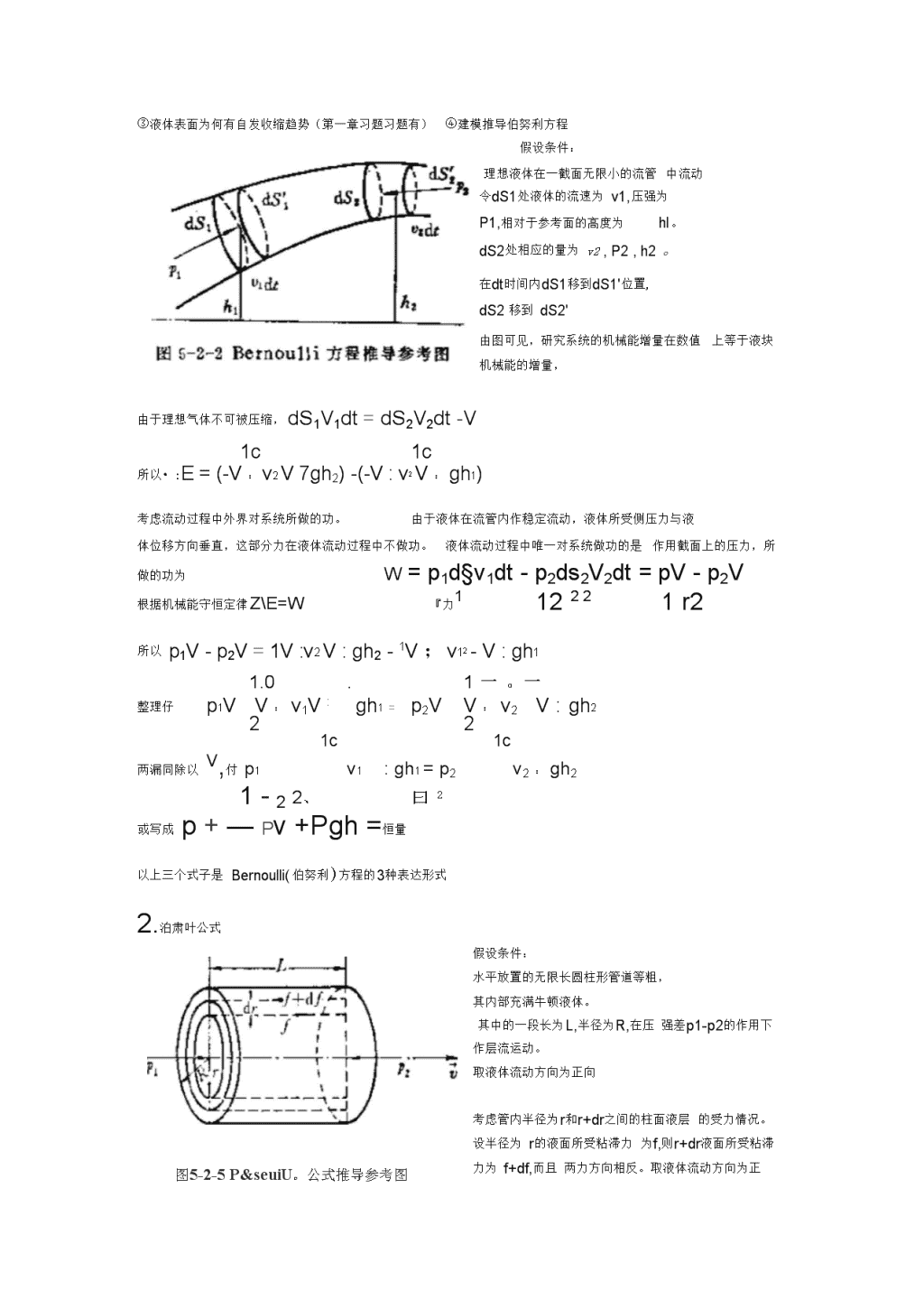
往年考题定量生理一.填空题呼吸机基础代谢率三个系统动作电位特点卡森方程心电图与心电向量环关系（一次投影二次投影）标准导联二.解释题静息电位：指细胞未受刺激时，存在于细胞膜内外两侧的外正内负的电位差基础代谢：动物处于安静、活动降至最低时的能量代谢单级导联：？雷诺系数：惯性力与单位面积液层所受的粘滞力之比牛顿液体：切应力与切应变率呈线性关系，而且切应变率趋于0时，切应力也趋于0,具有这种特性的液体流量强度、流量密度之间的关系：单位时间内通过某面积的物质总量（质量、体积或粒子数）称为流量强度单位时间内通过垂直于物质输运方向每单位面积的物质量称为流量密度三.简答1.牛顿液体内摩擦力：流体内部不同流速层之间的黏性力2.??3.大小血液在大血管中的流动状态：血液在大血管中流动时，血液的流动状态可分成两部分：中心部分（r0时，d-=0,由此求得积分常数drG=0，可得CidvdrPi-P2r2L>-rdr—jr2\n当r=R时，v=0,由此求得积分常数c=p1-p2r2—>24L中心处流速最大v0=p1—p2R2,管壁处流速最小，等于04L4.血液在大血管中流动状态如何？试简单分析为什么会产生这种状态。流动状态：已有。为什么：不同管径的血管边界层的厚度以及边界层厚度相对于管径之比不同，pl-p24L(R2-r2)边界层内平均速度梯度的大小也不同，因而粘滞力对血管内血液总的流动状态的支配作用的大小也不一样5.实际应用中怎样描述血液的粘度？谈谈你认为有哪些量影响血液的粘度，都是怎样影响的？在实际应用中常引入血液的表观粘度和相对粘度两个概念来描述血液的粘度。血液流速、管径、血细胞体积，都会影响血液粘度。其中血液流速越快、血细胞体积越小，血液的粘度越小。对于小血管，管径越小，血液的粘度减小，这与大、中血管中随管径的减小血液粘度显著增大的特点正好相反。6.考虑管径的厚度的情况下，血管的跨壁压强和周向张力如何计算？试建模并给出推导。跨壁压强：周向张力：设管壁的弹T,「0,扩张后的平均管径为r,血管壁的厚度为h,管壁周向每单位长度的张力为则可得血管形变量AL=2nAr=2n（r-「0），血管壁内周向应力为又因为CTCTE二一二△LL0L。二E口「0，所以T=E匚10h「0Eh（「-r。）TEh（r-r0）单位长周向张力一：此时血管的跨壁压为pTM=一=2「。rr。第六章心电1.心电图和心电向量环之间有什么关系？心电图是平面心电向量环在各导联轴上第二次投影所产生的曲线图形2.三种标准导联和三种加压单极肢体导联各是怎样连接的？标准I联接右上肢（—）——左上肢（+）;标准n联接右上肢（―）——左下肢（+）；标准出联接左上肢（一）——左下肢（+）。aVR导联右上肢为探查电极，左上、左下肢体联接于一点作为另一极aVL导联左上肢为探查电极，右上、左下肢体联接于一点作为另一极\naVF导联左下肢为探查电极，左上、右上肢体联接于一点作为另一极1.心室肌中普通心肌细胞的动作电位是如何变化的？快速复极3末期，膜电位降至静息电位如何变化：快速复极3末期，膜电位降至静息电位，之后膜电位自动出现缓慢升高的现象。2.人工心脏电起搏的原理是什么？起搏系统由哪些单元组成？用一定形式的脉冲电流刺激心脏，使心脏按一定频率有效收缩单元：低频脉冲发生器刺激电极及导线电源第七章呼吸力学外呼吸：外界空气与肺泡之间以及肺泡与肺毛细血管血液之间的气体交换。内呼吸：组织细胞与组织毛细血管血液之间的气体交换。呼吸机：能够将空气、氧气或空气-氧气混合气压入肺内，产生或辅助患者的呼吸动作，使肺间歇性膨胀，达到增强和改善呼吸功能、减轻或纠正缺02与CO2滞留的目的的装置上提到*拉普拉斯公式：建立模型图7-2-l(b),其假设条件如下小面元ABCD其x方向曲率，半径为Rl,y方向曲率半径为R2,表面张力系数为液体表面张力T引起的附加压强为Ps,将小面元ABCD上提到面AB'C'D',dz为沿径向的增量。则为反抗表面张力的作用将小面元ABCDABCD',所做的功为dS=(ydx十xdy)它也等于附加压强与体积增量的乘积，即dS=PsdV=Psxydz由于扩张过程程中立体角未变，所以xdxxxo-m—>dx=dz，RidzRiR1*ydyy.y.—=—_、dy=dzRz+dzR2R2上式称为液体表面张力附加压强的拉普拉斯公式