自控复习资料_分析 13页

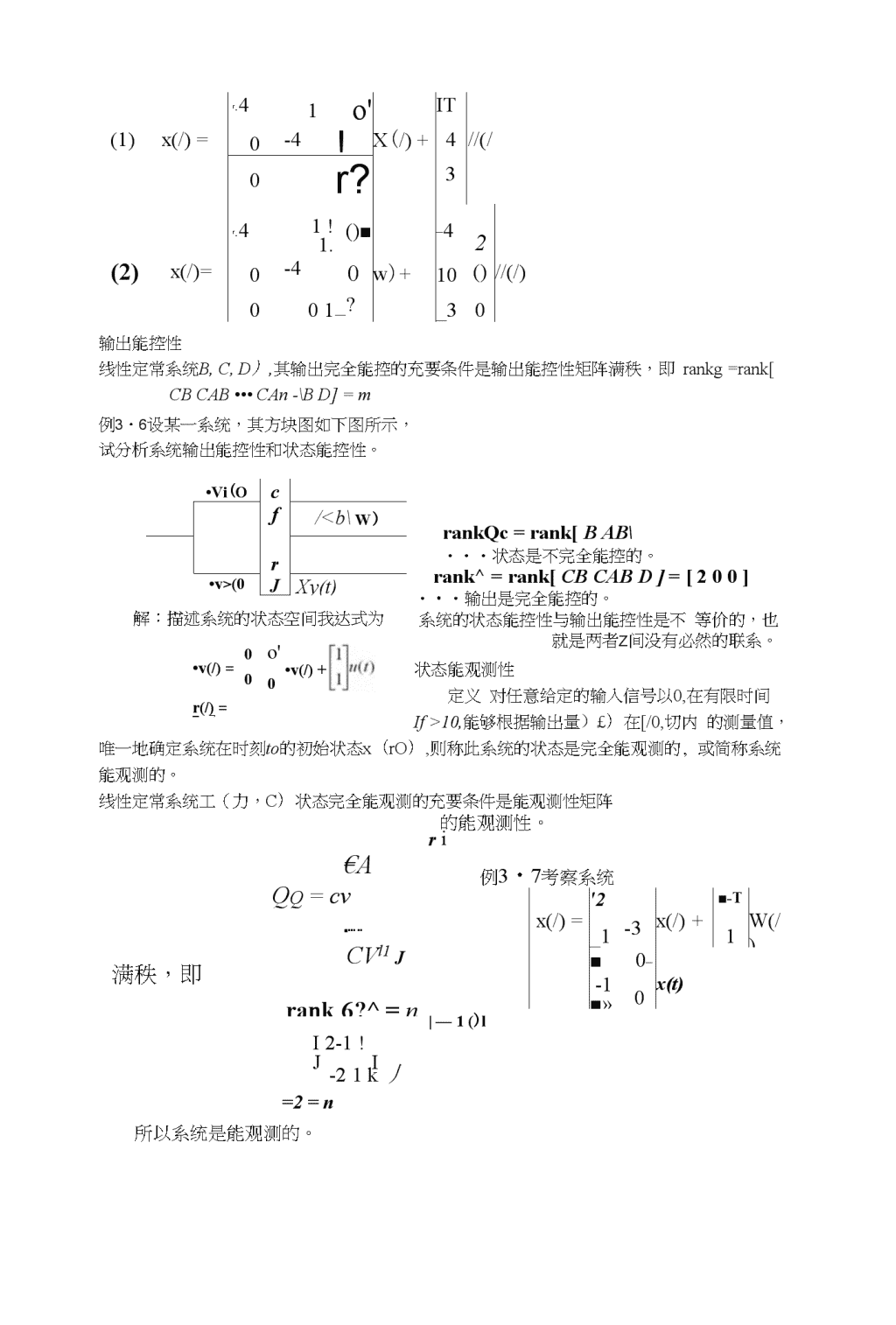
线性系统能控性和能观测性能控性，指的是控制作用对•被控系统状态进行控制的可能性；能观测性，则反映由系统输出的量测值确定系统状态的对能性。状态能控性定义：若系统2W),B(小对初始时刻/0,存在另一时刻r/(r/>/0),对心时刻的初始状态x(rO)=AO,可以找到一个容许控制“(/),能在有限时间厂旳内把系统从初态曲0)转移至任意指定的终态x(z/),那么就称系统在/0时刻的状态x(/0)是能控的。若系统在状态空间小的每一个状态都能控，那么就称系统在(/0,/)时间间隔内是状态完全能控的，简称状态能控的或能控系统。若系统存在某一个状态兀(/0)不满足上述条件，则此系统称为不能控系统。线性定常连续系统3)其状态完全能控的充要条件是其能控性矩阵Qc=[BABA2B…An-\B]的秩为巾,即rank0c=n例设系统的状态方程为'132■■21x(t)=020W)+11u(t)013-1-1判断其状态能控性。解：系统的能控性矩阵为2IQC=[BAB-11322244-2-■2—4一4rankCJc-2工〃所以系统状态不完全能控。设线性定常连续系统ZW，3)具有两两相界的特征值，则其状态完全能控的充要条件，是系统经线性变换后的对角线矩阵中，不包含元素全为零的行。若线性连续系统工(儿3)冇相重的特征值时，即/为约当形时，则系统能控的充要条件是:(1)输入矩阵3屮对应于互异的特征值的各行，没有一行的元素全为零；(2)输入矩阵3中与每个约当块最后一行相对应的各行，没有一行的元素全为零。\n「-41o'IT(1)x(/)=0-4!(0■JXy(t)■解：描述系统的状态空间我达式为00•v(/)=r(/)=■r了o'•v(/)+0■rankQc=rank[BAB\・・・状态是不完全能控的。rank^=rank[CBCABD]=[200]・•・输出是完全能控的。系统的状态能控性与输出能控性是不等价的，也就是两者Z间没有必然的联系。状态能观测性定义对任意给定的输入信号以0,在有限时间If>10,能够根据输岀量）£）在[/0,切内的测量值，唯一地确定系统在时刻to的初始状态x（rO）,则称此系统的状态是完全能观测的,或简称系统能观测的。例3・7考察系统L'2■-Tx(/)=_1-3x(/)+1W(/)■10_-1■»0x(t)线性定常系统工（力，C）状态完全能观测的充要条件是能观测性矩阵满秩，即€AQq=cv■•••••CVl1Jrank6?^=n的能观测性。ri|—1()lI2-1!JI-21k丿=2=n所以系统是能观测的。\n设线性定常连续系统为(力，C)具冇互不相同的特征值，则其状态完全能观测的充要条件，是系统经线性非奇异变换后的对角标准形Ax(/)»、Ax(0=y(/)=Cx(z)屮，C不包含全为零的列。设线性定常连续系统为(力，C)具冇璽特征值，则其状态完全能观测的充要条件，是系统经线性非奇异变换后的约当标准形rj1_x(r)=.x(z)■y(0=Cx(z)中，和每个约当块力(/=1,2,k)首行和对应的C的所有那些列，英元素不全为零。例34分析下列系统的状态能观测性I(1)-5-V(/)]•(/)=[o45]x(/)-1-7(2)=-5x(t)(3)\nx(/)=x(t)=-2.*(/)XO=j11[1o-011]00■1x(/)「202\33-03x(/)0•r(z)=0\n对偶性原理系统El状态完全能控（完全能观测）的充要条件与其对偶系统工2状态完全能观测（完全能控）的充要条件相同。根据这一•原理，-•个系统的状态完全能控性（能观测性）就可以借助其对偶系统的状态完全能观测性（能控性）来研究。系统的能控性和能观测性与传递函数阵的关系前已述及，系统的能控性和能观测性是现代控制理论中两个重要的基本概念。而传递函数矩阵概念，冃前已被广泛用于控制工程中，那么它们Z间是否存在内在联系呢？回答是肯定的。为了阐明它们之间的联系，首先应该对不完全能控，或者不完全能观测系统进行结构分解，即把系统中不能控或不能观测的部分同系统的能控与能观测部分区分开来，要做到这一点，一般可用线性变换来解决。3.6.1系统的结构分解1.系统按能控性分解L•■■〜〜"144+■-.v,(r)L.■U0&■■■■■■■0■■y(t)=C2Jv(r)则必存在一个非奇能将系统变为-v(/)=Tcx(t)//(/)卜心）=」1工（/）+「无卫⑴+〃"⑴［y1（r）=C1x1（r）定理设有號状态不完全能控线性定常系统工（」，0,n\nk（2c=k