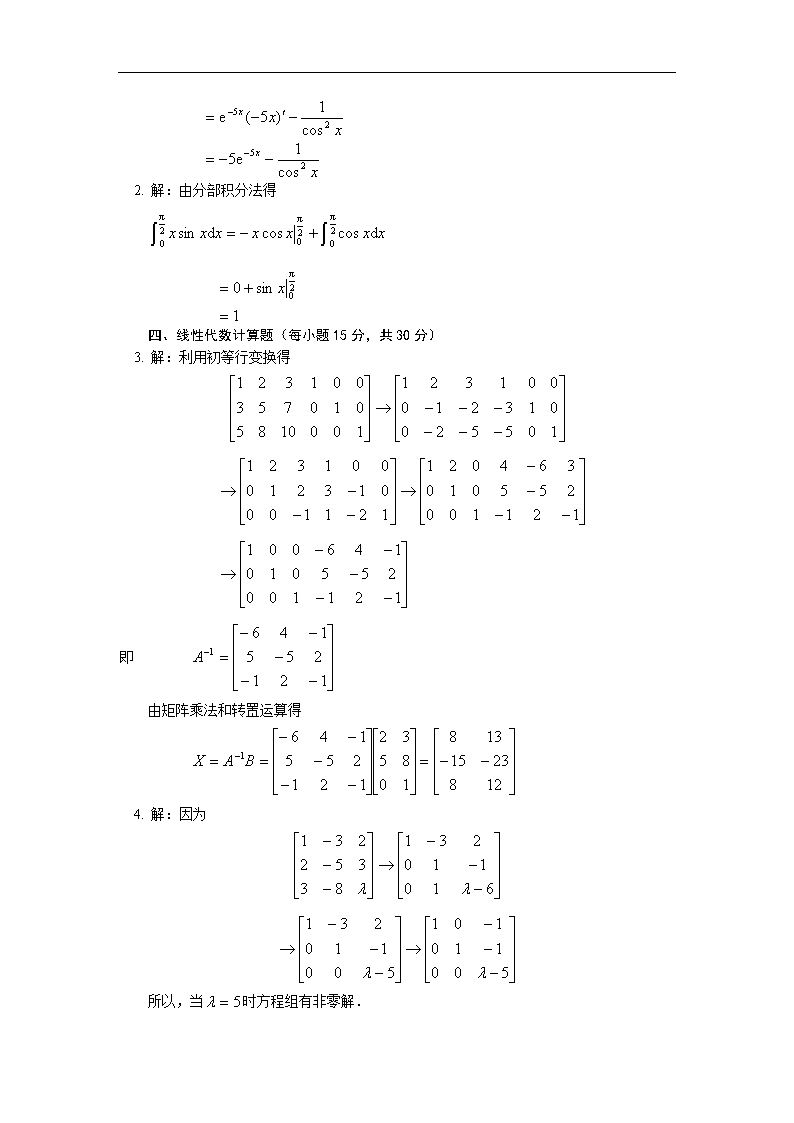经济数学复习资料 19页

经济数学基础（10秋）模拟试题（一）2010年12月一、单项选择题（每小题3分，本题共15分）　1.下列各函数对中，（D）中的两个函数相等．　　(A)，　(B)，+1　　(C)，　(D)，　2.下列结论中正确的是（D）．(A)使不存在的点x0，一定是f(x)的极值点(B)若(x0)=0，则x0必是f(x)的极值点(C)x0是f(x)的极值点，则x0必是f(x)的驻点(D)x0是f(x)的极值点，且(x0)存在，则必有(x0)=0　3.在切线斜率为2x的积分曲线族中，通过点（1,4）的曲线为（　C）．　　(A)　　(B)　　(C)　　　　(D)　4.设是矩阵，是矩阵，且有意义，则是（A）矩阵．　　(A)　　(B)　　(C)　　(D)5.若元线性方程组满足秩，则该线性方程组（B）．　　(A)有无穷多解　　　　　　　(B)有唯一解　　(C)有非0解　　　　　　　(D)无解二、填空题（每小题3分，共15分）　1.函数的定义域是　　　　　．　2.曲线在处的切线斜率是　　　　　　．　3.　　　　　．　4.若方阵满足　　　　　　，则是对称矩阵．\n　5.线性方程组有解的充分必要条件是　　秩秩　　　．三、微积分计算题（每小题10分，共20分）1.设，求．　2.计算定积分．四、线性代数计算题（每小题15分，共30分）　3.已知，其中，求．4.设齐次线性方程组，为何值时，方程组有非零解？在有非零解时求其一般解．五、应用题（本题20分）设某产品的固定成本为36（万元），且边际成本为（万元/百台）．试求产量由4百台增至6百台时总成本的增量，及产量为多少时，可使平均成本达到最低．经济数学基础（10秋）模拟试题（一）答案（供参考）2010年12月　　一、单项选择题（每小题3分，本题共15分）　　1.D　2.D　3.C　4.A　5.B　　二、填空题（每小题3分，本题共15分）　　1.　2.　3.　4.　5.秩秩　　三、微积分计算题（每小题10分，共20分）　1.解：由微分四则运算法则和微分基本公式得　　　　　\n　2.解：由分部积分法得　　四、线性代数计算题（每小题15分，共30分）3.解：利用初等行变换得　　　　　　　　　　　　　　即　　　　　　　　　　　由矩阵乘法和转置运算得　　　　　　4.解：因为所以，当时方程组有非零解．\n一般解为　　　　　　　　（其中为自由未知量）　　五、应用题（本题20分）解：当产量由4百台增至6百台时，总成本的增量为==100（万元）又==令，解得．又该问题确实存在使平均成本达到最低的产量，所以，当时可使平均成本达到最小．经济数学基础（10秋）模拟试题（二）2010年12月一、单项选择题（每小题3分，共15分）1．设，则（）．A．B．C．D．2．已知，当（）时，为无穷小量．　　A．　B．　　C．　　　D．3.若是的一个原函数，则下列等式成立的是()．A．B．C．D．4．以下结论或等式正确的是（）．A．若均为零矩阵，则有B．若，且，则C．对角矩阵是对称矩阵D．若，则5．线性方程组解的情况是（）．　　A.有无穷多解　　B.只有0解　　C.有唯一解　　D.无解\n二、填空题（每小题3分，共15分）6．设，则函数的图形关于　　　　　对称．7．函数的驻点是．8．若，则．9．设矩阵，I为单位矩阵，则＝．10．齐次线性方程组的系数矩阵为则此方程组的一般解为．三、微积分计算题（每小题10分，共20分）11．设，求．12．计算积分．四、代数计算题（每小题15分，共50分）13．设矩阵，求解矩阵方程．14．讨论当a，b为何值时，线性方程组无解，有唯一解，有无穷多解.五、应用题（本题20分）15．生产某产品的边际成本为(q)=8q(万元/百台)，边际收入为(q)=100-2q（万元/百台），其中q为产量，问产量为多少时，利润最大？从利润最大时的产量再生产2百台，利润有什么变化？\n经济数学基础（10秋）模拟试题（二）答案（供参考）2010年12月一、单项选择题（每小题3分，共15分）1．C2.A3.B4.C5.D二、填空题（每小题3分，共15分）6.y轴7.x=18.9.10．，，是自由未知量〕三、微积分计算题（每小题10分，共20分）11．解：因为所以12．解：四、线性代数计算题（每小题15分，共30分）13．解：因为即所以，X===14．解：因为\n所以当且时，方程组无解；当时，方程组有唯一解；当且时，方程组有无穷多解.五、应用题（本题20分）15.解：(q)=(q)-(q)=(100–2q)–8q=100–10q令(q)=0，得q=10（百台）又q=10是L(q)的唯一驻点，该问题确实存在最大值，故q=10是L(q)的最大值点，即当产量为10（百台）时，利润最大.又D18分即从利润最大时的产量再生产2百台，利润将减少20万元.20分经济数学基础（模拟试题1）一、单项选择题（每小题3分，共15分）1．函数的定义域是（）．A．B．C．D．且2．函数在x=0处连续，则k=()．A．-2B．-1C．1D．23．下列不定积分中，常用分部积分法计算的是（）．A．B．C．D．4．设A为矩阵，B为矩阵，则下列运算中（）可以进行．A．ABB．ABTC．A+BD．BAT\n5.设线性方程组的增广矩阵为，则此线性方程组的一般解中自由未知量的个数为（）．A．1B．2C．3D．4二、填空题（每小题3分，共15分）6．设函数，则．7．设某商品的需求函数为，则需求弹性．8．积分．9．设均为阶矩阵，可逆，则矩阵方程的解X=．10.已知齐次线性方程组中为矩阵，则．三、微积分计算题（每小题10分，共20分）11．设，求．12．计算积分．四、代数计算题（每小题15分，共50分）13．设矩阵A=，计算．14．求线性方程组的一般解．五、应用题（本题20分）15．已知某产品的边际成本为(万元/百台)，为产量(百台)，固定成本为18(万元)，求最低平均成本.模拟试题1答案及评分标准\n（供参考）一、单项选择题（每小题3分，共15分）1．D2.C3.C4.A5.B二、填空题（每小题3分，共15分）6．7.8.09.10．3三、微积分计算题（每小题10分，共20分）11．解：7分10分12．解：10分四、线性代数计算题（每小题15分，共30分）13．解：因为5分且13分所以15分14．解：因为增广矩阵10分所以一般解为（其中是自由未知量）15分\n五、应用题（本题20分）15．解：因为总成本函数为=5分当=0时，C(0)=18，得c=18，即C()=8分又平均成本函数为12分令，解得=3(百台)17分该问题确实存在使平均成本最低的产量.所以当x=3时，平均成本最低.最底平均成本为(万元/百台)20分经济数学基础（模拟试题2）一、单项选择题（每小题3分，共15分）1．下列各函数对中，（）中的两个函数相等．A．，B．，+1C．，D．，2．当时，下列变量为无穷小量的是（）．A．B．C．D．3．若，则f(x)=（）．A．B．-C．D．-4．设是可逆矩阵，且，则（）.　　A．B．C．D．\n5．设线性方程组有无穷多解的充分必要条件是（）．A．B．C．D．二、填空题（每小题3分，共15分）6．已知某商品的需求函数为q=180–4p，其中p为该商品的价格，则该商品的收入函数R(q)=．7．曲线在点处的切线斜率是．8．．9．设为阶可逆矩阵，则(A)=．10．设线性方程组，且，则时，方程组有唯一解．三、微积分计算题（每小题10分，共20分）11．设，求．12．计算积分．四、代数计算题（每小题15分，共50分）13．设矩阵A=，B=，计算(AB)-1．14．求线性方程组的一般解．五、应用题（本题20分）15．设生产某种产品个单位时的成本函数为：（万元）,求：（1）当时的总成本、平均成本和边际成本；（2）当产量为多少时，平均成本最小？模拟试题2参考解答及评分标准\n一、单项选择题（每小题3分，共15分）1．D2.A3.C4.C5.B二、填空题（每小题3分，共15分）6.45q–0.25q27.8.09.n10．三、微积分计算题（每小题10分，共20分）11．解：因为所以12．解：四、线性代数计算题（每小题15分，共30分）13．解：因为AB==(ABI)=所以(AB)-1=14．解：因为系数矩阵所以一般解为（其中，是自由未知量）五、应用题（本题20分）15．解：（1）因为总成本、平均成本和边际成本分别为：\n，，．所以，，，．（2）令，得（舍去）．因为是其在定义域内唯一驻点，且该问题确实存在最小值，所以当20时，平均成本最小.经济数学基础（模拟试题3）一、单项选择题（每小题3分，共15分）1．若函数，则()．A．-2B．-1C．-1.5D．1.52．曲线在点（0,1）处的切线斜率为（）．A．B．C．D．3．下列积分值为0的是（）．A．B．C．D．4．设，，是单位矩阵，则＝（）．A．B．C．D．\n5.当条件（）成立时，元线性方程组有解．A.B.C.D.二、填空题（每小题3分，共15分）6．如果函数对任意x1,x2，当x1