地理建模复习资料 4页

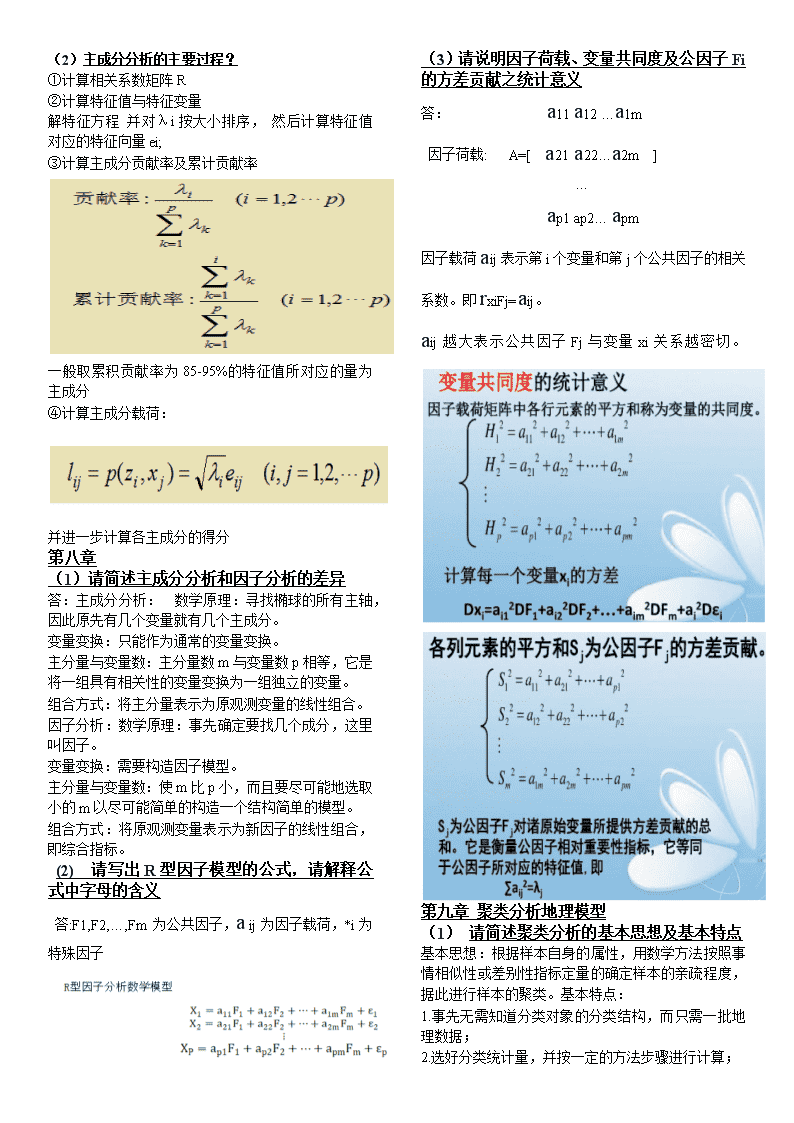
第一章（1）模型、模式、模拟与地理模型的内涵与相互关系模型：是对现实世界中的实体或现象的抽象或简化，是对实体或现象中的最重要的构成及其相互关系的表述。 模式：经检验有效的、被广泛接受的模型就称为模式；也可称为标准或样板。 模拟：是一种实验方法，是模型的构建和模型应用过程。模拟首先是针对特定的研究对象构建一个模型，然后利用该模型对研究对象进行各种实验，其目的是为了理解研究对象的行为，评估在一定的限制条件下研究对象的各种变化和不同对策所产生的结果。地理模型是地理建模的结果。（2）什么是概念模型，物理模型，数学模型概念模型：是指利用科学的归纳方法，以对研究对象的观察、抽象形成的概念为基础，建立起来的关于概念之间的关系和影响方式的模型。 物理模型：又称实体模型，是现实世界在尺寸上缩小或放大后构成的相似体。 数学模型：是用数学方程（通常是一些代数方程和微分方程的组合）来描述现实世界结构和特性的模型。（3）建模的基本过程包括哪些内容了解问题、明确建模目的；收集资料，确定建模类型、建立要素关系。确定建模方法（物理或数学的）；选择变量参数；模拟运行模型模型检验包括模型验证和模型确认模型验证：检查数学公式和计算机程序以保证没有运算方面的问题，目的是保证概念模型的数量化是直接和正确的。模型确认：确定模型在其既定应用范围内运行的结果与其相对应的现实世界相吻合。常涉及到模型结构和变量间关系合理性检验、模型输出与实际值的比较、模型的敏感性分析、模型的不确定性分析。模型应用是指设计和执行模拟实验，分析、综合、解释模型，并交流模型结果和征求改进意见。第二章（1）地理数据根据测量尺度分为哪几类？间隔尺度：以单位距离为间隔来表达地理要素，但不同的性质可采用不同的标准；但其相对关系不会变；一般没有自然0值，如高程。比例尺度：以连续量来表示地理要素，需要规定一个0基点。有序数据：表示次序关系，不表示具体数量。名义尺度数据：可用名字或符号表示地理要素的类型的数据；如土地利用类型。（2）数据变换的目的是什么？使变量尽可能为正态分布。统一变量的数据尺度。使变量间的非线性关系转换为线性关系。用新的、数目少的相互独立的变量代替相互联系的原始变量方便用简单自然的方式进行解释帮助理解数据的特征。第三章（1）统计相关建模的内容与方法统计建模是以计算机统计分析软件为工具，利用各种统计分析方法对批量数据建立统计模型和探索处理的过程，用于揭示数据背后的因素，诠释社会经济现象，或对经济和社会发展作出预测或判断。 统计相关建模的目的：1.变量间相关性研究2.形成科学的成因假设3.预测4.数据简化或结构化 建模的步骤：1.数据整理2.数据预处理3.模型计算4.模型检验5.模型解释和应用（2）回归分析中，随机干扰项的意义是什么？随机干扰项又称残差或误差，是因变量回归结果与原始值的差。回归分析中，干扰项被认为是从模型中省略下来的而又集中地影响Y的其它变量的替代物引入残差的理由：理论的含糊性；数据欠缺；核心变量与周边变量；人类行为的随机性；替代变量问题：如数据误差；简约性原则；错误的函数形式。第五章（1）逐步回归的意义是什么？目的是什么？在众多因子中，先对因素进行检验，使引入的因素均具有显著的意义，且不重复逐步回归研究的问题就是讨论在众多因子中，优选出影响最大的因子，从而建立最优线性回归方程。（2）逐步回归的基本过程有哪些？1、数据变换处理与相关矩阵2、确定F检验值3、逐步回归计算4、建立逐步回归方程5、显著性检验第六章（1）判别分析的目的是什么？①判别地理类型的归属②确定不同地理类型间的界线（2）判别分析的主要准则有哪些?①费歇尔准则：先对样本进行投影（线性组合）再进行判别分类的方法；适用于两组判别。②贝叶斯准则：将地理数据分为多组，计算未知地理类型或区域归属于各已知类型的概率值，再进行分类的方法；适用于多组分类③其它分类：最小二乘准则、KULLBACK准则等第七章（1）正交变换的特征有哪些?①保持向量长度不变②保持两个非零向量的夹角不变③保持正交性不变\n（1）主成分分析的主要过程？①计算相关系数矩阵R②计算特征值与特征变量解特征方程并对λi按大小排序，然后计算特征值对应的特征向量ei;③计算主成分贡献率及累计贡献率一般取累积贡献率为85-95%的特征值所对应的量为主成分④计算主成分载荷：并进一步计算各主成分的得分第八章（1）请简述主成分分析和因子分析的差异答：主成分分析：数学原理：寻找椭球的所有主轴，因此原先有几个变量就有几个主成分。变量变换：只能作为通常的变量变换。主分量与变量数：主分量数m与变量数p相等，它是将一组具有相关性的变量变换为一组独立的变量。组合方式：将主分量表示为原观测变量的线性组合。因子分析：数学原理：事先确定要找几个成分，这里叫因子。变量变换：需要构造因子模型。主分量与变量数：使m比p小，而且要尽可能地选取小的m以尽可能简单的构造一个结构简单的模型。组合方式：将原观测变量表示为新因子的线性组合，即综合指标。(2)请写出R型因子模型的公式，请解释公式中字母的含义答:F1,F2,…,Fm为公共因子，aij为因子载荷，*i为特殊因子（3）请说明因子荷载、变量共同度及公因子Fi的方差贡献之统计意义答：a11a12…a1m因子荷载:A=[a21a22…a2m]…ap1ap2…apm因子载荷aij表示第i个变量和第j个公共因子的相关系数。即rxiFj=aij。aij越大表示公共因子Fj与变量xi关系越密切。第九章聚类分析地理模型（1）请简述聚类分析的基本思想及基本特点基本思想：根据样本自身的属性，用数学方法按照事情相似性或差别性指标定量的确定样本的亲疏程度，据此进行样本的聚类。基本特点：1.事先无需知道分类对象的分类结构，而只需一批地理数据；2.选好分类统计量，并按一定的方法步骤进行计算；\n3.自然地、客观地得出一张分类系统图。简述系统聚类分析的基本思想答：系统聚类分析是聚类分析中应用最广泛的一种方法，凡是具有数值特征的变量和样品都可以采用系统聚类法。选择不同的距离和聚类方法可获得满意的数值分类效果。系统聚类法是把个体逐个地合并成一些子集，直至整个总体都在一个集合之内为止。（1）简述动态聚类分析的基本思想及步骤答：动态聚类法又称逐步聚类法，其基本思路是，开始按照一定的方法选取一批凝聚点，然后将样品向最近的凝聚点凝聚，这样由点凝聚成类，得到初始分类。初始分类不一定合理，然后按照最近距离院子修改不合理的分类，直到分类比较合理为止，这样形成一个最终的分类结果。计算步骤：1.先将原始数据进行标准化处理。2.选择预定数量的凝聚点，对样品进行初始分类。3.计算每一类的重心，该重心作为新的凝聚点，直到某一次计算的重心与原来的凝聚点完全相同，否则将重复进行。（2）简述模糊聚类分析的基本思想及步骤答：基本思想：1.用相似性尺度来衡量事物的亲疏程度，并以此来实现分类。2.考虑二维坐标系上有散落的许多点，这时需要对散点进行合理分类，就需要聚类方面的知识。具体步骤：1.对原始数据进行变换处理，变换的思想和方法等同于系统聚类分析，如标准化变换、规格化变换、对数变换等。2.计算模糊相似性矩阵。3.获得模糊分类关系。4.对地理系统的模糊集进行模糊聚类。第十章地理系统线性规划与模拟（1）写出线性规划的一般型数学模型和标准型数学模型答：一般模型：标准模型：简述一般线性规划化为标准形式的方法答：1.目标函数为极小化。2.约束条件为不等式。3.决策变量有非正约束。4.决策变量xj符号不受限制。5.决策变量有上下界。（2）简述线性规划图解法的步骤答：第一步：在平面坐标系中，给出各约束条件的图形，并确定出可行域。第二步：在可行域内做出目标函数的某一直线，并将该直线沿目标函数取优的方向平行移动，最后相触的顶点为最优点。第三步：联立通过最优点的方程得出最优解。第四步：将最优解代入目标函数得出最优值。第十二章层次分析法地理模型（1）什么是层次分析法，它适合于解决什么问题？答：层次分析法综合定性与定量分析，模拟人的决策思维过程来对多因素复杂系统，特别是难以定量描述的社会系统进行分析。它最适宜于解决那些难以完全用定量方法进行分析的公共决策问题。（2）判断矩阵满足什么条件才能满足完全一致性答：所谓判断矩阵的一致性，即判断矩阵是否满足如下关系：aij=aik/ajki，j，k=1,2，…，n上式完全成立称判断矩阵具有完全一致性，此时矩阵的最大特征根λMax=n，其余特征根均为零。（3）简述层次分析法的计算步骤答：1、建立层次结构模型。2、构造判断矩阵。3、层次单排序。4、层次总排序。\n5、一致性检验。（1）何谓层次分析法的一致性检验？答：为评价层次总排序的计算结果的一致性如何，需要计算与单排序类似的检验量。CI为层次总排序一致性指标；RI为层次总排序平均随机一致性指标；CR为层次总排序随机一致性比例：CR=CI/RI，当CR<=0.10时，我们认为层次总排序的计算结果具有满意的一致性。补充：模糊数学模型（1）简述精确性、模糊性和随机性答：精确性：非此即彼性，二维逻辑【0,1】模糊性：亦此亦彼性，连续的多值逻辑【0,1】随机性：描述事物发生的不确定性。（2）何谓模糊等价关系，需满足什么条件？定义.模糊关系R∈F(U×U),满足（1）自反性：R(u,u)=1;（2）对称性：R(u,v)=R(v,u);（3）传递性：R2⊆R则称R为模糊等价关系（3）什么叫最大-最小、最大积复合运算例：设有关系R,和S，按照最大-最小复合、最大积复合求R=S=最大最小符合（M(∧,∨)）U1x1,z1=maxmin0.1,0.5,min0.6,0.7,min1.0,0.5,min0.7,0.1=0.6以此类推T=0.60.40.70.70.40.6最大积复合:U1x1,z1=max0.1*0.5,0.6*0.7,1.0*0.5,0.7*0.1=0.5以此类推T=0.50.240.60.560.320.54（4）对某教师讲课质量进行综合评定。已知因素集合U={教材使用熟练，逻辑性强，启发性强，语言生动，板书整齐}，评语集合V={很好，较好，一般，不好}。权重分配为A=（0.3，0.2，0.2，0.2,，0.1）评判矩阵得出综合评判如下对结果进行归一化评判结果表明，对该教师的课堂教学认为“很好”的占35%，“较好”的占29%，“一般”的占24%，“不好”的占12%，根据最大隶属原则，结论是“很好”。