重积分复习资料 64页

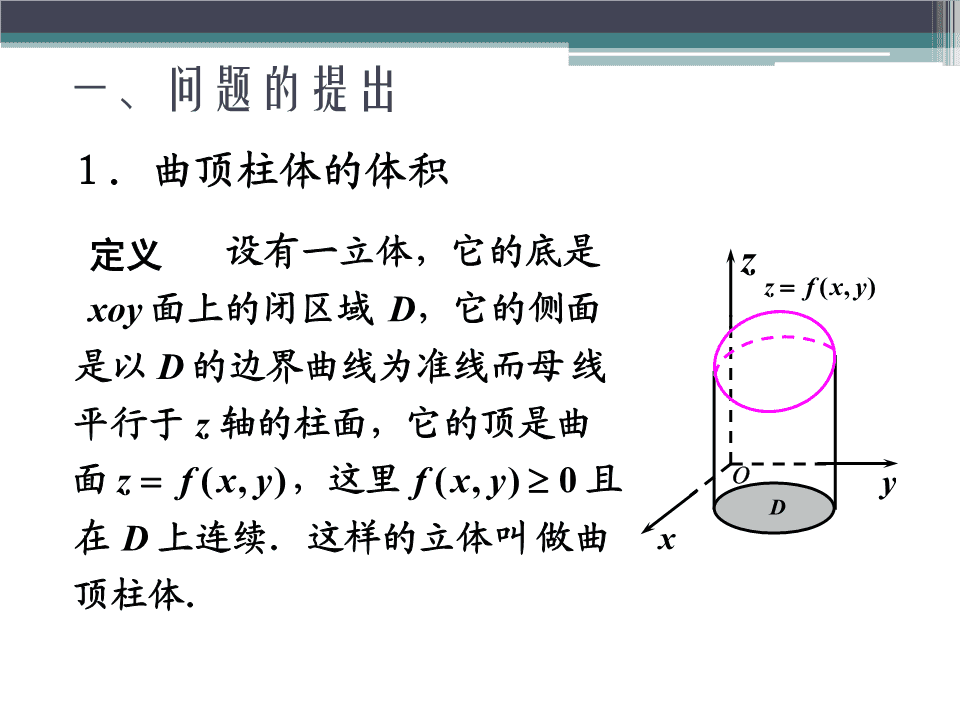
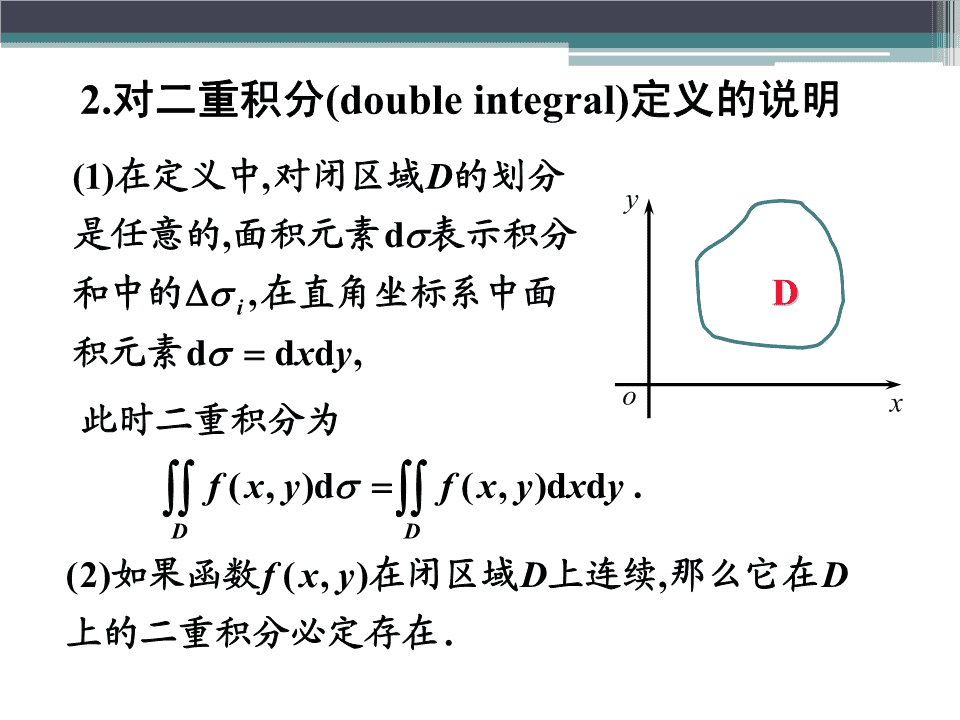
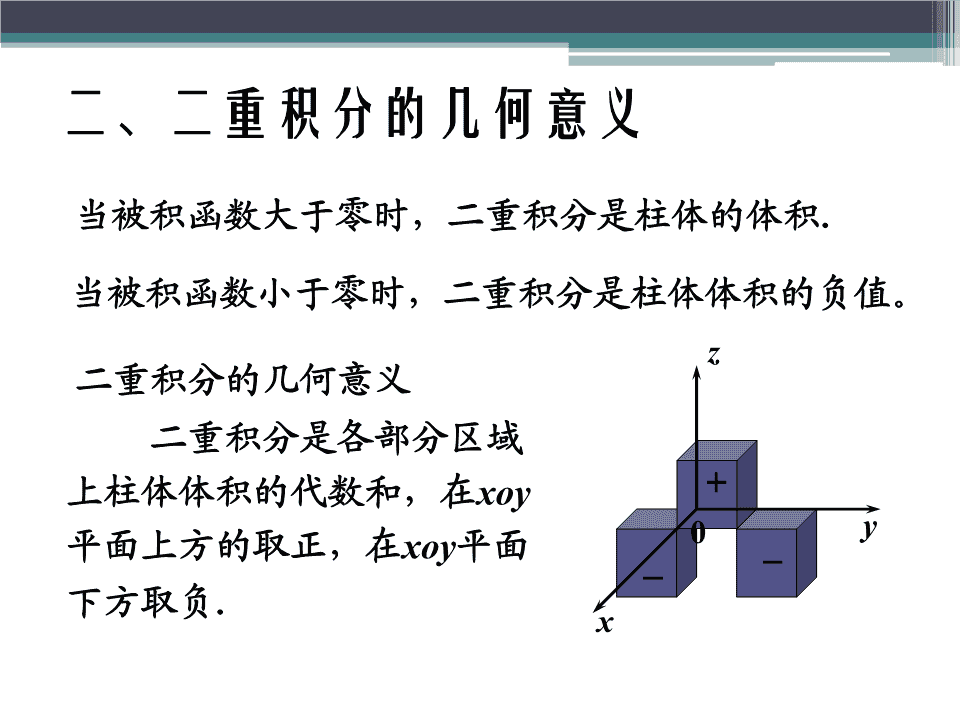
一、问题的提出１．曲顶柱体的体积定义设有一立体，它的底是zz=f(x,y)xoy面上的闭区域D，它的侧面是以D的边界曲线为准线而母线平行于z轴的柱面，它的顶是曲面z=f(x,y)，这里f(x,y)≥0且oyD在D上连续．这样的立体叫做曲x顶柱体．\n2.对二重积分(doubleintegral)定义的说明)1(在定义中,对闭区域D的划分y是任意的,面积元素dσ表示积分和中的Δσ,在直角坐标系中面DDi积元素dσ=dxdy,ox此时二重积分为∫∫f(x,yd)σ=∫∫f(x,yd)xdy.DD)2(如果函数f(x,y)在闭区域D上连续,那么它在D上的二重积分必定存在.\n二、二重积分的几何意义当被积函数大于零时，二重积分是柱体的体积．当被积函数小于零时，二重积分是柱体体积的负值。z二重积分的几何意义二重积分是各部分区域+上柱体体积的代数和，在xoy0y平面上方的取正，在xoy平面−−下方取负．x\n例1根据二重积分的几何意义判断下例积分的值.222222∫∫a−x−ydσ,D:x+y≤a，D222解投影区域为圆域D:x+y≤a，222被积函数为半球面z=a−x−y.z由二重积分的几何意义，得322214πa∫∫a−x−ydσ=⋅23DOy23=πa.3x\n三、二重积分的性质性质１当k为常数时，∫∫kf(x,yd)σ=k∫∫f(x,yd)σ.DD性质２∫∫[f(x,y)±g(x,y)]dσD=∫∫f(x,yd)σ±∫∫g(x,yd)σ.DD\n(D=D+D,)性质３对积分区域具有可加性12∫∫f(x,yd)σ=∫∫f(x,yd)σ+∫∫f(x,yd)σ.DD1D2性质４若为ΩD的面积，Ω=∫∫1⋅dσ=∫∫dσ.DD性质５若在D上有f(x,y)≤g(x,y),则有∫∫f(x,yd)σ≤∫∫g(x,yd)σ.DD特殊地∫∫f(x,yd)σ≤∫∫f(x,yd)σ.DD\n性质６设m、M是函数f(x,y)在D上的最大值和最小值,σ为D的面积,则在D上mσ≤∫∫f(x,yd)σ≤MσD（二重积分估值不等式）性质７如果函数f(x,y)在D上连续,σ为D的面积,则在D上至少存在一点(ξ,η),使得∫∫f(x,yd)σ=f(ξ,η)⋅σ.D（二重积分中值定理）\n四、二重积分计算公式如果积分区域D:ϕ(x)≤y≤ϕ(x),a≤x≤b,12其中函数ϕ(x),ϕ(x)∈C[a,b].12y=ϕ(x)y2Dx型平面区域(x型区域)y=ϕ(x)1Oabx特点:穿过D内部且垂直于x轴的直线与D的边界相交不多于两点.\ny=ϕ(x)y2Dy=ϕ(x)1Oabx情况一:若积分区域D={(x,y)ϕ(x)≤y≤ϕ(x),a≤x≤b},12bϕ2(x)则∫∫f(x,yd)σ=∫dx∫f(x,yd)y.aϕ1(x)D\n如果积分区域D:ψ(y)≤x≤ψ(y),c≤y≤d,12其中函数ψ(y),ψ(y)∈C[c,d].12ydx=ψ(y)2Dy型平面区域(y型区域)x=ψ(y)1cOx特点:穿过D内部且垂直于y轴的直线与D的边界相交不多于两点.\nydx=ψ(y)2Dx=ψ(y)1cOx情况二：若积分区域D={(x,y)ψ(y)≤x≤ψ(y),c≤y≤d},12dψ2(y)则∫∫f(x,yd)σ=∫dy∫f(x,yd)x.cψ1(y)D\nyⅡ若区域如图，则必须分割.Ⅰ在分割后的三个区域上分Ⅲ别使用积分公式Ox情况三：若积分区域D既不是x型区域又不是y型区域,⎛⎞则∫∫f(x,yd)σ=⎜∫∫+∫∫+∫∫⎟f(x,yd)σ.⎜⎟D⎝D1D2D3⎠\n典型例题例2改变积分212x−x22−x∫0dx∫0f(x,yd)y+∫1dx∫0f(x,yd)y的次序.解积分区域如图y=2−x2Y−型积分区域为y=2x−x21−1−y≤x≤2−y,0≤y≤.112−y原式=dyf(x,yd)x.∫∫201−1−y\n2例4计算∫∫xydσ,其中D是由抛物线y=x及Dy=x−2所围成的闭区域.32y+22解xydσ=[xydxd]y∫∫∫∫2−1y1D22xy+212345=∫[y]y2dy-1−12-21225=∫[y(y+)2−yd]y2−12461⎡y432y⎤5=⎢+y+2y−⎥=5.2⎣436⎦−18\n22−y例5求∫∫xedxdy,其中D是以0,0(),1,1(),)1,0(为D顶点的三角形区域.2−y解注意到∫edy无法用初等函数表示,所以积分时必须考虑次序.21y22−y2−y∫∫xedxdy=∫dy∫xedx00D321−y2y1−y2y212=∫e⋅dy=∫e⋅dy=1(−).03066e\n五、利用对称性简化二重积分的计算使用对称性时应注意：1.积分区域关于坐标轴的对称性；2.被积函数在积分区域上关于两个坐标变量的奇偶性.只有当积分区域和被积函数的对称性相匹配时,才能简化.\n二重积分计算的简化设f(x,y)∈C(D),计算I=∫∫f(x,yd)xdy.D.1D关于y轴对称.)1(f(−x,y)=−f(x,y),即f(x,y)关于x是奇函数时,I=.0)2(f(−x,y)=f(x,y),即f(x,y)关于x是偶函数时,I=2f(x,yd)xdy,D={(x,y)∈Dx≥0}.∫∫1D1\n二重积分计算的简化设f(x,y)∈C(D),计算I=∫∫f(x,yd)xdy.D.2D关于x轴对称.)1(f(x,−y)=−f(x,y)时,I=.0)2(f(x,−y)=f(x,y)时,I=2f(x,yd)xdy,D={(x,y)∈Dy≥0}.∫∫2D2\n二重积分计算的简化设f(x,y)∈C(D),计算I=∫∫f(x,yd)xdy.D.3D关于原点对称.)1(f(−x,−y)=−f(x,y)时,I=.0)2(f(−x,−y)=f(x,y)时,I=2∫∫f(x,yd)xdy=2∫∫f(x,yd)xdy.D1D2\n2222max{bx,ay}例6计算I=∫∫edσ,D其中D=({x,y|)−a≤x≤a,−b≤y≤b}.解由于被积函数关于x,y均为偶函数,且积分区域D关于y轴,x轴均对称,2222max{bx,ay}故I=4∫∫edxdy,D′其中D′={(x,y0|)≤x≤a0,≤y≤b}\nb若记D={(x,y0|)≤x≤a0,≤y≤x},1aaD={(x,y0|)≤y≤b0,≤x≤y},y2bby=xba222222则在D1上,max{bx,ay}=bx,D2D2222221在D2上,max{bxa,y}=ay,Oax⎛⎞2222于是I=4⎜ebxdxdy+eaydxdy⎟⎜∫∫∫∫⎟⎝D1D2⎠\nbxb2x2aab2x2ba22而edxdybx∫∫=∫0dx∫0edy=∫xedxa0D11a2b2=e(−1),2ab22baybeaydxdyba2y2aa2y2∫∫=∫dy∫edx=∫yedyD00b021a2b2=e(−1),2ab4a2b2从而得I=e(−1).ab\n七、二重积分的极坐标计算公式极坐标系中的面积元素dσ=ρdρdθdxdy=ρdρdθ⎧x=ρcosθ⎨⎩y=ρsinθθ+dθ二重积分的变量从直角坐θρdθ标到极坐标的变换公式dρ∫∫f(x,yd)xdyOρρ+dρρD=∫∫f(ρcosθ,ρsinθ)ρdρdθD\n适用范围)1(积分区域D的边界曲线用极坐标方程表示比较简单,通常D为圆域、圆环或扇形区域时,可考虑用极坐标计算;)2(被积函数使用极坐标后函数表达式可以简化22并易于积分,通常当被积函数中含有x+y的因式时可以考虑使用极坐标计算.\n二重积分化为累次积分几种常见的情形ρ=ρ(θ)2ρ=ρ(θ)D2ρ=ρθ()1()Dρ=ρ1θββααOρOρ情况一：D:ρ(θ)≤ρ≤ρ(θ),α≤θ≤β.12（注：极点在积分区域外）∫∫f(ρcosθ,ρsinθ)ρdρdθDβρ2(θ)=∫∫dθf(ρcosθ,ρsinθ)ρdρ;αρ1(θ)\n二重积分化为二次积分几种常见的情形ρ=ρ(θ)DβαOρ情况二：D:0≤ρ≤ρ(θ),α≤θ≤β.（注：极点在积分区域边界上）∫∫f(ρcosθ,ρsinθ)ρdρdθDβρ(θ)=∫dθ∫f(ρcosθ,ρsinθ)ρdρ;α0\n二重积分化为二次积分几种常见的情形情况三：D0:≤ρ≤ρ(θ),Dρ=ρ(θ)0≤θ≤2π.（注：极点在积分区域内）Oρ∫∫f(ρcosθ,ρsinθ)ρdρdθD2πρ(θ)=∫dθ∫f(ρcosθ,ρsinθ)ρdρ;00以上各种情形,区域D的面积S=∫∫ρdρdθ.D\n典型例题22−x−y例7计算∫∫edxdy,其中D是中心在原点,半径D222为a的圆域x+y≤a.解D0:≤ρ≤a,0≤θ≤2π.222πa2−x−y−ρ∫∫edxdy=∫dθ∫eρdρ00D2−a=π1(−e).\n222222例8计算∫∫(x+yd)xdy,D:x+y=2y,x+yD=4y,x−3y=,0y−3x=0所围成的平面区域.解边界曲线的极坐标方程22x+y=2y⇒ρ=2sinθ22x+y=4y⇒ρ=4sinθπx−3y=0⇒θ=6πy−3x=0⇒θ=3π(x2+y2d)xdy=34sinθ2⋅=π∫∫∫πdθ∫ρρdρ15(−3).2sinθ2D6\n22sin(πx+y)22例9求∫∫22dxdy,D1:≤x+y≤.4x+yD解积分区域关于坐标轴对称,被积函数关于坐标轴对称.22sin(πx+y)dxdy∫∫22D1x+yD22sin(πx+y)=4∫∫22dxdyx+yD1π2sinπρ2=4∫dθ∫ρdρ=−.401ρ\n九、三重积分的定义　　定义　设f(x,y,z)∈B(Ω),划分Ω为ΔΩ,?,ΔΩ,1nΔv表示ΔΩ的体积,对于∀(ξ,η,ζ)∈ΔΩ,作出乘积iiiiiinf(ξi,ηi,ζi)Δvi,并作和∑f(ξi,ηi,ζi)Δvi,记各小闭区i=1域直径中的最大值为λ,如果λ→0时和式的极限存在,则称极限值为f(x,y,z)在闭区域Ω上的三重积分,记作n∫∫∫f(x,y,zd)v=lim∑f(ξi,ηi,ζi)Δvi.λ→0Ωi=1\nn∫∫∫f(x,y,zd)v=lim∑f(ξi,ηi,ζi)Δvi.λ→0Ωi=1　　体积元素dv表示Δv,在直角坐标系下,三重积分i中的体积元素dv=dxdydz,从而三重积分记为∫∫∫f(x,y,zd)xdydz.Ω　　如果函数f(x,y,z)在闭区域Ω上连续,那么它在Ω上的三重积分必定存在.\n十、三重积分(tripleintegral)的物理意义　　如果f(x,y,z)表示某物体在点(x,y,z)处的体密度,Ω是该物体所占有的空间闭区域,f(x,y,z)在Ω上连续,n则∑f(ξi,ηi,ζi)Δvi是该物体质量M的近似值,当i=1λ→0时该和的极限就是该物体的质量M,即M=∫∫∫f(x,y,zd)v.Ω\n十一、三重积分的性质（三重积分与二重积分有类似的性质）性质１当k为常数时，∫∫∫kf(x,y,zd)v=k∫∫∫f(x,y,zd)v.ΩΩ性质２∫∫∫[f(x,y,z)±g(x,y,z)]dvΩ=∫∫∫f(x,y,zd)v±∫∫∫g(x,y,zd)v.ΩΩ\n性质３对区域具有可加性(Ω=Ω1+Ω2)∫∫∫f(x,y,zd)v=∫∫∫f(x,y,zd)v+∫∫∫f(x,y,zd)v.ΩΩ1Ω2性质４如果V是Ω的体积,则V=∫∫∫1⋅dv.Ω性质５如果在Ω上,f(x,y,z)≤g(x,y,z),则有∫∫∫f(x,y,zd)v≤∫∫∫g(x,y,zd)v.ΩΩ特殊地∫∫∫f(x,y,zd)v≤∫∫∫f(x,y,zd)v.ΩΩ\n性质６设m、M是函数f(x,y,z)在Ω上的最大值和最小值,V为Ω的体积,则在Ω上mV≤∫∫∫f(x,y,zd)v≤MV.Ω（三重积分估值不等式）性质７如果函数f(x,y,z)在Ω上连续,V为Ω的体积,则在Ω上至少存在一点(ξ,η,ς),使得∫∫∫f(x,y,zd)v=f(ξ,η,ς)⋅V.Ω（三重积分中值定理）\n三重积分在直角坐标系下的计算一、坐标面投影法二、坐标轴投影法(截面法)三、利用对称性简化三重积分的计算\n十二、坐标面投影法将积分区域Ω向xOy平面投影,得投影区域D.xyΩ={(x,y,z)z(x,y)≤z≤z(x,y(,)x,y)∈D}12xyzΣ2:z=z2(x,y)z(x,y),z(x,y)∈C(D).12xyΩ:xy型空间区域Ω特点:任何一条垂直于xOy面且穿过Ω内部的Σ:z=z(x,y)11直线与Ω的边界曲面ΣOy相交不多于两点.Dxxy\nzΣ2:z=z2(x,y)z2Ωz1Σ:z=z(x,y)11OyD(x,y)xxy当函数f(x,y,z)在Ω上连续时z2(x,y)∫∫∫f(x,y,zd)v=∫∫∫(f(x,y,zd)zd)xdyz1(x,y)ΩDxy叠积分\nΩ:yz型空间区域xΣ:x=x(y,z)22x2Ωx1Σ:x=x(y,z)11OzD(y,z)yyzx2(y,z)∫∫∫f(x,y,zd)v=∫∫∫(f(x,y,zd)xd)ydzx1(y,z)ΩDyz\nΩ:zx型空间区域yΣ:y=y(z,x)22y2Ωy1Σ:y=y(z,x)11OxD(z,x)zzxy2(z,x)∫∫∫f(x,y,zd)v=∫∫∫(f(x,y,zd)yd)zdxy1(z,x)ΩDzx\n例11计算三重积分∫∫∫xdxdydz,其中Ω为三个坐标Ω面及平面x+2y+z=1所围成的闭区域.z解作闭区域Ω如图所示.C)1,0,0(将Ω投影到xOy面上,得投影区域Dxy,1B,0()0,2D为三角形闭区域OAB.OyxyDxyA)0,0,1(边界方程依次为y=,0x=,0xx+2y=,11−x所以D={(x,y0|)≤y≤,0≤x≤1}.xy2\n在Dxy内任取一点(x,y),过此点作平行于z轴的直线,该直线通过平面z=0穿入Ω内,然后通过平面z=1−x−2y穿出Ω外.1−x11−x−2y∫∫∫xdxdydz=∫dx∫∫2dyxdz000Ω1−x1=∫xdx∫21(−x−2yd)y0011231=∫(x−2x+xd)x=.4048\n十三、坐标轴投影法(截面法)　　将空间区域Ω向z轴投影,z得到投影区间[p,q].qΩ(:x,y)∈D,p≤z≤q.zΩ:z型空间区域.zD特点:当p)0所围成.z解由对称性知∫∫∫xdv=,0∫∫∫ydv=,0ΩΩHD32222且∫∫∫zdv=2∫∫∫zdv,z=x+y−1ΩΩ1D2ODy1x222x+y=1+H其中Ω为Ω的位于xoy面上方的部分,它由平面z=122,0z=H和双曲面z=x+y−1所围成.\n方法：用先重后单的积分次序222Ω：{(,,)xyzx|+≤+≤≤y1,zz0H}1H22∫∫∫zdv=∫0dz∫∫zdxdyΩ1DzH22=∫z⋅π1(+zd)z032πH⎛3H⎞=⎜⎜1+⎟⎟.3⎝5⎠\n三重积分在柱坐标系下的计算一、柱面坐标系下的计算二、球面坐标系下的计算\n十五、柱面坐标系　　设M(x,y,z)为空间内一点,并设点M在xOy面上的投影P的极坐标为ρ,θ,则这样的三个数ρ,θ,z就叫点M的柱面坐标.z规定ρ,θ,z的变化范围为M(x,y,z)0≤ρ<+∞,0≤θ≤2π,−∞