初中二次函数总复习课件 31页

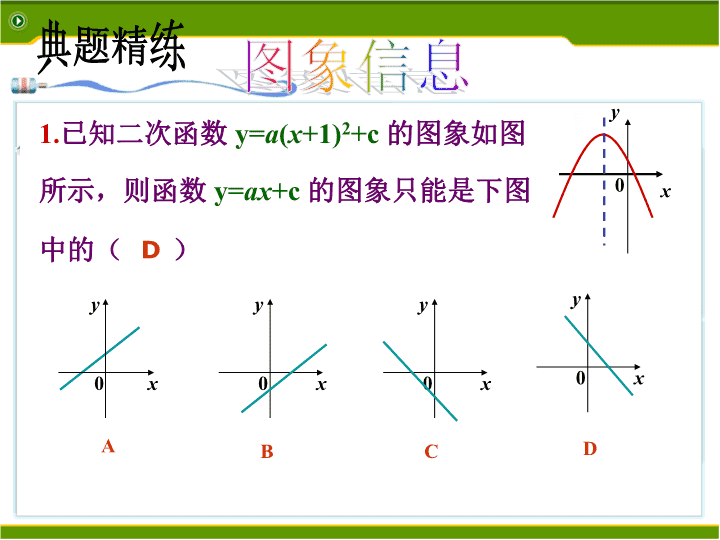
小恒山中学张秀坤二次函数复习课xOyxyO\n二次函数知识导航：1、二次函数的定义2、二次函数的图像及性质3、求解析式的三种方法4、二次函数的图象与系数之间的关系5、抛物线的平移6、二次函数与一元二次方程的关系7、二次函数的综合应用\n典题精练图象信息1.已知二次函数y=a(x+1)2+c的图象如图所示，则函数y=ax+c的图象只能是下图中的（）x0yAx0yBCx0yDx0y0xyD\n典题精练2.在同一坐标系中，一次函数y=ax+b和二次函数y=ax2+bx的图形可能是（）x0yAx0yBx0yCxy0DA图象信息小结：双图象的问题，寻找自相矛盾的地方。即由一个图象得出字母的取值范围，再去检验这个字母的符号是否适合另一个图象.\n3.如图,抛物线y=ax2+bx+c,请判断下列各式的符号：①a____0;②c____0;③b2-4ac____0;④b___0;典题精练图象信息＜xyO＞＞＞\nxyO变式1：若抛物线的图象如图，则a=.典题精练图象信息-1由a2-1=0，得a=±1\nxyO变式2：若抛物线的图象如图，则△ABC的面积是。ABC典题精练图象信息3由x2-4x+3=0,得x1=1,x2=3,∴AB=2.\n用待定系数法求解析式典题精练根据下列条件，求关于x的二次函数的解析式：（1）抛物线经过点（-1，11），（2，8），（0，6）三点；（2）抛物线经过点（0，1），（-1，0），（1，0）三点；（3）抛物线的顶点坐标是（3，-1），且经过点（2，3）.设y=ax2+bx+c，把以上三点代入求解；设y=a(x+1)(x－1),把点（0，1）代入求解或同（1）；设y=a(x-3)2-1,把（2，3）代入求解.\n典题精练二次函数y=ax2+bx+c(a≠0)的图象如图所示，根据图象解答下列问题：(1)写出方程ax2+bx+c=0的两个根；(2)写出不等式ax2+bx+c＞0的解集；3x123-112-1-2y0x1=1,x2=31＜x＜3用函数观点看一元二次方程\n典题精练二次函数y=ax2+bx+c(a≠0)的图象如图所示，根据图象解答下列问题：3x123-112-1-2y0(4)若方程ax2+bx+c=k有两个不相等的实数根，求k的取值范围.(3)写出y随x的增大而减小的自变量x的取值范围；x＞2k＜2用函数观点看一元二次方程\n2、在我市开展的创文明小区活动中，某居民小区要在一块一边靠墙（墙长为15m）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成（如图所示）.若设花园的BC边长为x(m),花园的面积为y(m2).典题精练最值问题DABC（1）求y与x之间的函数关系式，并写出自变量x的取值范围；∴y=解:(1)根据题意得：y=x(40-x),\n2、在我市开展的创文明小区活动中，某居民小区要在一块一边靠墙（墙长为15m）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成（如图所示）.若设花园的BC边长为x(m),花园的面积为y(m2)。典题精练最值问题（2）根据（1）中求得的函数关系式，判断当x取何值时，花园的面积最大？最大面积为多少？对称轴是x=20.∴当0＜x≤15时，y随x的增大而增大，∴当x=15时，y有最大值，y最大值=即：当x=15时，花园面积最大，最大面积为187.5m2解:y=的图像是开口向下的抛物线，15187.50xy20\n典题精练拱桥与水位问题如图，河上有一座抛物线桥洞，已知桥下的水面离桥拱顶部3m时，水面宽AB为6m.(1)当水位上升0.5m时，求水面的宽度CD为多少米？3x123-312-1-2y0BCADE解：设此抛物线的解析式为y=ax2+c，由题意知过点（0，3），（3，0）,代入解析式解得:a=-,c=3,所以抛物线的解析为：y=-x2+3.把y=0.5代入上述解析式，得x=则CD=m.31\n典题精练拱桥与水位问题3x123-312-1-2y0BAE(2)有一艘游船，它的左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在上述河流中航行.若游船宽为2m，从水面到棚顶的高度为1.8m，问这艘游船能否从桥洞下通过？解：当y=1.8m时，代入y=x2+3,解得x=,这时桥洞的宽度为，而＞2，所以这艘船能人桥洞下通过.如图，河上有一座抛物线桥洞，已知桥下的水面离桥拱顶部3m时，水面宽AB为6m.\n典题精练拱桥与水位问题3x123-312-1-2y0BAE(2)有一艘游船，它的左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在上述河流中航行.若游船宽为2m，从水面到棚顶的高度为1.8m，问这艘游船能否从桥洞下通过？解：当x=1时，代入y=x2+3,得y=,这时桥洞的高度为米，而＞1.8，所以，此船能从桥洞下通过.如图，河上有一座抛物线桥洞，已知桥下的水面离桥拱顶部3m时，水面宽AB为6m.\n(连云港)丁丁推铅球的出手高度为1.6m,在如图所示的直角坐标系中，铅球的运行路线近似为抛物线①求k的值；聚焦中考xyO典题精练(0,1.6)解：由图像可知，抛物线过点(0,1.6)即当x=0时，y=1.61.6=-0.1k2+2.5k=±3又因为对称轴是在y轴的右侧，即x=k>0所以，k=3B3\n(连云港)丁丁推铅球的出手高度为1.6m,在如图所示的直角坐标系中，铅球的运行路线近似为抛物线(0,1.6)聚焦中考xyO典题精练②求铅球的落点与丁丁的距离;解：由-0.1(x-3)2+2.5=0，解之得，x1=8,x2=-2，所以，OB=8.故铅球的落点与丁丁的距离是8米。B\n(连云港)丁丁推铅球的出手高度为1.6m,在如图所示的直角坐标系中，铅球的运行路线近似为抛物线(0,1.6)③一个1.5m的小朋友跑到离原点6米的地方(如图)，他会受到伤害吗？聚焦中考xyO典题精练B解：当x=6时，y=-0.1(6-3)2+2.5=1.61.6＞1.5所以，这个小朋友不会受到伤害.\n感悟与反思：谈谈这堂课有什么收获吧！\n1.数形结合是本章主要的数学思想，通过画图将二次函数直观表示出来，根据函数图象，就能知道函数的开口方向、顶点坐标、对称轴、变化趋势、与坐标轴的交点、函数的最值等问题。2.待定系数法是本章重要的解题方法，要能通过三个条件确定二次函数的关系式；灵活根据题中的条件，设出适合的关系式。3.建模思想在本章有重要的应用，将实际问题通过设自变量，建立函数关系，转化为二次函数问题，再利用二次函数的性质解决问题。总结提升\n教师寄语：A代表成功，x代表艰苦的劳动，y代表正确的方法，z代表少说空话。A=x+y+z-------爱因斯坦\n再见！xOy0xyxyo\n形如y=ax²＋bx＋c（a、b、c是常数，a≠0）的函数，叫做二次函数.定义要点：①a≠0;②最高次数为2;③代数式一定是整式.1、二次函数的定义\n抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定a>0,开口向上a<0,开口向下在对称轴的左侧,y随着x的增大而减小；在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大；在对称轴的右侧,y随着x的增大而减小.xy0xy02、二次函数的图像及性质直线直线\n⑵顶点式：已知抛物线顶点坐标（h,k），通常设抛物线解析式为___________________.⑶交点式:已知抛物线与x轴的两个交点(x1,0)、(x2,0),通常设解析式为______________________.⑴一般式：已知抛物线上的三点，通常设解析式为______________y=ax2+bx+c(a≠0).y=a(x-h)2+k(a≠0).y=a(x-x1)(x-x2)(a≠0)3、求抛物线解析式的三种方法\n顶点式的特殊情况：y=ax2(a≠0)顶点在y轴上y=ax2+c(a≠0)顶点在x轴上y=a(x-h)2(a≠0)顶点是原点顶点位置图象(a＞0)解析式模式\n4、抛物线y=ax2+bx+c的符号问题：（1）a的符号：由抛物线的开口方向确定开口向上a>0开口向下a<0（2）c的符号：由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0交点经过原点c=0\n（3）b的符号：由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0（4）b2-4ac的符号：由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0左同右异\n（5）a+b+c的符号：因为x=1时,y=a+b+c,所以a+b+c的符号由x=1时，对应的y值决定。当x=1时，y>0,则a+b+c>0；当x=1时，y<0，则a+b+c<0；当x=1时，y=0，则a+b+c=0.（6）a-b+c的符号：因为x=-1时,y=a-b+c,所以a-b+c的符号由x=-1时，对应的y值决定。当x=-1，y>0,则a-b+c>0；当x=-1，y<0,则a-b+c<0；当x=-1，y=0,则a-b+c=0.\n(左加右减，上加下减)略显身手：⑴二次函数y=2x2的图象向平移个单位可得到y=2x2-3的图象；⑵二次函数y=2x2的图象向平移个单位可得到y=2(x-3)2的图象。⑶二次函数y=2x2的图象先向平移个单位，再向平移个单位可得到函数y=2(x+1)2+2的图象。下3右3左1上2延伸：y=2(x+3)2-4y=2(x+1)2+25、抛物线的平移\n判别式：b2-4ac二次函数y=ax2+bx+c图象(a＞0)一元二次方程ax2+bx+c=0（a＞0）的根有两个不相等的实数根b2-4ac＞0xyO有两个相等的实数根b2-4ac=0xOyxyO没有实数根b2-4ac＜06、二次函数与一元二次方程的关系