算法导论复习资料 17页

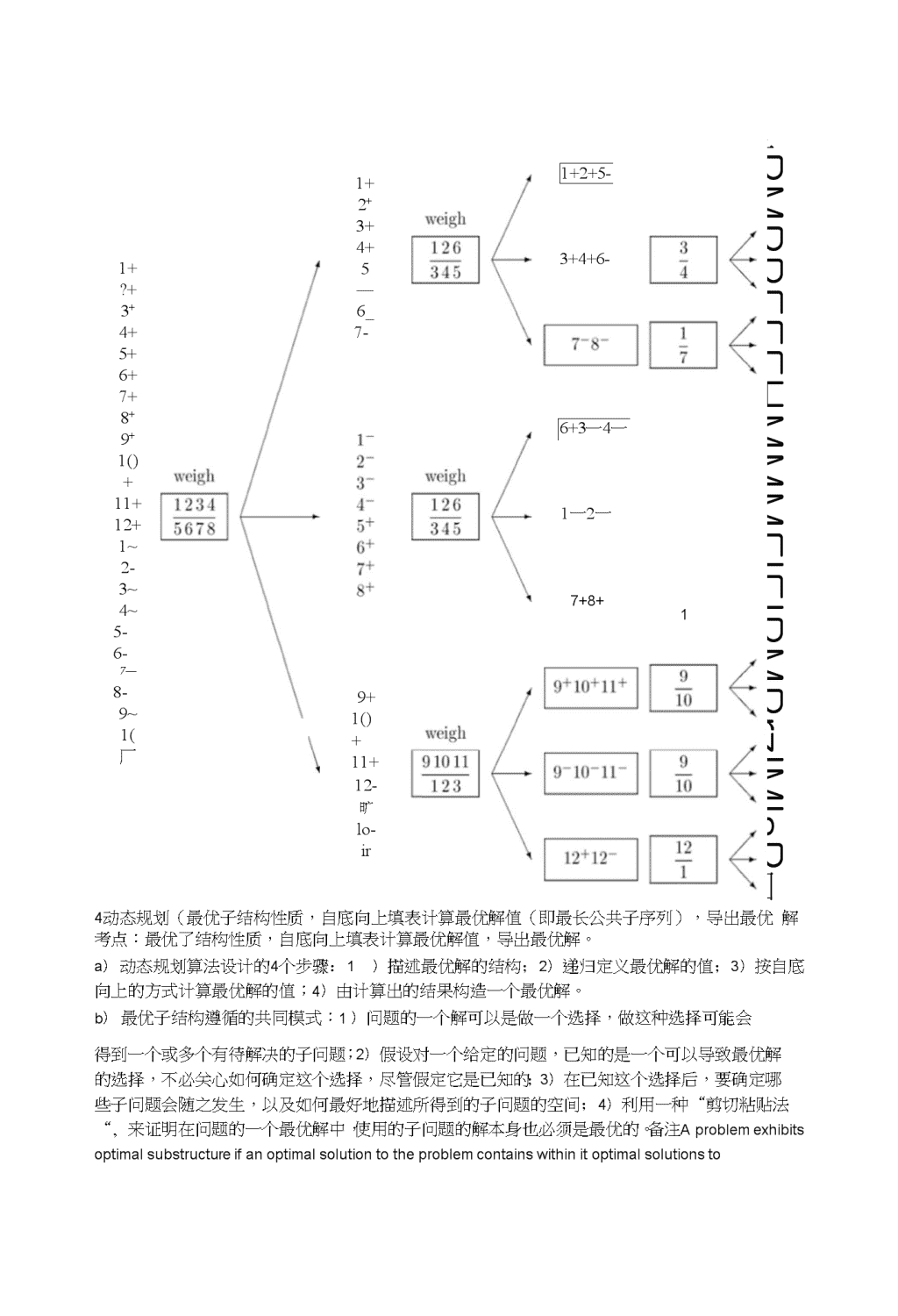
算法导论复习资料一、选择题：第一章的概念、术语。二、考点分析：1、复杂度的渐进表示，复杂度分析。2、正确性证明。考点：1)正确性分析(冒泡，归并，选择)；2)复杂度分析(渐进表示O,Q,©,替换法证明，先猜想，然后给出递归方程)。循环不变性的三个性质：1)初始化：它在循环的第一轮迭代开始之前，应该是正确的；2)保持：如果在循环的某一次迭代开始之前它是正确的，那么，在下一次迭代开始之前，它也应该保持正确；3)当循环结束时，不变式给了我们一个有用的性质，它有助于表明算法是正确的。插入排序算法：INSERTION-SORT(A)1forj<-2tolength[A]2dokey<-A[j]3>InsertA[j]intothesortedsequenceA[1,j-1].4i<-j-15whilei>0andA[i]>key6doA[i+1]<-A[i]7i<-i-18A[i+1]<-key插入排序的正确性证明：课本11页。归并排序算法：课本17页及19页。归并排序的正确性分析：课本20页。3、分治法(基本步骤，复杂度分析)。一一许多问题都可以递归求解考点：快速排序，归并排序，渐进排序，例如：12球里面有一个坏球，怎样用最少的次数找出來。(解：共有24种状态，至少称重3次可以找出不同的球)不是考点：线性时间选择，最接近点对，斯特拉算法求解。解：基本步骤：一、分解：将原问题分解成一系列的子问题；二、解决：递归地解各子问题。若子问题足够小，则直接求解；三、合并：将子问题的结果合并成原问题的解。复杂度分析：分分治算法中的递归式是基于基本模式中的三个步骤的，T(n)为一个规模为n的运行时间，得到递归式T(n)=Q(1)n<=cT(n)=aT(n/b)+D(n)+C(n)n>c附加习题：请给出一个运行时间为Q(nlgn)的算法，使之能在给定的一个由n个整数构成的集合S和另一个整数x时，判断出S中是否存在有两个其和等于x的元素。\nGivea0(nlgn)timealgorithmfordeterminingifthereexisttwoelementsinansetSwhosesumisexactlysomevaluex.Algorithm4CheckSums(A.x)Input:AnanayAandavaluex.Output:AbooleanvalueindicatingifthereistwoelementsinAwhosesumisx.A<—SORT(A)n<—/engt/i[A]foritottdoifA[i]>0andBinary・Search(A,A|i]一xj.n)thenreturntrueendifendforreturnfalseClearlythisalgorithmdoesthejob.(Itisassumedthatnilcannotbetmeintheif-statement.)\n1+?+3+4+5+6+7+8+9+1()+11+12+1~2-3~4~5-6-7—8-9~1(厂11-12-1+2+3+4+5—6_7-8-9+1()+11+12-旷lo-ir12-3+4+6-1一2一5+1+2+5-6+3一4一7+8+1叵RMRREEEHMMMElEIRMRrzlMlsR回一3EMSH4动态规划（最优子结构性质，自底向上填表计算最优解值（即最长公共子序列），导出最优解考点：最优了结构性质，自底向上填表计算最优解值，导岀最优解。a）动态规划算法设计的4个步骤：1）描述最优解的结构；2）递归定义最优解的值；3）按自底向上的方式计算最优解的值；4）由计算出的结果构造一个最优解。b）最优子结构遵循的共同模式：1）问题的一个解可以是做一个选择，做这种选择可能会得到一个或多个有待解决的子问题；2）假设对一个给定的问题，已知的是一个可以导致最优解的选择，不必关心如何确定这个选择，尽管假定它是已知的；3）在已知这个选择后，要确定哪些子问题会随之发生，以及如何最好地描述所得到的子问题的空间；4）利用一种“剪切粘贴法“,来证明在问题的一个最优解中，使用的子问题的解本身也必须是最优的。备注Aproblemexhibitsoptimalsubstructureifanoptimalsolutiontotheproblemcontainswithinitoptimalsolutionsto\nsubproblems.Wheneveraproblemexhibitsoptimalsubstuctureitisagoodcluethatdynamicprogrammingmightapply.c)最长公共子序列的算法：这里以两个序列X二｛x1,x2，…,xm｝和Y二｛屮旳…如｝为输入，注意课本211页的自底向上填表方法。LCS-LENGTH(X,Y)注：此程序运行时间为0(mn),每个表项的计算时间为0(1)Im<-lengthp(]2n■length[Y]3fori<-1tom4doc[ir0]<-05forjOton6doc[0,j]«07fori<-1tom8doforj<-1ton9doifxi=yj10thenc[irj]<-c[i-1J-1]+1IIb[i,j]<-t4="12elseifc[i-1J]>(:[i,j・1]13thenc[ifj]jc[i-1,j]14b[i,j]〜7”15elsec[ij]<-c[i,j-1]16b[i,j]〜””17returncandbPRINT・LCS(b,X,i,j)注：此程序运行时间为0(m+n)1ifi=Oorj=02thenreturn3ifb[i,j]=n=n4thenPRINT-LCS(b,X,i-1rj-1)5printxi6elseifb[i,j]=T”7thenPRINT-LCS(b,Xfi-1rj)8elsePRINT・LCS(bX,i,j・1)d)矩阵链乘法的算法：参照课本上的矩阵链表得出矩阵相乘的最小算法。\nva\x\｛m[i.k]+m[k+1J]ilisthechainlength.5dofori<-1ton-1+16doj<-i+1-17m[i,j]■88fork<-itoj-19doq<-m[i,k]+m[k+1,j]+pi-1pkpj10ifqFindthefirstactivityinSij.\n1dom<-m+12ifm0,wt>0.vt>0,且分别对畔％进行排序后有聊<聊+「号+1，1VX/7・1,要求找一个力元向量(X\,X"…，xj,x£(0,1丿，1=temp)&&(iP(x“2,…,“)0/T称G为流网络。流的定义：流网络G,若函数卩：l/X1/tF满足下述条件：-容量限制：对任意(qu)eF,有0<=p(u/v)<=c(u,v)-守恒条件：对任意uw(V・{s,t}),有艺一22/?(V,7/)=0则称p为G上的流。注意课本399页的引理。2)对源点顶点来说，离开它的正流要比进入它的正流更多；对汇点顶点来说，进入它的正流要比离开它的正流更多。先证明如下：|f|=f(s,V)=f(V,V)・f(V・s,V)=f(V,V-s)=f(V,t)+f(V,V-s-t)=f(V,t)3)Ford-Fulkerson方法：此方法依赖三中重要思想，比残留网络;b、增广路径;c、割。这些是最大流最小割定理的精髓。(Ford-Fulkerson方法沿增广路径反复增加流，知道找出最大流为止；而最大流最小割定理告诉我们：一个流是最大流，当且仅当它的残留网络不包含增广路径。)一、残留网络：在不超过容量c(u,v)的条件下，从u到v之间可以压入的额外网络流量，就是(u,v)残留容量，定义为&(u,v)=c(u,v)-f(u,vX注意课本401页的残留网络的例子。残留网络Gf本身也是一个流网络，其容量由Cf给出，且|Ef|<=2|E|o注意课本402页的引理\n二、增广路径：注意课本403页引理263和引理26.4。\n三、流网络的割：注意403页的几个引理。四、最大流最小割定理：几个相互等价的条件。FORD・FULKERSON(G,s,t)1foreachedge(u,v)wE[G]2dof[u,v]<-03f[v,u]<-04whilethereexistsapathpfromstotintheresidualnetworkGf5docf(p)<-min{cf(uzv):(u,v)isinp}6foreachedge(u,v)inp7dof[u,v]<-f[u,v]+cf(p)8f[v,u]<--f[u,v]FORD-FULKERSON的复杂性：FORD-FULKERSON过程的运行时间取决于如何决定第四行中的增广路径，选择不好，算法可能不会终止。假设容量是整数•1〜3行0(|E|)•4〜8循环执行0(|f*|)•找增广路0(|E|)•O(|E||f*|)FORD-FULKERSON算法有其缺点，可以参照课本406页。2)Edmonds-Karp算法：如果在第四行中用广度优先搜索来实现对增光路径p的计算。即如果增光路径是残留网络中从s到t的最短路径(其中每条边为单位距离，或权)，则能够改进FORD-FULKERSON算法的界；称FORD-FULKERSON方法的这种实现为Edmonds-Karp算法。Edmonds-Karpg法的运行时间为0(V*E2)注意课本407页关于Edmonds-Karpg法的一些证明。8、NP完全问题(多项式时间规约)。考点：多项式时间内的规约问题，掌握NP完全问题的证明方法。P类问题：是在多项式时间内可解的问题，即都是在0(卅)时间内求解的问题，此处k为某个常数，n是问题的输入规模。NP类问题：是在多项式时间内"可验证"的问题即能够在问题输入规模的多项式时间内，验证该问题是正确的。注意：P问题包含于NP问题。但P不一定是NP问题的真子集。NPC问题：NP完全问题，即任何一个NP问题都能通过一个多项式时间算法转换为某个NP问题，那么这个NP问题就成为NPC问题。换言之，如果这个问题解决了，那么所有的NP问题也都能解决了。若问题L满足-LwNP,and-L‘^PLforeveryL'eNP.则问题L是NPC的,若L只满足条件2则称问题是NP・hard的。\n注意：如果任何NP完全问题可以在多项式时间内解决，则NP中所有问题都有一个多项式时间的算法。\n1）多项式时间内的规约：-若问题2可以被多项式时间求解，则问题1也可被多项式时间求解；-若问题1不能被多项式时间求解，则问题2也不能多项式时间求解；-problem1wpproblem2表明：问题1的求解不"难"于问题厶假定一个判定问题A和另外一个不同的判定问题B,在一个过程中，它能将A的任何势力苗专换为B的、具有以下特征的势力b：a.转化操作需要多项式时间；b、两个实例的答案是相同的，即a的答案是〃是"，当且仅当b的答案也是〃是"，称这样的过程为多项式时间的规约算法。可以参照课本599页的图。&给定问题A的一个实例a,利用多项式时间规约算法，将它转换为问题B的一个实例b。b、在实例b上，运行B的多项式时间判定算法。c、将b的答案用作a的答案。可以将对问题A的求解〃规约"为对问题B的求解。注意：第一个NP完全问题就是电路可满足性问题。2）NP完全性与可归约性：课本609页引理34.33）电路可满足性问题：引理：电路可满足性问题属于NP类、NP难度及NP完全的。例题解析：1、设有一个长度为N的数字串，要求选手使用K个乘号将它分成K+1个部分，找出一种分法，使得这K+1个部分的乘积能够为最大。（EX：有一个数字串：312,当N=3,K=1时会有以下两种分法：3*12=36、31*2=62,这时，符合题目要求的结果是：31*2=62。）2、Olay教授是一家石油公司的顾问，这家公司正在计划建造一条由东向西的大型管道，它穿过一个有n口油井的油田。从每口井中都有一条喷油管道沿最短路径与主管道直接连接（或南或北）。给定各口井的x坐标和y坐标，应如何选择主管道的最优位置（使得各喷管长度总和最小）？证明最优位置可在线性时间内确定。3、NPC证明：如集合的等划分问题，TSP问题，最小顶点覆盖问题。一、证明：顶点覆盖问题是NP完全问题。将3SAT变换到VC.设U={u1/u2,...,un},C={c1,c2,..,cm}是3SAT的实例.如下构造图G,分量设计法.真值安排分量：Ti=（Vi,EiX1就是TSP的一个实例，它很容易在多项式时间内产生。现在说明图G中具有一个汉密尔顿回路，当且仅当图&中有一个费用至多为0的回路。假定图G中有一个汉密尔顿回路h,h中的每条边度属于E,因此在&中的费用为0。因此h在&中的费用为0的回路。反之，假定图&中有一个费用JY至多为0的回路。由于E，中边的费用只能是0或1,故回路h，的费用就是0,且回路上每条边的费用必为0。故IY仅包含E中的边。三、证明：集合的等划分问题是NP完全问题。实例：有穷集ArVaeA,s(a)eZ+.问：是否存在A，cA,使得》£(a)=工只。)显然均分是NP类问题。下面将§DM变攬龊j分问题设W,X,Y,MuWxXxY是3DM的实例，其中|W|=|X|=|Y|=q,W={w1,w2—,wq}X={x1rx2r...,xq}Y={y1,y2,.・.，yq}M=,mk}构造A,|A|二k+2对应于每个mi=(wf(i),xg(i),yh(i))Wai.s(ai)为二进制数，分成3q段，每段有p=「log(k+1)1位，共计3pqlog(k+1),2p>k+1,k<2p-1r当k个1相加时不会产生段之间的进位3q—1B=£2刃=2"(列7+2"创一2)+…+2?"+2"+2°戶oB的段数与s(ai)—样，每段的最右位为1,其它为0例如：W={w1fw2}rX={x1rx2}rY={yty2}rM={(w1,x2,y2),(w1,x2,y1),(w2,x1,y1)}p=riog(3+1)1=2元素a1,a2,a3分别对应(w1,x2,y2),(w1,x2,y1),(w2,x1,y1)s(a1)=010000010001=210+24+20s(a2)=010000010100=210+24+22s(a3)=000101000100=28+26+22B=010101010101子集A，={ai:1(a)<=1aeA—A9证明题的考点：1、正确性证明问题。2、替换法证明问题。3、贪心选择性质证明问题。4、NP完全问题的证明。5、最大流问题的证明。简单题的考点：1、回溯法基本思想和步骤。2、分治算法的基本方法和步骤。3、搜索算法的基本方法和步骤。4、动态规划问题的基木方法和步骤。5、分支界限算法的基本方法和步骤。