高中课件合情推理 25页

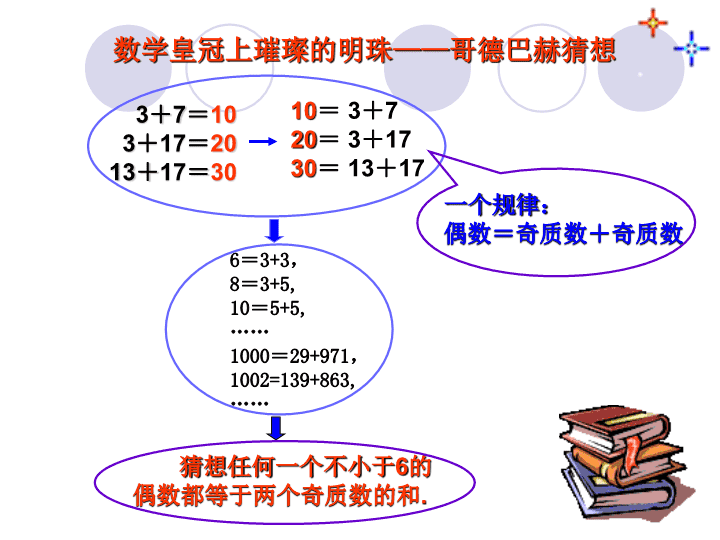
合情推理\n已知的判断新的判断确定根据一个或几个已知的判断来确定一个新的判断的思维过程就叫推理.\n3＋7＝103＋17＝2013＋17＝3010＝3＋720＝3＋1730＝13＋176＝3+3，8＝3+5,10＝5+5,……1000＝29+971，1002=139+863,……猜想任何一个不小于6的偶数都等于两个奇质数的和.数学皇冠上璀璨的明珠——哥德巴赫猜想一个规律：偶数＝奇质数＋奇质数\n哥德巴赫猜想的过程：具体的材料观察分析猜想出一般性的结论归纳推理的过程：\n由某类事物的具有某些特征,推出该类事物的都具有这些特征的推理,或者由概括出的推理,称为归纳推理(简称归纳).部分对象全部对象个别事实一般结论归纳推理简言之，归纳推理就是从部分到整体,从个别到一般的推理.\n1，3，5，7，…，由此你猜想出第个数是_______.你想起来了吗？\n例题1观察下列的等式,你有什么猜想吗?1+3=4=221+3+5=9=321+3+5+7=16=421+3+5+7+9=25=52……由此猜想:前n个连续的正奇数的和等于n的平方,即:1+3+5+…+(2n-1)=n2\n练习：30页第1，2题\n\n\n欧拉的旅程观察上表，请你猜想多面体的F、V、E有什么关系？F+V-E=2\n归纳推理的过程\n枚举归纳法\n因果归纳法共分为\n传说在古老的印度有一座神庙，神庙中有三根针和套在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规则,把圆环从一根针上全部移到另一根针上，第三根针起“过渡”的作用.1.每次只能移动1个圆环；2.较大的圆环不能放在较小的圆环上面.如果有一天，僧侣们将这64个圆环全部移到另一根针上，那么世界末日就来临了.请你试着推测：把个圆环从1号针移到3号针,最少需要移动多少次?123游戏：河内塔（TowerofHanoi）\n123第1个圆环从1到3.设为把个圆环从1号针移到3号针的最少次数，则＝1时，＝1\n＝2时，123第1个圆环从1到3.前1个圆环从1到2;第2个圆环从1到3;第1个圆环从2到3.设为把个圆环从1号针移到3号针的最少次数，则＝1＝1时，＝3\n＝2时，＝3＝1时，＝1＝3时，123第1个圆环从1到3.前1个圆环从1到2;第2个圆环从1到3;前1个圆环从2到3.前2个圆环从1到2;第3个圆环从1到3;前2个圆环从2到3.设为把个圆环从1号针移到3号针的最少次数，则＝7\n思考：n=4时，我们得到依次移动1,2,3,4个圆环所需最少次数构成数列1,3,7,15观察这个数列，可以发现其中蕴含如下规律：由此猜想：移动n个圆环最少需要移动次数为\n由平面内的圆，我们联想到空间里的球，让他们来类比．你能找到他们有哪些类似的特征？请同学们完成课本25页的探究．补充：圆有切线，而球有切平面\n这种由两类对象具有某些类似特征和其中一类对象的某些特征推出另一类对象也具有这些特征的推理称为类比推理．类比推理是由特殊到特殊的推理．思考？类比实数中的加法与乘法，他们有哪些类似的性质？\n我们要根据实际情况选择适当的类比对象．如：平　面空　间正方形正方体圆球三角形三棱锥\n例题４：类比平面内直角三角形的勾股定理，试给出空间中四面体性质的猜想练习：30页第3题cab\n归纳推理和类比推理都是根据已有的事实，经过观察、分析、比较、联想，再进行归纳、类比，然后提出猜想的推理，我们把它们统称为合情推理合情推理得出得的结论只是一种猜想，并不一定是正确的。如：费马猜想。\n小结：１.归纳推理和类比推理的概念２.能简单的运用合情推理作业：35页A组1-6