高中函数课件 39页

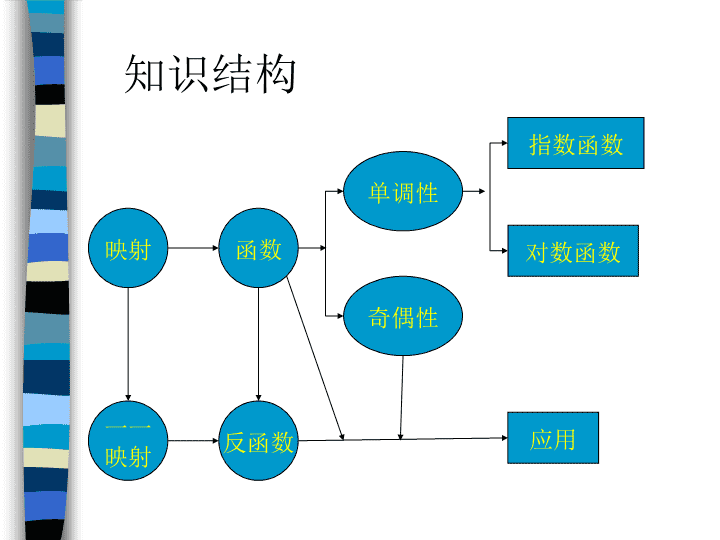
函数\n一一映射反函数映射函数奇偶性单调性应用对数函数指数函数知识结构\n（一）知识点归纳1、映射、函数、函数的三要素、函数的单调性、函数奇偶性。2、反函数，互为反函数的函数图像间的关系。3、指数,对数;指数函数,对数函数（二）典例分析（三）单元测试\n例1函数y=log(x2-2x+3)的定义域为_____值域为_____，单调增区间为______，减区间为______。解：x2-2x+3>0∴x∈Rx2-2x+3=(x-1)2+2≥2∴y=log(x2-2x+3)≤-1单调增区间为（-∞,1]，减区间为[1,+∞）\n例2y=log2的值域为_______，增区间为______，减区间为_______。解：-(x2-6x+5)>0x2-6x+5<010,且a≠1)解的个数为______。解：-x2+2x+2a=-(x-1)2+2a+12a+1>a+1AByx10xyx=120\n例10已知x1是方程x+lgx=4的解，x2是方程x+10x=4的解，则x1+x2=_____。（A）5（B）4（C）3（D）1法1：∵x1+lgx1=4又x2+10x2=4∴30，a≠1为常数，函数f(x)=loga（1）讨论f(x)在区间(-∞,-5)内的单调性，并给予证明。（2）设g(x)=1+loga(x-3)如果方程f(x)=g(x)有实根，求a的范围。解：设U(x)=x11时f(x)=loga在(-∞,-5)上是增函数。当00)a(t+2)=∴==t++12≥12+4∴a≤=∴00，且x1+x2<-2，则f(-x1)与f(-x2)的大小关系是（A）(A)f(-x1)>f(-x2)(B)f(-x1)=f(-x2)(C)f(-x1)03a2-2a+1>0∴2a2+a+1>3a2-2a+1a2-3a<001，变数x,y之间有关系式：logax+3logxa-logxy=3。（1）若x=at(t≠0)，试求以a,t表示y的表达式；（2）若t的变化范围为[1,+∞)此时y的最小值为8，求a和x值。解：（1）logax+3logxa-logxy=3∴=logax+-3∴logay=loga2x-3logax+3y=a=a（2）当t=时y小=a=8∴a=8=16此时x=16=64\n19）已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx，其中a,b,c满足a>b>c,a+b+c=0（1）求证：两函数的图像交于不同的两点A，B；（2）求线段AB在x轴上的射影A1B1的长的取值范围。解：(1)y=ax2+bx+c∴ax2+bx+c=-3xy=-bxax2+2bx+c=0①△=4b2-4ac=4(-a-c)2-4ac=4[(a+)2+c2]∵a>b>ca+b+c=0∴a>0c<0∴△>0∴两函数图象交于两个不同点。\n（2）设方程两个根分别为x1,x2则x1+x2=-x1x2=|A1B1|2=(x1+x2)2-4x1x2=(-)2-===4a>b>ca+b+c=0∴a>0c<0a>-a-c>c∈(-2,-)∴|A1B1|2∈(3,12)<|A1B1|<2\n20）如图所示，铁路线上AB段长100千米，工厂C到铁路的距离CA为20千米，现在要在AB上某一点D处，向C修一条公路，已知铁路与公路的每吨千米的运费之比为3:5，为了使原料从供应站B运到工厂C的运费最省。D点应选在何处？解：设|AD|=x铁路上每吨千米运费为3k，公路为5k。总运费y=5k+3k(100-x)(0≤x≤100)∴=5-3xADBC\n令=t∴(t+3x)2=25(x2+400)∴16x2-6tx+10000-t=0△=36t2-4×16(10000-t)≥0∴t≥80当t=80时x=15时，即D取在距A15千米处，总运费量省。法2设∠ACD=a则总运费量y=3(100-20tana)+5×=300+()小=此时tana=∴AD=15（千米）\n21）已知函数f(x)=3x且f-1(18)=a+2，g(x)=3ax-4x的定义域为区间[0,1]。（1）求g(x)的解析式；（2）求g(x)的单调区间，确定其增减性并试用定义证明；（3）求g(x)的值域。解：（1）∵f(x)=3x且f-1(18)=a+2∴f(a+2)=3a+2=183a=2∴g(x)=2x-4x\n（2）令t=2g(t)=t-t2=-(t-)2+t∈[1,2]∵g(t)在[1,2]上单调递减∴g(x)在[1,2]上单调递减证：设0≤x101-2x1-2x2<0∴g(x2)0恒成立∴△=4m2-4(2m2+)<0即>0∴m>或m<-\n（2）令U(x)=x2-2mx+2m2+=(x-m)2+m2=当x=m时U(x)小=m2+∵m2-2>0∴U(x)小=m2-2++2≥4由m2-2=(m2-2)2=1∴m=±此时f(x)小=2x=或-\n谢谢