高中物理精品课件：单摆课件(上课必备) 18页

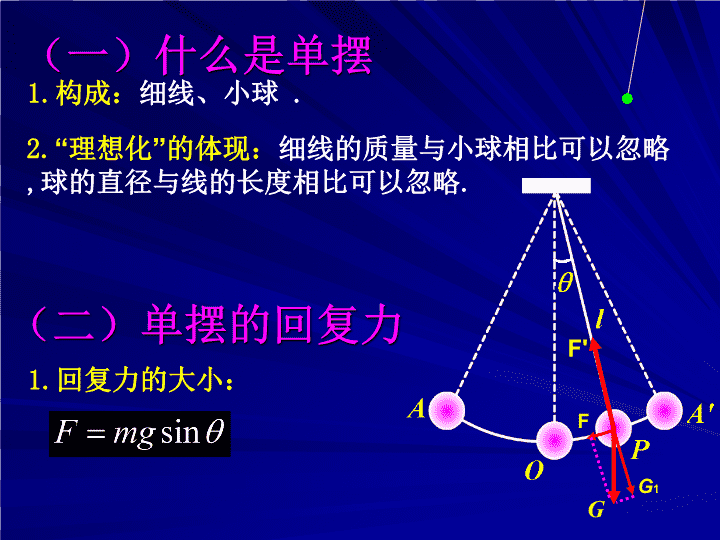
单摆\n秋千摆钟祁阳四中柏国卿\n（一）什么是单摆1.构成：细线、小球.2.“理想化”的体现：细线的质量与小球相比可以忽略,球的直径与线的长度相比可以忽略.（二）单摆的回复力1.回复力的大小：GF'FG1\n当θ很小时F与x方向相反设则有2.单摆作简谐运动的条件：偏角θ很小AOA'\n3.单摆的运动是不是简谐运动呢?受力分析:(1)θ<50时,单摆是简谐运动.(2)单摆振动的回复力是重力的一个分力,不是重力和拉力的合力结论GF'FG1\n（三）单摆的周期1.实验结论：单摆的周期与摆球的质量、运动的振幅无关，但与摆长有关，摆长越长，周期越大.2.周期T与摆长的定量关系：惠更斯，荷兰物理学家、天文学家、数学家，土卫六的发现者，他还发现了猎户座大星云和土星光环，他还设计了用来计时的摆钟。他是介于伽利略与牛顿之间一位重要的物理学先驱。3.单摆的周期公式：\n（四）用单摆测定重力加速度1.实验原理：2.测量仪器:秒表、直尺、游标卡尺.3.图象的斜率:\n荷兰物理学家惠更斯得出:注意事项:(1)摆长l:悬点到球心的距离(2)适用条件:单摆做简谐运动.θ<50(3)利用单摆测重力加速度小结:单摆的周期T（振动周期跟振幅和摆球的质量无关）\n五.单摆振动中的等效问题(1)摆长等效(2)重力加速度等效(3)模型等效\n①等效摆长摆长(或等效摆长)重力加速度(或等效重力加速度)摆球重心到摆动圆弧圆心的距离。o双线摆L\n②等效重力加速度αo例.如图，一小球用长为L的细线系于与水平面成α角的光滑斜面内，小球呈平衡状态。若使细线偏离平衡位置，其偏角小于5o，然后将小球由静止释放，则小球到达最低点所需的时间为多少？不论悬点如何运动或还是受别的作用力，等效重力加速度的取值总是单摆不振动时，摆线的拉力与摆球质量的比值(g=T/m)。\n总结：求等效重力加速度的步骤（1）分析摆球的受力，确定摆球相对静止的位置（即平衡位置）。（2）计算摆球的视重。（即平衡位置的拉力）（3）利用，　　　求出等效重力加速度。\n一单摆，摆长为L，摆球质量为m，悬在升降机顶部，当升降机以加速度a下降时，求：单摆周期T。a等效重力加速度g’=T/m=g-a在平衡位置，且相对静止时（相对升降机），摆绳拉力T=mg-ma解：则变形：若升降机以加速度a上升呢？在超重或失重时单摆处于超重状态时，等效g’=g+a，失重时等效g’=g-a\n如图有一带电量为q的小球，用长为L的绝缘细线悬挂在匀强电场E中，匀强电场方向与重力方向相同，当小球小角度摆动时，求摆动周期。（小球半径为r，重力加速度为g）E变形：若把匀强电场变为水平向右呢？单摆不摆动时在平衡位置，摆绳拉力T=mg+Eq解：则等效重力加速度在复合场中\n不论悬点如何运动或还是受别的作用力，等效重力加速度的取值总是单摆不振动时，摆线的拉力与摆球质量的比值(g=T/m)。等效重力加速度注意：此结论在除去绳子拉力或者等效拉力外，其它力是恒力的情况下普遍适用，否则要由单摆周期的本质来考虑！++例.一单摆的悬点处有一带正电q小球，悬挂的小球也带正电q，摆长为L，小球半径可忽略，求单摆做小角度摆动时的周期。分析：此时小球除去绳子拉力受重力和库仑力，而库仑力方向不断变化！故不能应用所述结论解题。应当考虑此时回复力的变化，看系统的K的变化！\n３、模型等效例.如图所示，光滑圆弧槽半径为R，A为最低点，C到A距离远小于R，两质点B和C都由静止开始释放，问哪一个小球先到A点？讨论：要使两球在A点相遇，可使B球上移，问此时B球高度h为多少？\n小结常见的等效单摆模型很多，上述各图中的模型就是典型的例子。从近几年高考试题看，命题人的指导思想很明确，那就是力求所命题目的创意新、背景新、过程新。但从题目所对应的物理模型来看，其本质上讲还是万变不离其宗。等效法是科学思维的基本方法之一，要提高解决综合问题的能力，从根本上讲还是提高构建物理模型的能力，要学会透过现象看本质，进而对物理模型进行等效转化。\n再见