最新高中抛物线课件 11页

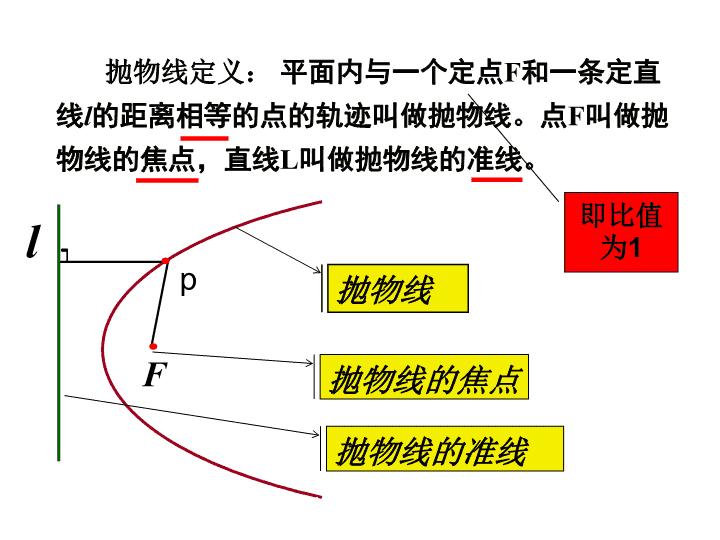
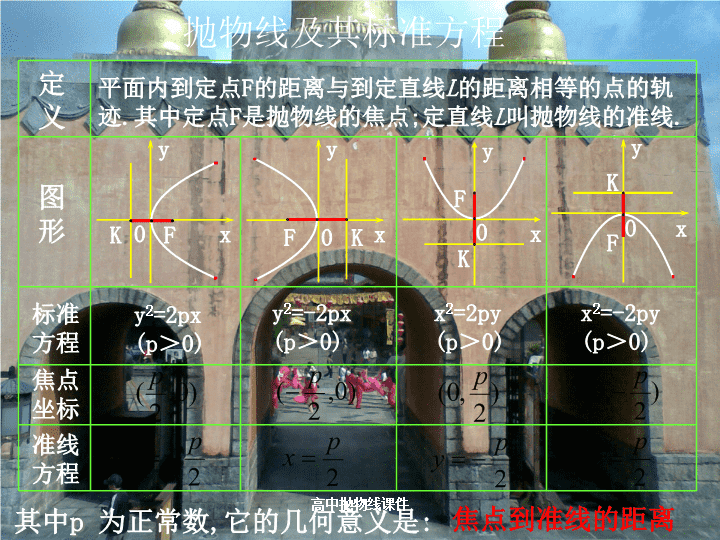
第三讲:抛物线高中抛物线课件\n抛物线定义：平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线。点F叫做抛物线的焦点，直线L叫做抛物线的准线。抛物线抛物线的焦点抛物线的准线即比值为1l┑Fp高中抛物线课件\ny2=-2px(p＞0)x2=2py(p＞0)x2=-2py(p＞0)y2=2px(p＞0)平面内到定点F的距离与到定直线L的距离相等的点的轨迹.其中定点F是抛物线的焦点;定直线L叫抛物线的准线.抛物线及其标准方程定义标准方程焦点坐标准线方程图形其中p为正常数,它的几何意义是:焦点到准线的距离yFK0xFK0xyFK0xyFK0xy高中抛物线课件\n1.抛物线(p>0)的通径(过焦点与对称轴垂直的弦)长为2p.2.已知AB抛物线y2=2px(p>0)的焦点弦,F为焦点,A(x1,y1),B(x2,y2):①|AB|=x1+x2+P②y1y2=-p2③x1x2=④以AB为直径的圆与抛物线准线相切重要结论高中抛物线课件\n例1:已知抛物线的标准方程是y2=6x，求它的焦点坐标和准线方程；变式：已知抛物线的方程是y=－6x2，求它的焦点坐标和准线方程；典型例题:高中抛物线课件\n典型例题:例2:动点P到直线x+4=0的距离减去它到点(2,0)的距离之差等于2,则P点的轨迹方程是:_____________高中抛物线课件\n例3:试分别求满足下列条件的抛物线的标准方程,并求出对应抛物线的焦点和准线方程.(1)过点(-3,2).(2)焦点在直线x-2y-4=0上.典型例题:高中抛物线课件\n练习1.设斜率为2的直线过抛物线的焦点F,且和轴交于点A,则抛物线方程为？则抛物线C的方程为？练习2.已知抛物线C的顶点坐标为原点，焦点在x轴上，直线y=x与抛物线C交于A，B两点，若为的中点，若△OAF(O为坐标原点)的面积为4,高中抛物线课件\n例4:斜率为1的直线经过y2=4x的焦点,与抛物线相交于两点A、B,(1)求线段AB的长.(2)求△AOB的面积。典型例题:抛物线y2=2px的焦点弦AB长公式:|AB|=x1+x2+P|AB|=|x1-x2|高中抛物线课件\nAF0xy例5:在抛物线y2=2x上求一点P,使得P到焦点F与到点A(3,2)的距离之和最小,并求出最小值.Q解:如图,设|PQ|为P到准线的距离则|PF|=|PQ|∴|AP|+|PF|=|AP|+|PQ|∴当A,P,Q共线时,|AP|+|PF|最小即P点坐标为(2,2)时,|AP|+|PF|最小,且最小值为.PPQ典型例题:高中抛物线课件\n练:在抛物线y2=2x上求一点P,使得P到准线与到点A(3,4)的距离之和最小,并求出最小值.典型练习:AF0xyPQ高中抛物线课件