《高中定积分的应用》PPT课件 26页

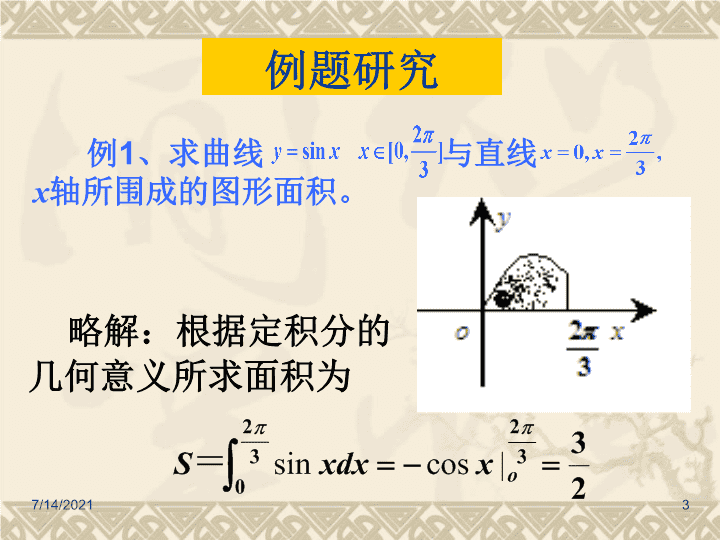
定积分的应用\n问题情境（复习引入）1、求曲边梯形的思想方法是什么？2、定积分的几何意义是什么？3、微积分基本定理是什么？课题：定积分的应用我行我能我要成功我能成功7/14/20212\n例1、求曲线与直线x轴所围成的图形面积。略解：根据定积分的几何意义所求面积为例题研究7/14/20213\n（一）利用定积分求平面图形的面积课题：定积分的应用我行我能我要成功我能成功平面图形的面积平面图形的面积7/14/20214\n平面图形的面积平面图形的面积7/14/20215\n平面图形的面积特别注意图形面积与定积分不一定相等,的图像与轴围成的图形的面积为4,而其定积分为0.如函数7/14/20216\n变式引申：1、求直线与抛物线所围成的图形面积。略解：如图直线与抛物线的交点坐标为（－1，1）和（3，9），则课题：定积分的应用我行我能我要成功我能成功7/14/20217\n变式引申2、求由抛物线及其在点M（0，－3）和N（3，0）处的两条切线所围成的图形的面积。xyoy=－x2+4x-3略解：则在M、N点处的切线方程分别为、（3/2，3）7/14/20218\n变式引申3、在曲线上的某点A处作一切线使之与曲线以及轴所围成的面积为.试求：切点A的坐标以及切线方程.xyOy=x2ABC略解：设切点坐标为则切线方程为切线与x轴的交点坐标为7/14/20219\n则由题可知有所以切点坐标与切线方程分别为课题：定积分的应用xyOy=x2ABC7/14/202110\n（1）画图,并将图形分割为若干个曲边梯形；（2）对每个曲边梯形确定其存在的范围,从而确定积分的上、下限；（3）确定被积函数；（4）求出各曲边梯形的面积和,即各积分的绝对值的和。小结:求平面图形面积的方法与步骤：课题：定积分的应用我行我能我要成功我能成功7/14/202111\n型区域：以及(1)曲线与直线轴所围成的曲边梯形的面积：以及(2)曲线与直线轴所围成的曲边梯形的面积：yabxyabxb课题：定积分的应用我行我能我要成功我能成功几种常见的曲边梯形面积的计算方法：7/14/202112\n(3)两条曲线与直线围成的曲边梯形的面积:yaxbyabxb7/14/202113\nyabxaabbyyxx型区域：课题：定积分的应用我行我能我要成功我能成功可由先求出然后利用求出可由先求出然后用求出用求7/14/202114\n变式引申4、求曲线与曲线以及轴所围成的图形面积。略解：如图由得当时则所求图形的面积为由得课题：定积分的应用我行我能我要成功我能成功7/14/202115\n（二）定积分在物理中应用(1)求变速直线运动的路程例题研究v/m/st/s10406030OABC7/14/202116\n例4、A、B两站相距7.2km,一辆电车从A站开往B站,电车开出ts后到达途中C点,这一段的速度为1.2t(m/s),到C点的速度为24m/s,从C点到B点前的D点以等速行驶,从D点开始刹车,经ts后,速度为(24-1.2t)m/s,在B点恰好停车,试求（1）A、C间的距离;（2）B、D间的距离;（3）电车从A站到B站所需的时间。7/14/202117\n略解:(1)设A到C的时间为t1则1.2t=24,t1=20(s),则AC＝(2)设D到B的时间为t2则24-1.2t2=0,t2=20(s),则DB＝（3）CD=7200-2240=6720(m),则从C到D的时间为280(s),则所求时间为20+280+20=320（s）说明：作变速直线运动的物体所经过的路程s,等于其速度函数v=v(t)(v(t)≥0)在时间区间[a,b]上的定积分,即7/14/202118\n(2)变力沿直线所做的功例4：如果1N能拉长弹簧1cm,为了将弹簧拉长6cm,需做功（）A.0.18JB.0.26JC.0.12JD.0.28J所以做功就是求定积分则由题可得。略解：设A说明：物体在变力F(x)的作用下做直线运动，并且物体沿着与F(x)相同的方向从x=a点移动到x=b点，则变力F(x)所做的功为:7/14/202119\n解两曲线的交点oxyABCDO7/14/202120\n解两曲线的交点直线与x轴交点为(4,0)S1S27/14/202121\n解两曲线的交点827/14/202122\n解两曲线的交点7/14/202123\n于是所求面积说明：注意各积分区间上被积函数的形式．7/14/202124\n例2:求由曲线所围成的图形绕轴旋转所得旋转体的体积。例题研究(三)利用定积分求曲边旋转体的体积xyox=1分析：（1）分割;(2)以直代曲；（3）求和；(4)逼近。课题：定积分的应用7/14/202125\n变式引申:某电厂冷却塔外形如图所示,双曲线的一部分绕其中轴(双曲线的虚轴)旋转所成的曲面，其中A,A’是双曲线的顶点，C,C’是冷却塔上口直径的两个端点，B,B’是下底直径的两个端点，已知AA’=14m,CC’=18m,BB’=22m,塔高20m.(1)建立坐标系，并写出该曲线方程．(2)求冷却塔的容积（精确到10m3塔壁厚度不计，取3.14）ＡＣＢＡ’Ｃ’Ｂ’7/14/202126