高中物理力的分解课件 18页

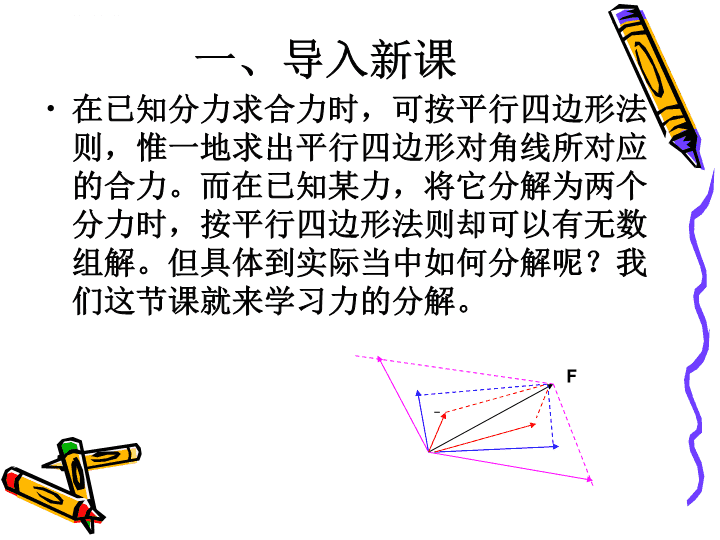
力的分解蔡丽华\n一、导入新课在已知分力求合力时，可按平行四边形法则，惟一地求出平行四边形对角线所对应的合力。而在已知某力，将它分解为两个分力时，按平行四边形法则却可以有无数组解。但具体到实际当中如何分解呢？我们这节课就来学习力的分解。F\n知识点1、理解力的分解是力的合成的逆运算2、知道力的分解要从实际情况出发3、会用图示法根据实际要求运用平行四边形定则求分力。\n1、请同学阅读课本，回答（1）什么是分力？什么是力的分解？（2）为什么说力的分解是力的合成的逆运算？\n某一个力F，可用F1和F2来代替，那这两个力叫F的分力。求一个已知力的分力叫力的分解。如何分解？力的分解是力的合成的逆运算，同样遵守平行四边形定则.把一个力（合力）F作为平行四边形的对角线，然后依据力的效果画出两个分力的方向，进而作出平行四边形，就可得到两个分力F1和F2.\n力的分解的一般方法⑴根据力的作用效果确定两个分力的方向⑵根据已知力和两个分力方向作平行四边形⑶根据平行四边形或三角形知识确定分力的大小和方向。\n总结：分力与合力是在相同作用效果的前提下才能相互替换，所以在分解某力时，其各个分力必须有各自的实际效果，比如：形变效果，在这个意义上讲，力的分解是唯一的。\n分力的唯一性条件（1）已知两个分力的方向，求分力.将力F分解为沿OA、OB两个方向上的分力时，可以从F矢端分别作OA、OB的平行线，即可得到两个分力F1和F2.如图3所示.FAB\n（2）已知一个分力的大小和方向，求另一个分力.已知合力F及其一个分力F1的大小和方向时，先连接F和F1的矢端，再过O点作射线OA与之平行，然后过合力F的矢端作分力F1的平行线与OA相交，即得到另一个分力F2，如图4所示.OFF1AF2\n（3）已知一个分力的方向和另一个分力的大小（如图7）.nFF1AOF2mF2\n已知合力F、分力F1的方向OA及另一个分力F2的大小时，先过合力F的矢端作OA的平行线mn，然后以O为圆心，以F2的长为半径画圆，交mn，若有两个交点，则有两解（如图5），若有一个交点，则有一个解（如图6），若没有交点，则无解OFF1AF2m\n无解OAFF1\n（四）分力方向的确定：一个已知力究竟分解到哪两个方向上去,要根据实际情况，由力的效果来决定.\n例1：放在水平面上的物体受到一个斜向上方的拉力F，这个力与水平方向成θ角，求这个力的两个分力？~该力产生两个效果：1.水平向前拉物体，2.竖直向上提物体，因此力F可以分解为沿水平方向的分力F1和沿竖直方向的分力F2.力F1、F2的大小为F1=cosθ,F2=Fsinθ.F\n把一个物体放在斜面上，物体受到竖直向下的重力，求重力的分力？但它并不能竖直下落，而要沿着斜面下滑，同时使斜面受到压力，重力产生两个效果：1。使物体沿斜面下滑2.使物体紧压斜面，因此重力G可以分解为平行于斜面使物体下滑的分力F1和垂直于斜面使物体紧压斜面的分力F2.G\n【例2】如图1-6-3所示，用绳将重球挂在光滑墙上，求球对墙的压力和绳子中张力。【解析】将重球受到重力进行分解，重力产生两个效果。1.使绳绷紧产生形变，由于绳的形变沿绳的方向，故重力作用的这个效果用重力沿绳方向的分力G1来表示2.重力作用使球水平向左挤压竖直墙面，使墙产生形变，重力的这一效果用垂直接触面沿OQ方向的分力G2表示，作出平行四边形。由力的平行四边形定则得：G1=G/COSθG2=GtgθG1G2GOθ图1-6-3\n综上所述：虽然一个力可以分解为无数对力，但在具体问题中，一定要按照力的效果分解，才是合理的分解.\n（五）课堂小结原则：根据力的实际作用效果分解方法：平行四边形定则（解三角形）类型：（1）已知两个分力的方向（唯一解）（2）已知一个分力的大小和方向（唯一)（3）已知一个分力的方向和另一个分力的大小（两解、一解或无解）