高中数学核动力课件 33页

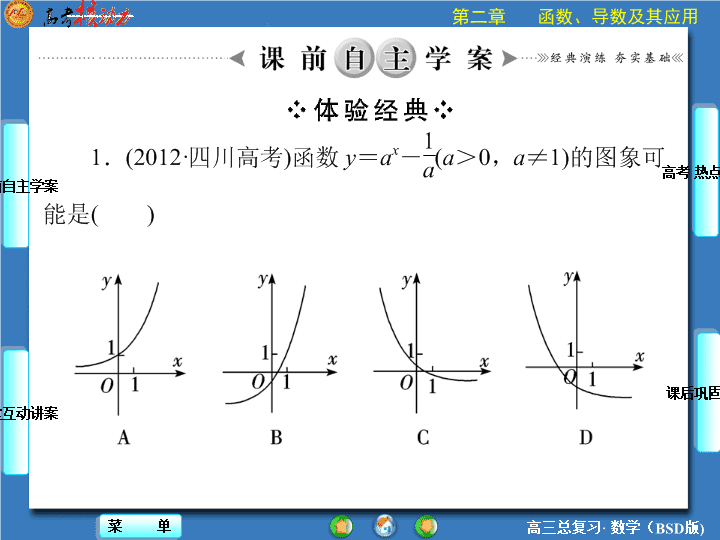
\n\n【答案】D\n\n【答案】A\n3．下列四类函数中，具有性质“对任意的x>0，y>0，函数f(x)满足f(x＋y)＝f(x)f(y)”的是(　　)A．幂函数　　　　　B．对数函数C．指数函数D．余弦函数【解析】A项，f(x)＝xa，f(x＋y)＝(x＋y)a≠f(x)·f(y)＝xa·ya；B项，f(x)＝logax，loga(x＋y)≠logax·logay；C项，f(x)＝ax，则ax＋y＝ax·ay；D项，f(x)＝cosx，cos(x＋y)≠cosx·cosy.【答案】C\n4．(2012·上海高考)方程4x－2x＋1－3＝0的解是________．【解析】原方程可化为(2x)2－2·2x－3＝0，解得2x＝3，或2x＝－1(舍去)，∴x＝log23.【答案】log23\n\n1．根式(1)根式的概念\n\n1．分数指数幂与根式有何关系？提示：分数指数幂与根式可以互化，通常利用分数指数幂进行根式的运算.\n\n3．指数函数的图象与性质\n\n2．如图是指数函数(1)y＝ax，(2)y＝bx，(3)y＝cx，(4)y＝dx的图象，如何确定底数a，b，c，d与1之间的大小关系．提示：在图中作出直线x＝1，与它们图象交点的纵坐标即为它们各自底数的值，即c＞d＞1＞a＞b，所以无论在y轴的右侧还是左侧，底数按逆时针方向依次变大.\n\n【思路点拨】先化为分数指数幂，再进行运算．\n【归纳提升】指数幂的化简与求值的原则及结果要求1．化简原则(1)化负指数为正指数；(2)化根式为分数指数幂；(3)化小数为分数；(4)注意运算的先后顺序．\n2．结果要求(1)若题目以根式形式给出，则结果用根式表示；(2)若题目以分数指数幂的形式给出，则结果用分数指数幂表示；(3)结果不能同时含有根号和分数指数幂，也不能既有分母又有负指数幂.\n(2013·信阳模拟)函数f(x)＝ax－b的图象如图所示，其中a、b为常数，则下列结论正确的是(　　)\nA．a＞1，b＜0　　　B．a＞1，b＞0C．0＜a＜1，b＞0D．0＜a＜1，b＜0【思路点拨】(1)由图象看到单调递减函数，所以底数0＜a＜1，(2)根据图象平移得b的范围．【尝试解答】由图象得函数是减函数，∴0＜a＜1.又分析得，图象是由y＝ax的图象向左平移所得，∴－b＞0，即b＜0.从而D正确．【答案】D\n【归纳提升】抓住指数函数的图象，不仅可以直观准确地把握指数函数的性质，而且利用指数函数的图象的形象直观，还可以使有些问题得到简捷的解法.\n设a＞0且a≠1，函数y＝a2x＋2ax－1在[－1,1]上的最大值是14，求a的值．【思路点拨】换元令t＝ax，利用二次函数和指数函数的单调性来研究函数的单调性，构建方程获解．【尝试解答】令t＝ax(a＞0且a≠1)，则原函数化为y＝(t＋1)2－2(t＞0)．\n\n【归纳提升】指数函数问题一般常与其它函数复合．本题利用换元法将原函数化为二次函数，结合二次函数的单调性和指数函数的单调性判断出原函数的单调性，从而获解．由于指数函数的单调性取决于底数的大小，所以要注意对底数的分类讨论，避免漏解．\n●考情全揭密●从近几年高考对指数函数和指数型函数的考题来看，指数函数的概念、图象与性质是近几年高考的热点，通过具体问题考查指数函数的图象与性质，或利用指数函数的图象与性质解决一些实际问题是重点，也是难点，同时考查分类讨论思想和数形结合思想，题型以选择题和填空题为主，与其他知识点交汇则以解答题的形式出现．2014年的高考中仍应以指数函数的性质应用为主，同时关注解答题与导数的融合．\n\n(2012·上海高考)已知函数f(x)＝e|x－a|(a为常数)．若f(x)在区间[1，＋∞)上是增函数，则a的取值范围是________．【规范解答】令t＝|x－a|，则t＝|x－a|在区间[a，＋∞)上单调递增，而y＝et为增函数，所以要是函数f(x)＝e|x－a|在[1，＋∞)单调递增，则有a≤1，所以a的取值范围是(－∞，1]．【答案】(－∞，1]\n【解】(1)由2x－1≠0，可解得x≠0，∴定义域为{x|x≠0}．\n\n\n\n本小节结束请按ESC键返回