统计与概率重点高中课件 27页

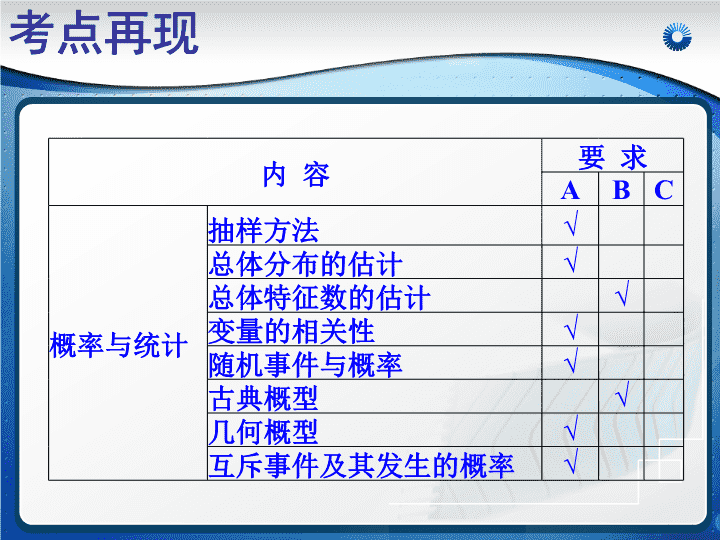
同学们,当老师提问或请同学们练习时，你可以按播放器上的暂停键思考或练习，然后再点击播放键.\n统计与概率江苏省扬中高级中学陆昌荣审稿镇江市教研室黄厚忠统计与概率\n内容要求ABC概率与统计抽样方法√总体分布的估计√总体特征数的估计√变量的相关性√随机事件与概率√古典概型√几何概型√互斥事件及其发生的概率√考点再现\n类别各自特点相互联系适用范围简单随机抽样系统抽样分层抽样从总体中逐个抽取将总体均分成几部分，按事先确定的规则在各部分抽取将总体分成几层，分层进行抽取在起始部分抽样时采用简单随机抽样各层抽样时采用简单随机抽样或系统抽样总体中的个体数较少总体中的个体数较多1、抽样方法总体由差异明显的几部分组成共同点抽样过程中每个个体被抽到的可能性相同知识回顾一\n知识回顾一2、总体分布的估计样本的频率分布表样本的频率分布直方图样本的茎叶图\n一般地，作频率分布直方图的步骤如下：（1）求全距，决定组数和组距；全距是指整个取值区间的长度，组距是指分成的区间的长度;（2）分组，通常对组内的数值所在的区间取左闭右开区间，最后一组取闭区间；（3）登记频数，计算频率，列出频率分布表;（4）画出频率分布直方图（纵轴表示频率／组距）.总体分布的估计\n知识回顾一3、总体特征数的估计设一组样本数据，方差标准差均值\nxx1x2x3…xnyy1y2y3…yn线性回归方程知识回顾一4、线性回归方程点满足方程),(yx\n系统抽样利用简单随机抽样,剔除4人例1:(1)选取学生代表开座谈会时，请学号末位数为6的同学参加.则这种抽样方法是___________.(2)某单位共有在岗职工人数为624人,为了调查工人上班平均所用时间,决定抽取10%的工人调查这一情况,如果采用系统抽样方法完成这一抽样,则首先_______________________________.(3)某中学有高一学生400人,高二学生320人,高三学生280人,以每人被抽取的概率为0.2向该中学抽取一个容量为n的样本,则n=___________.200典型例题一\n例2:有一容量为100的样本,数据的分组以及各组的频数如下:[12.5,15.5),6;[15.5,18.5),16;[18.5,21.5),18;[21.5,24.5),22;[24.5,27.5),20;[27.5,30.5),10;[30.5,33.5],8;(1)列出样本的频率分布表(2)画出频率分布直方图典型例题一\n解:(1)样本的频率分布表如下:分组频数频率频率/组距12.5~15.560.060.0215.5~18.5160.160.05318.5~21.5180.180.0621.5~24.5220.220.07324.5~27.5200.200.06727.5~30.5100.100.03330.5~33.580.080.027合计1001.00典型例题一\n(2)频率分布直方图:数据频率组距12.515.518.521.524.527.530.533.5典型例题一\n例3:某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数与实际平均数的差是________例4:数据平均数为6，标准差为2，则数据的平均数为，方差为。典型例题一-3616小结：若数据的均值为，方差为x2snxxxL,,21则数据的均值为，方差为。baxbaxbaxn+++,,,21L\n1、随机事件及其发生的概率随机事件(A)、必然事件(Ω)、不可能事件(φ)对于给定的随机事件A，如果随着试验次数的增加，事件A发生的频率fn(A)稳定在某个常数上，把这个常数记做P(A)称为事件A的概率。0≤P（A）≤1；P(Ω)＝1，P(φ)=0.知识回顾二\n知识回顾二2、古典概型(1)有限性：在随机试验中，其可能出现的结果有有限个，即只有有限个不同的基本事件；(2)等可能性：每个基本事件发生的机会是均等的.件的个数样本空间包含的基本事包含的基本事件的个数随机事件nmA)(==Ap\n知识回顾二3、几何概型(1)有一个可度量的几何图形S；(2)试验E看成在S中随机地投掷一点；(3)事件A就是所投掷的点落在S中的可度量图形A中．P(A)=\n知识回顾二4、互斥事件ABI互斥事件：不可能同时发生的两个事件.A对立事件：必有一个发生的互斥事件.事件A的对立事件记为事件A,B为互斥事件，则P(A+B)=P(A)+P(B)P(A)＋P()＝P(A＋)＝1\n例1:从含有两件正品a,b和一件次品c的三件产品中每次任取1件，每次取出后不放回，连续取两次，求取出的两件中恰好有一件次品的概率。解：每次取一个，取后不放回连续取两次，其样本空间是Ω={}(a,b),(a,c),(b,a),(b,c),(c,a),(c,b)∴n=6用A表示“取出的两件中恰好有一件次品”这一事件，则A={}(a,c),(b,c),(c,a),(c,b)∴m=4∴P(A)=典型例题二\n典型例题二变题1:从含有两件正品a,b和一件次品c的三件产品中每次任取1件，每次取出后放回，连续取两次，求取出的两件中恰好有一件次品的概率。解：每次取一个，取后放回连续取两次，其样本空间是Ω={}(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)∴n=9用B表示“恰有一件次品”这一事件，则B={}(a,c),(b,c),(c,a),(c,b)∴m=4∴P(B)=\n典型例题二变题2:从含有两件正品a,b和一件次品c的三件产品中任取2件，求取出的两件中恰好有一件次品的概率。解：试验的样本空间为Ω={ab,ac,bc}∴n=3用A表示“取出的两件中恰好有一件次品”这一事件，则A={ac,bc}∴m=2∴P(A)=小结：1.判断是否为古典概型；2.用“枚举法”准确计算出基本事件总数和事件A包含的基本事件数。\n典型例题二例2:在等腰直角三角形ABC中，在斜边AB上任取一点M，求AM小于AC的概率．C’ACBM解：在AB上截取AC’＝AC，故AM＜AC的概率等于AM＜AC’的概率．记事件A为“AM小于AC”，答：AM＜AC的概率等于\n典型例题二变题:在等腰直角三角形ABC中，过直角顶点C作射线CM交AB于M，求AM小于AC的概率．ACBM解：在AB上截取AC’＝AC，故“AM＜AC”的概率等于“CM落在∠ACC’内部”的概率．记事件B为“AM小于AC”，答：AM＜AC的概率等于C’小结：几何概型解题的关键是找准测度\n典型例题二例3：在3名男生和2名女生中，任选2名，求恰好是2名男生或2名女生的概率.解：记“从中任选2名，恰好是2名男生”为事件A，“从中任选2名，恰好是2名女生”为事件B，则事件A与事件B为互斥事件，且“从中任选2名，恰好是2名男生或2名女生”为事件A+B.答：从中任选2名，恰好是2名男生或2名女生的概率为2/5.\n典型例题二变题：在3名男生和2名女生中，任选2名，求至少有1名男生的概率.解一：记“从中任选2名，恰好1名男生和一名女生”为事件A，“从中任选2名，恰好是2名男生”为事件B，则事件A与事件B为互斥事件，且“从中任选2名，至少有1名男生”为事件A+B.答：从中任选2名，恰好是2名男生或2名女生的概率为9/10.\n典型例题二变题：在3名男生和2名女生中，任选2名，求至少有1名男生的概率.答：从中任选2名，恰好是2名男生或2名女生的概率为9/10.解二：记“从中任选2名，恰好2名女生”为事件A，则“从中任选2名，至少有1名男生”为事件.小结：在求某些稍复杂的事件的概率时，通常有两种方法：一是将所求事件的概率化成一些彼此互斥的事件的概率的和，二是先去求此事件的对立事件的概率.正难则反的思想\n课堂小结课堂小结本节课主要复习了抽样方法、总体特征数的估计，古典概型、几何概型以及互斥事件的概率，同时同学们要注意枚举法在古典概型中的运用，以及正难则反的思想在解题中的应用。课堂小结\nEND祝同学们学习进步再见！