高中数学参赛课件 幂函数 12页

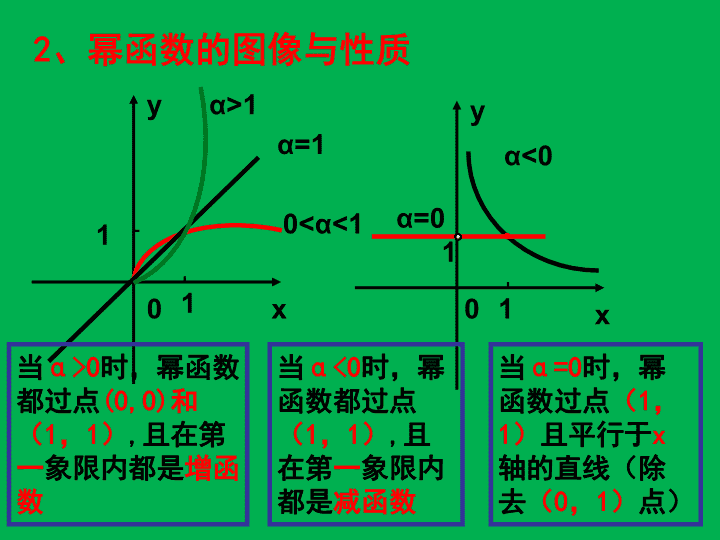
幂函数\n一、知识归纳1.定义：形如y=xα（α为常数）的函数叫做幂函数强调1：如：y=2x2,y=3x-2这些不是幂函数强调2：指数函数与幂函数的区别：看变量x在指数上还是底数上强调3：要确定一个幂函数，需要一个条件就可以，即把常数确定下来。\n2、幂函数的图像与性质0xy0<α<1α=1α>1110xy11α<0当α>0时，幂函数都过点(0,0)和（1，1）,且在第一象限内都是增函数当α<0时，幂函数都过点（1，1）,且在第一象限内都是减函数当α=0时，幂函数过点（1，1）且平行于x轴的直线（除去（0，1）点）α=0\n3、根据幂函数的图像比较大小重要结论:在区间(1,+∞)上,幂函数的指数越大,图像越高,在（0，1）上，幂函数的指数越大图像越低\n题型一：幂函数概念例1（1）下列函数中不为幂函数的为（）A．B．C．D．（2）下列命题中，正确命题的序号是①当时，函数的图象是一条直线；②幂函数的图象都经过（0，0）和（1，1）点；③若幂函数是奇函数，则是定义域上的增函数；④幂函数的图象不可能出现在第四象限．\n（2）已知幂函数的图象不过原点，则m的值为______。例2（1）函数的定义域是（）A．{x|x≠0或x≠2}B．（－∞，0）（2，＋∞）C．（－∞，0）［2，＋∞　）D．（0，2）\n例3(1)当x∈（1，+∞）时，函数的图象恒在y=x的下方，则的取值范围是_________。（2）(2011.上海)右下图为幂函数在第一象限的图象，则按由小到大的顺序排列为.题型二：幂函数图象性质\n例4幂函数，当取不同的正数时，在区间上它们的图象是一族美丽的曲线（如图），设点A(1,0),B(0,1)，连结AB，线段AB恰好被其中的两个幂函数的图象三等分，即有BM=MN=NA。那么\n题型三：比较大小例5（1）若，比较的大小；（2）若比较的大小．\n题型四：幂函数的综合应用例6．已知幂函数的图象与x轴、y轴都无交点，且关于y轴对称，试确定的解析式．\n备用：已知函数（1）求函数的定义域、值域；（2）判断函数的奇偶性；（3）求函数的单调区间.\n作业:1.比较下列各数的大小3.已知函数为偶函数，且f(3)