【高中数学课件】欧拉公式1 ppt课件 14页

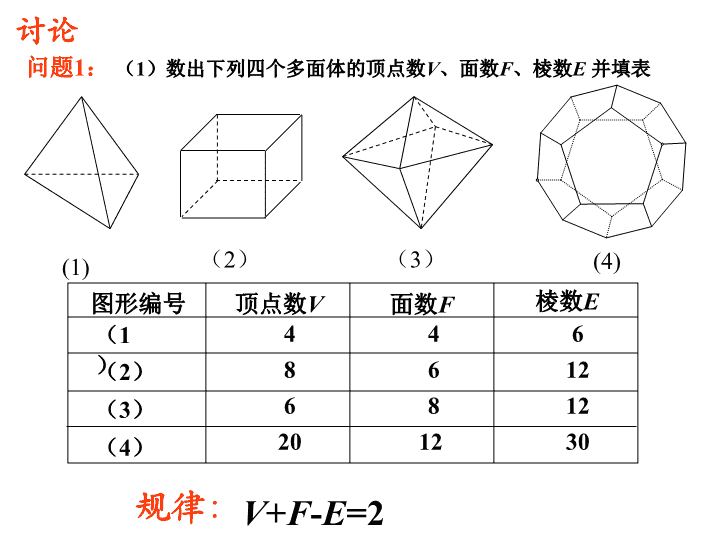
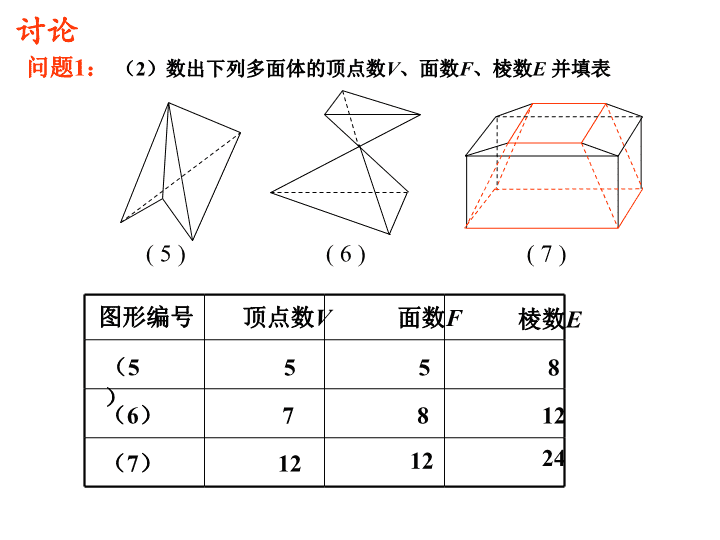
著名的数学家，瑞士人，大部分时间在俄国和法国度过．他17岁获得硕士学位，早年在数学天才贝努里赏识下开始学习数学，毕业后研究数学，是数学史上最高产的作家．在世发表论文700多篇，去世后还留下100多篇待发表．其论著几乎涉及所有数学分支．他首先使用f(x)表示函数，首先用∑表示连加，首先用i表示虚数单位．在立体几何中多面体研究中，首先发现并证明欧拉公式．欧拉欧拉公式及其应用\n讨论问题1：（1）数出下列四个多面体的顶点数V、面数F、棱数E并填表(1)（2）（3）图形编号顶点数V面数F棱数E（1）（2）（3）（4）规律：V+F-E=246486126812201230(4)\n(6)问题1：（2）数出下列多面体的顶点数V、面数F、棱数E并填表讨论(5)5857812图形编号顶点数V面数F棱数E（5）（6）121224（7）(7)\n多面体简单多面体表面经过连续变形能变成一个球面的多面体V+F-E=2简单多面体欧拉公式欧拉示性数：在欧拉公式中令，叫欧拉示性数\n问题2：如何证明欧拉公式ABCDEA1B1C1D1E1ABCDEA1B1C1D1E1讨论压缩成平面图形\n问题2：如何证明欧拉公式ABCDEA1B1C1D1E1ABCDEA1B1C1D1E1讨论压缩成平面图形\n思考1：多面体的面数是F，顶点数是V，棱数是E，则平面图形中的多边形个数、顶点数、边数分别为思考2：设多面体的F个面分别是n1,n2,···,nF边形，各个面的内角总和是多少？(n1-2)·1800+(n2-2)·1800+···+(nF-2)·1800=(n1+n2+···+nF-2F）·1800思考3：n1+n2+···+nF和多面体的棱数E有什么关系n1+n2+···+nF=2EF、V、E．问题2：如何证明欧拉公式讨论ABCDEA1B1C1D1E1ABCDEA1B1C1D1E1压缩成平面图形\n∴所有面的内角和=（E－F）·3600思考4：设平面图形中最大多边形（即多边形ABCDE）是m边形，则它和它内部的全体多边形的内角总和是多少？2（m-2)·1800+(V-m)·3600=(V-2)·3600∴（E-F）·3600=(V-2)·3600问题2：如何证明欧拉公式讨论ABCDEA1B1C1D1E1ABCDEA1B1C1D1E1V+F-E=2欧拉公式压缩成平面图形\n欧拉公式的应用例11996年的诺贝尔化学奖授予对发现C60有重大贡献的三位科学家．C60是有60个C原子组成的分子，它结构为简单多面体形状．这个多面体有60个顶点，从每个顶点都引出3条棱，各面的形状分别为五边形或六边形两种．计算C60分子中形状为五边形和六边形的面各有多少？解：设C60分子中形状为五边形和六边形的面各有x个和y个．由题意有顶点数V=60，面数=x+y，棱数E=（3×60）\n问题3:欧拉公式的应用例11996年的诺贝尔化学奖授予对发现C60有重大贡献的三位科学家．C60是有60个C原子组成的分子，它结构为简单多面体形状．这个多面体有60个顶点，从每个顶点都引出3条棱，各面的形状分别为五边形或六边形两种．计算C60分子中形状为五边形和六边形的面各有多少？解：设C60分子中形状为五边形和六边形的面各有x个和y个．由题意有顶点数V=60，面数=x+y，棱数E=（3×60）根据欧拉公式，可得60+（x+y)－（3×60）=2另一方面，棱数也可由多边形的边数来表示，即（5x+6y)=（3×60）由以上两个方程可解出x=12,y=20答：C60分子中形状为五边形和六边形的面各有12个和20个．\n例2、有没有棱数是7的简单多面体？解：假设有一个简单多面体的棱数E=7．根据欧拉公式得V+F=E+2=9因为多面体的顶点数V≥4，面数F≥4，所以只有两种情形：V=4，F=5或V=5，F=4．但是，有4个顶点的多面体只有4个面，而四面体也只有四个顶点．所以假设不成立，没有棱数是7的简单多面体问题3:欧拉公式的应用\n1、（1）一个简单多面体的各面都是三角形，证明它的顶点数V和面数F有F=2V－4的关系．练习（2）若简单多面体的各面都是四边形，则它的顶点数V和面数F又有怎样的关系？2、简单多面体的每个面都是五边形，且每个顶点的一端都有三条棱，求这个多面体的面数和棱数．F=V-2F=12E=30\n小结猜想证明应用空间问题平面化作业P68阅读材料V+F-E=2欧拉公式\n