【高中数学课件】直线与平面垂直ppt课件 40页

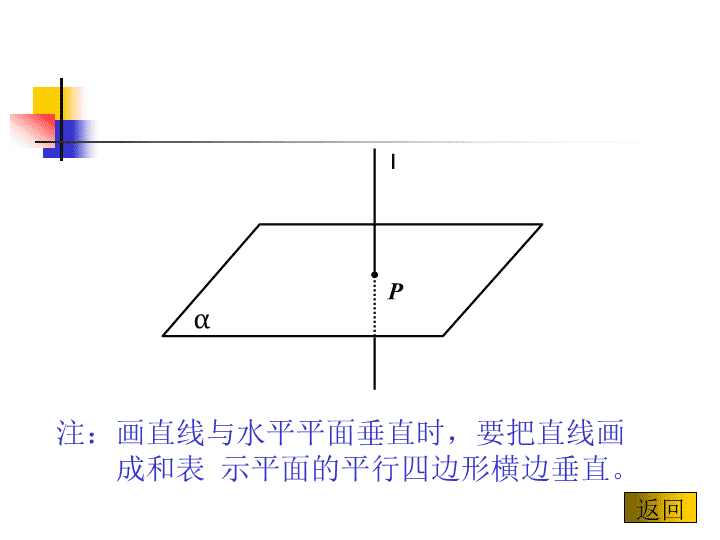
直线与平面垂直的判定\n一、直线与平面垂直的定义如果一条直线l和一个平面α内的任意一条直线都垂直，我们就说直线l和平面α互相垂直，记作l⊥α。（如图）直线l叫做平面α的垂线。平面α叫做直线l的垂面。直线l和平面α的交点叫做垂足。\nαPl注：画直线与水平平面垂直时，要把直线画成和表示平面的平行四边形横边垂直。返回\n二、直线和平面垂直的判定定理如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。\n三、线面垂直判定定理的证明已知：mα，nα，m∩n=B，l⊥m，l⊥n。求证：l⊥α。\nαmnBl\nαmnBll\nαmnBl\nlαmngB\nlαmngBg\nlαmnBgAA’AB=A’B\nlαmnBgAA’AB=A’B\nlαmnBgAA’AB=A’B\nlαmnBgAA’\nlαmngABA’CDE\nlαmngABCDA’E\nlαmngABCDA’El⊥m\nlαmABCA’l⊥m\nlαmABCA’l⊥mAC=A’C\nlαmngABCDA’EAD=A’D\nlαmngABCDA’ECD=CD\nlαmngABCDA’E△ACD≌△A’CD\nlαmngABCDA’E∠ACE=∠A’CE\nlαmngABCDA’EAC=A’CCE=CE\nlαmngABCDA’E△ACE≌△A’CE\nlαmngABCDA’EAE=A’E\nlαmngABCDA’EAE=A’EAB=A’B\nlαgABA’EAE=A’EAB=A’B\nlαgABA’EAE=A’EAB=A’Bl⊥g\n如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。直线和平面垂直的判定定理注：mαnαm∩n=Bl⊥ml⊥nl⊥α\n这个定理还说明这样一个事实，的确存在着和一个平面内一切直线都垂直的直线，从而得证了直线和平面垂直的合理性。这个定理不仅提供了判定直线和平面垂值得一种方法，而且还是证明直线和直线互相垂直的一种常用的方法，即要想证明a⊥b，只需证a与b所在平面内的两条相交直线垂直（或证b与a所在平面内的两条相交直线垂直）。小结\n1、如果一条直线垂直于平面内的一条直线，能否判断这条直线和这个平面垂直？2、如果一条直线垂直于平面内的两条直线，能否判断这条直线和这个平面垂直？3、如果一条直线垂直于平面内的无数条直线，能否判断这条直线和这个平面垂直？练习\n4、如果三条直线共点、且两两垂直，其中任一条直线是否垂直于另两条直线确定的平面？为什么？5、如果一条直线垂直于一个三角形的两边，能否断定这条直线和三角形的第三条边垂直？为什么？练习\nαabmn已知：a∥b，a⊥α求证：b⊥α例1如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于同一个平面。（此定理可看作线面垂直的判定公理二）\n证明：在平面α内作两条相交直线m，n∵a⊥α∴a⊥m,a⊥n∵b∥a∴b⊥m，b⊥n∴b⊥ααabmn\nαβγabcE例2已知：bα，cα,b∩c=E，β∩γ=a，c⊥β，d⊥γ。求证：a⊥α。\n证明：∵b⊥β，β∩γ=a，∴b⊥a；∵c⊥γ，β∩γ=a，∴c⊥a；∵b∩c=E，bα，cα,∴a⊥α。αβγabcE\n例3已知：正方体中，AC是面对角线，BD’是与AC异面的体对角线。求证：AC⊥BD’ABDCA’B’C’D’\n证明：连接BD∵正方体ABCD-A’B’C’D’∴DD’⊥正方体ABCD∵AC、BD为对角线∴AC⊥BD∵DD’∩BD=D∴AC⊥△D’DB∴AC⊥BD’ABDCA’B’C’D’\nlαmngABCDA’E