2018陕西高中数学竞赛预赛试题(含答案)-高中课件精选 8页

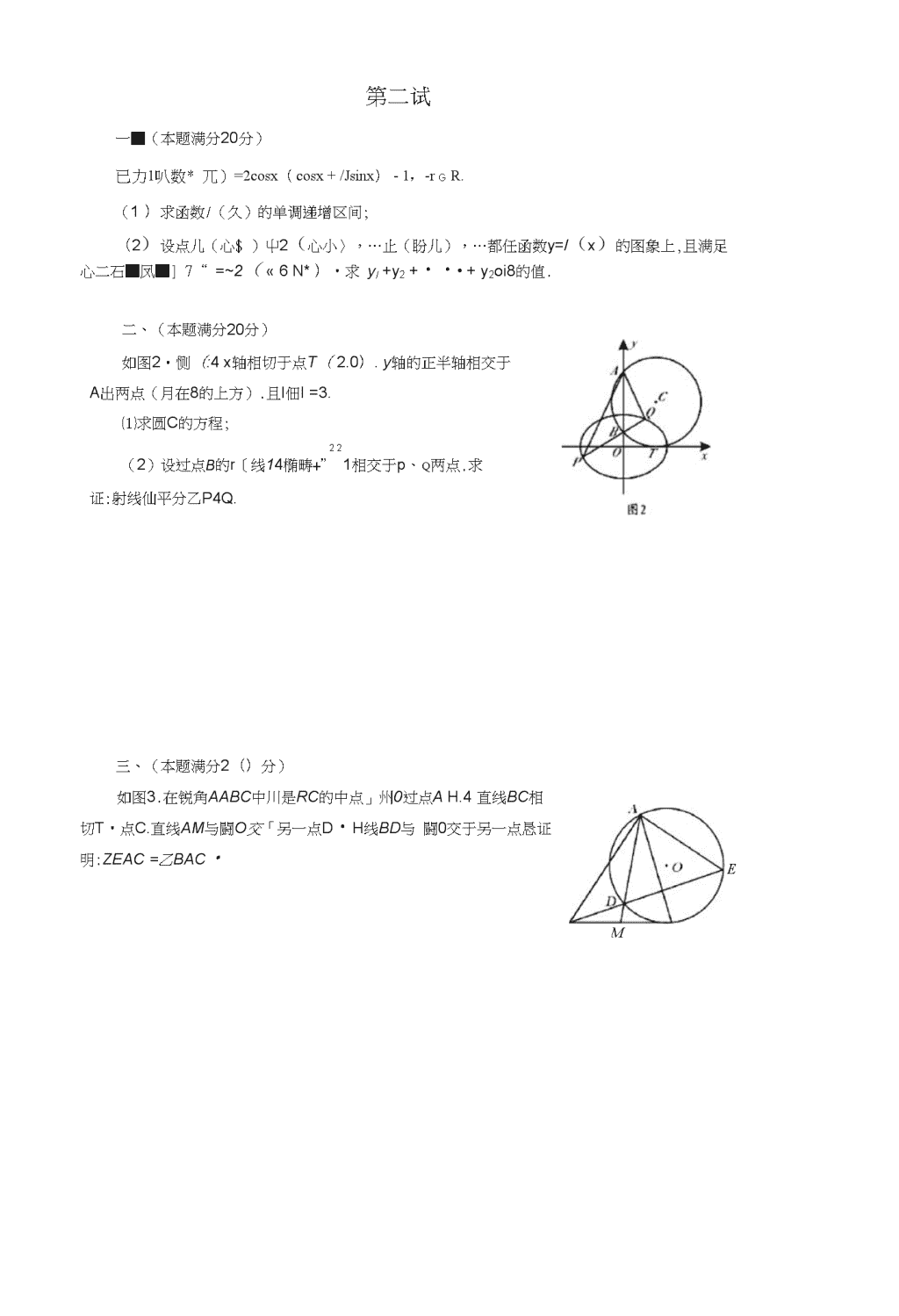
2018年全国高中数学联赛陕西赛区预赛试题2018.4.15考生注意：1.本试卷分两斌.第一斌共两大題•满分80分：第二试淇五大期•满分120分.2•用蓝色｛或黑色）钢笔、蒋字笔或圖珠笔作签.3.解題书写不要趙过除订线.4.不能使用计算器.第一试一、选择题：本题共8小题,每小题6分，共48分•在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合.W={xl.x=sin''巴§彳FwZ.=］y|y=cos号』eZ，则MHN的爻系是()A.M宇/VB.W=/VC.N^MD.Mr\N=4>2.Ll531a=logfi5.b=10^3.t*=亍•则a、b、c的大小关系是()A.(i>h>cB・b>c>aC.b>a>cF).c>b>a3.lL知数列叫：满足«)=I.an>1=n+1+(neN*)./f1x_/x(p>())的矢点为八准线为I、过点F的建线丄j抛物线交J：A、B两点,H.IABI=3p・设点A、B任II:的射影分別为.VH，今向卩q边形AA'^H内任投一点M，则点M落在△心'〃'内的燧率是-11.L.知阴数/(尤)=*+十■1・若存在X)七.…牝€［土4］.使㈣(曲)+/(也)+…+/(xB_l)=/("・则正整数〃的最大值是.12•设/I是止整数.当n>KX)111.灯+3几+1的小数部分的前两位数是\n第二试EM一■（本题满分20分）已力1叭数*兀）=2cosx（cosx+/Jsinx）-1，-rgR.（1）求函数/（久）的单调递增区间;（2）设点儿（心$）屮2（心小〉，…止（盼儿），…都任函数y=/（x）的图象上,且满足心二石■凤■]7“=~2（«6N*）•求yl+y2+・・•+y2oi8的值.二、（本题满分20分）如图2•恻（:4x轴相切于点T（2.0）.y轴的正半轴相交于A出两点（月在8的上方）.且I佃I=3.⑴求圆C的方程;22（2）设过点b的r［线14椭畴+”1相交于p、q两点.求证:射线仙平分乙P4Q.三、（本题满分2（）分）如图3.在锐角AABC中川是RC的中点」州0过点AH.4直线BC相切T•点C.直线AM与闘O交「另一点D・H线BD与闘0交于另一点恳证明:ZEAC=乙BAC・\n四、(本题满分30分)L!知函数/(尤)=p^,g(x)=A(x-I).AeR.(1)证明:对任总AeR,山线y=g(x)都不nf能是曲线y=/(x)的切线；(2)杆ff任xe[e.e2_.使/(x)Wg)+\求k的取们范K五、(本题满分3()分)a(/+be)I)+c+1)("+ca)设a、b、c均为正实数,求证:G(C_+〃).,,+;三ab+be+ca.a+b\n2018年陕西省预赛答案一.选择錘（每小题6分.共&小题.共"分〉I.已知集合A/={x|a=sin(-：'巴w€zA.M£NB.M=N}-{4-TC.NC.W■=cos—.neZ>.则N的关系是（）D.Mp|N=0thB.易由周期性知M=N讯土"［}•1.已知a=log*5,b=Jog43.c=^.则a.kc*的大小关系呈()D.c>b>aA.a>b>cB.b>c>aCb>a>cthC・a=log2y/5>C.A=log2>1.c=；tan.r=-.94KI1626设x、ywR.且log4(x-^2y)+log4(x«2>)=L的最小值杲(甩石B・2C.2忑A.17Hl人由=4且*>2恻・不肪设x=2sec^/=tani9,ax-|v|=—--也凹.等式右边是〃的偶宙救.故不妨令J-呵,〃€[0,兰）n5in"+rcos〃=2.cos〃cos/?cos/?2.•.JF祈,诚〃+卩）=2=>话=〒^1=>尸23・故出且仅=b卜洽时取垠小值JT\nr若既约分政2(P，q征化为小数星….则当彳烟小时.P=()qA.9B.7C.5D.2D・由题就那(118<#<0.19q将罟-可見.陋若p增大・g的卜界不斷增大.=l时.不«在边长为&的正方IBCD中.MBC的中点.N&AD边上一点.且DN=3NA.若对于«ttm.在正方形ABCD的标上恰有b个不同的点P.ttP.Vf.p.V=m.则实敛加的取值范03罡()A.<-8,8)R(-1,24)C(78》D.(0,8)C.如图建泄宜爾坐杯系.・4(0・0),Af(&4),N(0、2).P(x.y).由88SW：：1,一—“：、PM•FN=(8-jr.4-y)・(-x.2-j)=x2+-6r+8=m,”*、］、!斗o(x-4F+(y-3)'=加+17•即以(4.3)为関心.@777为半權的蹄；••.与正方形四边右且仪fi6f不同的交点.易由用形対14<応帀<5=>加€(-1.0)・2…f%—：■■■■■二填空題(毎小雄8分.共4小題.共32分)9.设44BC的内角A.B.C所对的边分别为mg且4-C=^・0上疋成等差数列.Hcos^=th二2/>=2(cos2C-sin'C)=cosC+sinCncosC-sinC=-.3/•cosB=-cos(A+C)=-cos(2C+—)=sin2C=二.■4io如图.已知抛物线_r=2/zr(p>0)的焦点为F・准线为/・过点F的B[线与抛物线交于人〃两点.且|•呵“p・设点/<』在/上的射形为才・3'・今向四边形/M88内任投一点M・则点M落在"?TB'内的戡帝是.-1侑一冲卄一|"|・卩.网p_l3，几机“矽卜(|*才|+|8创)\A^(\A^\BF\)|,4E|.3p3II已知函&/(-v)=x+--l.若存在mX2.-sX.€[-^.4).佼得/CG+/(f…十/(・J)=/(l」，則正整x4n的最大值泉・4I119h6・由况慰御r(JT)=x+--lw卩，15—].故刃尽可(ft人时的情形为3+3+3+3+3-V5-・此时//=6.x44412设〃圧正楚故，当n>100^.石石的小舷棉分的前两位数解：因为Vn^+Sn+i-n-ia\n^+3n+i+n+l—Z=n又2100时，启+汁1-1+詐1+汁1+討*話詁故0.49<、n2+3n+l-n-l<0・5厕期小数部分前两位数为4并\n第二试一.(本小J8満分20分)已知函散fix)=2cosx(oosx.r)-hxc/?.(1)求函R/(x)的单调递增区阿；ffir⑵设点伽从斥(七亠).・・上(耳」讣…都a»tt^=/(x)的图喩上.且満足x产$..J-兀二亍求片令儿+…+，d的值.th(l>/(x)=cos2.r+>/3sin2x=2sin(2.r+—)•故/(x)的单调増区何为+阪三““keZ.636‘62•22,和A(*gZX・・>i+.比+…+).,口0・-2,n=2x二.(本小J8满分20分)如图，Hl-~)2=—.224⑵由QI)可知«0.4).8(0.1)・HSffcPp的斜率必“任・可设/y：F=b+l.卓命88等价于证明+设PgjJ.将自线方酬和阀方理联泄得(％口1疋十4&一6=0..•心讥严心十心=心+9“13・4“-3•主“斗x2.qx2xtx2-6三、(本小J8满分20分〉如图,在锐角“4BQ中.MSBC的中点・圆0过点.4且与J5线相切于点C\直线凡灯与DSO交于另一点D.直线BD与800交于另一点£・证明：ZEAC=ZBAC・由阀总定理如A创…・.&L=A/D膨L…SBC三MDM="DM="CE、又弦切他"CBmZAEC・SSlZ£^C-Za4C・if柝！四、(本小歴满分30分〉X已知函tt/(x)=—•g(x)=k(x-\lMR.lnx⑴证明：对任直民R.直线>=£(□<»不可能泉曲线y=/(A)的切线；⑵若存在xe[e.e2]t使/(x)^g(x)4-|.求*的取值范囤黑⑴呗金)的定义啊su(g・般设存在耳w(0・!)U(l・*c)使/⑴衽点(心・/(“)处的切伐方用为g(.Y)=A(N-l).WA=厂(心)=学匚斗・切线方幔为v=*-儿)+/(民2匕-勺二土+尹=&+丁—(呱)(Ing)Sx®(呱>对比时4盘严爲=盘严一呱平®此方旳^有-个实根z.\n此实根不在顒数的电文城内.故«1设不成立•证华!2(x-l)Inx2jf"，nX=A(x)・由A2/»").・xep.e2).12(x-l)lnx-(2—}-(2x-In*)(2In*+—-)h'(x)=；；X4(x-\Y(\nxyFiifVxe[e\e2],(x-l)ln.r-(2—)<(2x-lnxXlnx+xxo2(.r-l)ln.r--一ln.r<2xln.r+2A(.v-l)-(ln.r):--_Inx<=>-2lnx<2(jc-l)-(lnx)*.XXvlnx€(lv2]>/.(lnx)2-2lnxe|-L0],2(x-l)e[Ow2J.恳上h\x)<0-^/r((A:+cd)cfc'+亦)..设a〃.c>0・iE明：+*Xabtbc七gb^cc+aa^b证明：由对称性不妨设a>b^c>0j«J导乏辿之先傅F二仝z三，力2之肝NC2,b+cc*aa-»-bb*cc*aa^b三卄止汽亡b?+三八寿腆咅+乂+Wn若+竺+W从而a(a2+be)b(b2+ac)c(c2+ab)a3b3c3/abcabcabc\b+cc+aa+bb+cc+aa+b\b+cc+aa+b/ab2be2ca2abcabcabcb+cc+aa+bb+cc+aa+b当且仅当a=b=c时磚号成立，即原不蒔式成立.N:++r+:++r=ab+be+ca