【高中数学课件】实数与向量的积ppt课件 13页

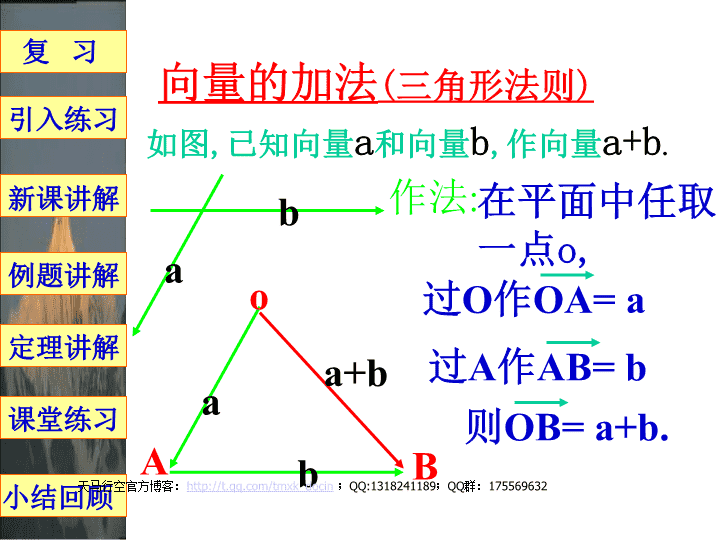
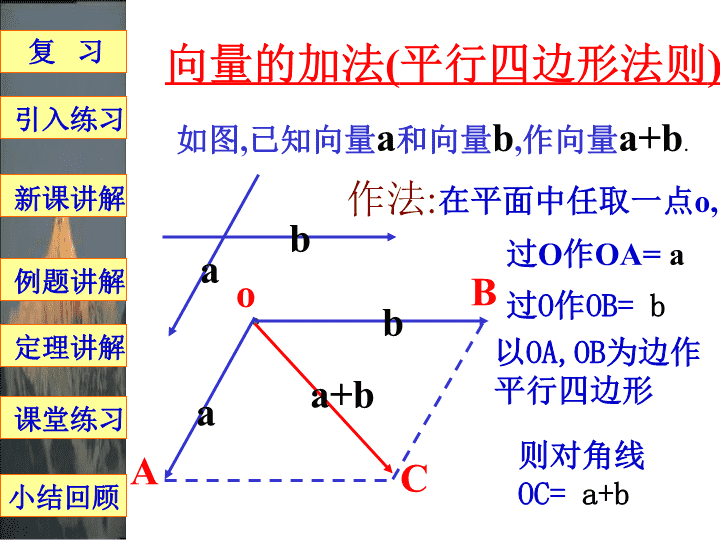
实数与向量的积第一课时主讲：郭兴刚天马行空官方博客：http://t.qq.com/tmxk_docin；QQ:1318241189；QQ群：175569632\n向量的加法(三角形法则)如图,已知向量a和向量b,作向量a+b.ab作法:在平面中任取一点o,aAbBa+b过O作OA=a则OB=a+b.过A作AB=bo复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习天马行空官方博客：http://t.qq.com/tmxk_docin；QQ:1318241189；QQ群：175569632\n向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.a作法:在平面中任取一点o,过O作OA=a过O作OB=boaAbBb以OA,OB为边作平行四边形则对角线OC=a+ba+bC复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习\n向量的减法(三角形法则）如图,已知向量a和向量b,作向量a-b.ab作法:在平面中任取一点o,过O作OA=a过O作OB=boaAbB则BA=a-ba-b复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习\n练习：试作出：a+a+a和(-a)+(-a)+(-a)已知非零向量a（如图）aaaa-a-a-aOABCPQMN相同向量相加以后，和的长度与方向有什么变化？复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习\n定义：一般地，实数λ与向量a的积是一个向量，记作λa，它的长度和方向规定如下：(1)|λa|=|λ||a|(2)当λ>0时,λa的方向与a方向相同；当λ<0时,λa的方向与a方向相反；特别地，当λ=0或a=0时,λa=0练习：课本P105-1,2(比较两个向量时,主要看它们的长度和方向)复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习\n(1)根据定义，求作向量3(2a)和(6a)(a为非零向量)，并进行比较。(2)已知向量a,b，求作向量2(a+b)和2a+2b，并进行比较。复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习=\n运算律：设a,b为任意向量，λ,μ为任意实数，则有：①λ(μa)=(λμ)a②(λ+μ)a=λa+μa③λ(a+b)=λa+λb例1计算：(1)(-3)×4a(2)3(a+b)–2(a-b)-a(3)(2a+3b-c)–(3a-2b+c)课本P105-3练习：答案：-12a5b-a+5b-2c复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习\n共线向量的充要条件：对于向量a(a≠0),b，以及实数λ,μ问题1：如果b=λa,那么，向量a与b是否共线？问题2：如果向量a与b共线那么，b=λa？定理：向量b与非零向量a共线的充要条件是有且只有一个实数λ，使得b=λa复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习\n例2如图，已知AD=3AB，DE=3BC，试判断AC与AE是否共线。课本P105-4定理：向量b与非零向量a共线的充要条件是有且只有一个实数λ，使得b=λa练习：复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习\n练习题：如图，在平行四边形ABCD中，点M是AB中点，点N在线段BD上，且有BN=BD，求证：M、N、C三点共线。复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习提示：设AB=aBC=b则MN=…=a+bMC=…=a+b\n小结回顾一、①λa的定义及运算律②向量共线定理(a≠0)b=λa向量a与b共线二、定理的应用：1.证明向量共线2.证明三点共线:AB=λBCA,B,C三点共线3.证明两直线平行:AB=λCDAB∥CDAB与CD不在同一直线上直线AB∥直线CD复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习\n作业布置：课本:第3题P108第4题第5题复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习