高中物理《力的分解》 教学 课件 新颖 39页

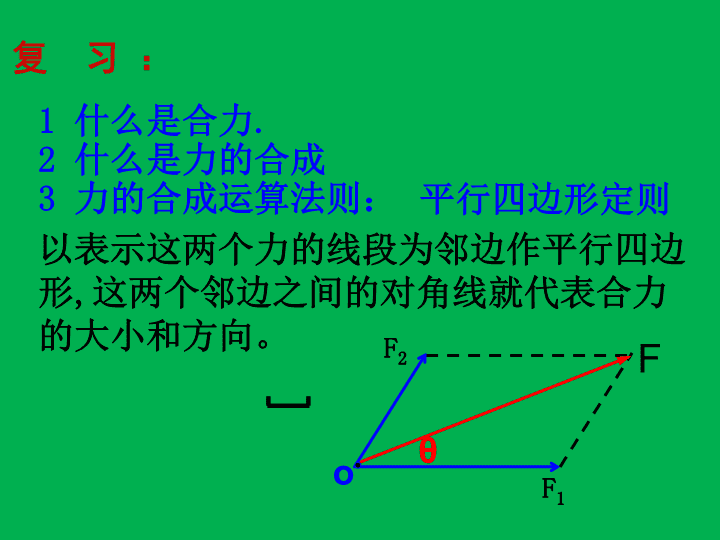
优质参赛课件主讲：****\n第三章相互作用力的分解\n1什么是合力.2什么是力的合成3力的合成运算法则：复习：以表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向。θF1F2oF平行四边形定则\n合力F分力F1和F2等效替代一、力的分解求一个已知力的分力的过程叫做力的分解。二、力的分解平行四边形定则力的分解是力的合成的逆运算合成分解\nF如果没有其它限制，对于同一条对角线，可以作出无数个不同的平行四边形．\n\nF2θFF1例1：放在水平地面上的物体受到一个斜向上方的拉力F的作用,F与水平方向成θ角,如图所示.怎样把力F分解?它的两个分力的大小、方向如何？按力所产生的实际作用效果进行分解\n能解决什么问题θGO·G1=GsinθG2=Gcosθ例2：把一个物体放在倾角为θ的斜面上，物体受到竖直向下的重力，应该怎样将重力分解？思考：随着斜面的倾角θ增大G1G2如何变化？\n\n练习光滑小球静止在斜面和挡板之间，小球所受的重力为G,求小球对挡板和斜面的压力。F1/G=tanαF1=GtanαG/F2=cosαF2=G/cosααGαF1F2\n例3.如图所示，悬挂物体的重力为G，杆重不计，绳子OA与杆OB的夹角为θ，求OA绳子和杆OB所受到的力OABθGG1G2θ\nF2F1GT1T2?(θ练习：在一根细线上用轻质挂钩悬挂一重为G的物体，挂钩与细线之间的摩擦忽略不计。已知细线所成的张角为θ，求细线的张力为多大？·OG/2F1θ/2(解:θ/2\n思考与讨论：在日常生活中有时会碰到这种情况：当载重卡车陷于泥坑中时，汽车驾驶员按图所示的方法，用钢索把载重卡车和大树栓紧，在钢索的中央用较小的垂直于钢索的侧向力就可以将载重卡车拉出泥坑，你能否用学过的知识对这一方法作出解释。F1F2FO·为什么四两可以拨千斤？\n斧思考与讨论为什么刀刃的夹角越小（刀刃越薄）越锋利？OF·\n如图所示，绳子MO与NO所能承受的最大拉力相同，长度MO>NO，则在不断增加重物G的重力过程中（绳OG不会被拉断）（）A、ON先被拉断B、OM先被拉断C、OM和ON同时被拉断D、无法确定哪条绳子先被拉断GOMNNGG1G2A\n合力F分力F1和F2合成分解等效替代一、力的分解求一个已知力的分力的过程叫做力的分解力的分解是力的合成的逆运算二.力的分解原则（按力所产生的实际作用效果进行分解）三、力的分解方法　平行四边形定则（矢量运算法则）课堂小结：\n什么是力的分解用几个分力来等效替代一个力1合力F分力F1和F2合成分解等效替代求一个力的分力叫做力的分解\n图甲GF2F1图甲的受力图图乙FF1F2图乙的受力图\n力的正交分解（1）力的正交分解法：把力沿着两个选定的互相垂直的方向分解，叫力的正交分解法。（2）正交分解的原理：一条直线上的两个或两个以上的力,其合力可由代数运算求得.当物体受到多个力作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便,为此建立一个直角坐标系,先将各力正交分解在两条互相垂直的坐标轴上,分别求出两个不同方向的合力Fx和Fy,然后可以由,求合力。\n一个物体受到四个力的作用，已知F1=1N，方向正东；F2=2N，方向东偏北600，F3=N，方向西偏北300；F4=4N，方向东偏南600，求物体所受的合力。F1F2F3F4xyF2xF2yF3yF3xF4xF4y600300600\nF1F2F3F4xyF2xF2yF3yF3xF4xF4y600300600\nFy=NFx=-1/2NF=1Nxy\n如图所示，电灯的重力为G，OA绳与顶板间的夹角为45度，0B绳子水平，则0A绳所受的拉力F1是多少？OB绳所受的拉力F2是多少？\n质量为m的木箱在拉力F的作用下，在水平地面上做匀速运动，如图所示，已知木箱与地面间的动摩擦因数为μ，那么物体受到的滑动摩擦力应为（）A.μmgB.μ(mg+Fsinθ)C.μ(mg-Ftanθ)D.FcosθθFD\n如图示，将质量分布均匀、重为G、半径为R的光滑圆球用长度也为2R的细绳拴在竖直墙壁上．要求得绳子对球的拉力FT和墙对球的支持力FN，通常有力的合成、力的分解和正交分解三种方法．请你：(1)画出这三种求解方法的力的示意图．在力的合成方法中，要说明合力是哪两个力的合力，在力的分解中，请对重力进行分解．(2)从三种方法中任选一种方法，解出绳子对球的拉力FT和墙对球的支持力F的大小．\n如图所示，重量为G的物体A，用与竖直线角α的力F推着靠在竖直的动摩擦因数为μ的墙壁上，若物体恰好能沿墙壁匀速下滑，求推力的大小。αGNFfα水平方向合力为零竖直方向合力为零\nF1氢气球重为10N，所受空气浮力为16N，由于受水平风力F作用，使系氢气球的绳子和地面成60度角，如图所示，求：（1）绳子的拉力F；（2）气球受到的水平风力F1。\n质量为m的物块，放在质量为M的斜面体上，如图所示。当在物块m上施加一个水平力F,且F由零逐渐加大到Fm的过程中，物块和斜面体仍保持静止状态。在此过程中，下列判断正确的是（）A.斜面体对物块m的支持力逐渐增大B.斜面体对物块m的支持力不变C.地面对斜面体的支持力逐渐增大D.地面对斜面体的支持力保持不变\n平行四边形定则F1F2FF1F2F三角形定则F1F2F或提示：一般情况下，矢量可以平移四、三角形定则\nABC把两个矢量首尾相接从而求出合矢量，这个方法叫做三角形定则。四、三角形定则矢量和标量：1．矢量：在物理学中，有大小,有方向,又遵守平行四边形定则的物理量叫做矢量．2．标量：在物理学中，只有大小、没有方向的物理量叫做标量．\n说一说一个物体的速度v1在一段时间内发生了变化,变成了v2,你能根据三角形定则找出变化量△v吗?v1v2△v\n如图所示，绳长AB=8m，轻杆BC=12m，墙上的两固定点AC=15m，所挂物体的重量G=60N。求绳受到的拉力与杆受到的压力。ABCGF1F2由力三角形BF1G和几何三角形ABC相似，则有：\n（1）已知一个力（合力）和两个力的方向，FOMNF1F2（2）已知合力的大小和方向，两个分力的大小3.力分解唯一性条件的讨论：两个分力的大小有惟一确定值，即可求得惟一的一对分力。\n（4）已知一个力(合力)和一个分力的方向,另一个分力有无数解，且具有最小值。OFF1F2（3）已知合力的大小和方向，另一个分力的大小和方向OFF2F1\n（4）已知合力F和分力F1的方向与分力F2的大小，可作如下讨论：（1）当θ<900时：①当F2F有惟一解，F2≤F无解\nF1的方向F1F2FθθF1F2FF1的方向F1F2FθF1'F2'②③④\n（5）已知合力和两个分力的大小。如已知合力F和两个分力大小分别为F1、F2，当F1+F2F时，有两解，如图所示，大小确定的F1和F2可构成两个三角形，一对分力中的F1与另一对分力中的F2大小相同，方向不同。F2F2F1F1FF\n2.已知合力和一个分力的大小和方向有唯一解三、有条件限制的力的分解：1.已知两分力的方向来分解力（力的方向按力所产生的实际作用效果来确定）有唯一解3.已知合力和两个分力的大小（F1+F2>F>F1-F2)4.已知合力F及一个分力的大小F2和另一个分力F1的方向Fθ①当F2F时,一组解\n再见！！