高中物理《单摆》课件 新人教版选修 51页

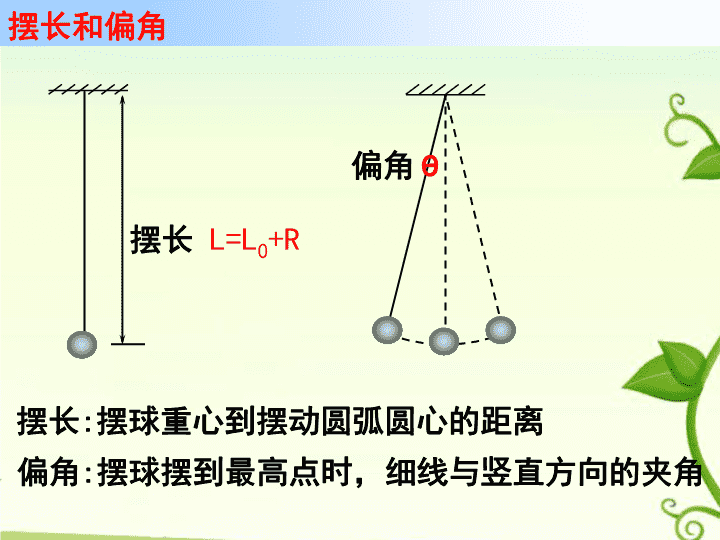
11.4《单摆》第一课时\n一、单摆1、在细线的一端拴一小球，另一端固定在悬点上，2、单摆是实际摆的理想化模型如果悬挂小球的细线的伸缩和质量可以忽略，线长又比球的直径大得多，这样的装置就叫做单摆。\n摆长L=L0+R摆长:摆球重心到摆动圆弧圆心的距离摆长和偏角θ偏角偏角:摆球摆到最高点时，细线与竖直方向的夹角\n演示实验\nCBAO1、回复力来源：重力沿切线方向的分力二、单摆的回复力F回=mgsinθθTGG2G1\n二、单摆的回复力当θ很小时，x≈弧长x位移方向与回复力方向相反sinθ≈θ=Lθ2、证明：TGG2G1F回=mgsinθ\n单摆振动的周期可能与哪些因素有关呢？三、单摆的周期\n三、单摆的周期实验一：单摆周期与振幅的关系\n三、单摆的周期实验二：单摆周期与摆球质量的关系\n三、单摆的周期实验三：单摆周期与摆长的关系\n三、单摆的周期结论4、与当地的重力加速度有关——重力加速度越大，周期越小单摆振动的周期1、与振幅无关——单摆的等时性2、与摆球的质量无关3、与摆长有关——摆长越长，周期越大\n单摆振动的周期公式：单摆做简谐运动的振动周期跟摆长的平方根成正比，跟重力加速度的平方根成反比。三、单摆的周期\n1、惠更斯利用摆的等时性发明了带摆的计时器.2、用单摆测定重力加速度。四、单摆周期公式的应用\n小结1、单摆模型2、单摆的回复力3、单摆的周期\n悬线：细、长、质量、伸缩可以忽略摆球：小而重（即密度大）1、用下列哪些材料能做成单摆()A.长为1米的细线B.长为1米的细铁丝C.长为0.2米的细丝线D.长为1米的麻绳E.直径为5厘米的泡沫塑料球F.直径为1厘米的钢球G.直径为1厘米的塑料球H.直径为5厘米的钢球A、F课堂练习\n2、单摆作简谐运动时的回复力是（）A.摆球的重力B.摆球重力沿圆弧切线的分力C.摆线的拉力D.摆球重力与摆线拉力的合力B课堂练习\n3、一个单摆，周期是T。a.如果摆球质量增到2倍，周期将；b.如果摆的振幅增到2倍，周期将；c.如果摆长增到2倍，周期将；d.如果将单摆从赤道移到北京，周期将；e.如果将单摆从海面移到高山，周期将；变小变大变大不变不变课堂练习\n思考与讨论小明家从广州搬到北京去,搬家时把家中的大摆钟也带到北京去了.问:1.这个摆钟到北京后是否还准时?2.若不准,是偏慢还是偏快?3.如须调整应该怎样调节?\n再见\n几种常见的摆圆槽摆钉摆圆锥摆\n如何理解单摆的周期公式5、如图为半径很大的光滑凹形槽，将有一小球从A点由静止释放。小球将做什么运动？θLO求运动的周期？A\n设光滑圆弧槽的半径为Ｒ，小球半径为r，摆角小于10°，求周期。圆槽摆\n6.一摆长为L的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是多少？课堂练习\n作业课后练习\n实验：研究用单摆测重力加速度11.4《单摆》第二课时\n得只要测出单摆的摆长L和振动周期T，就可以求出当地的重力加速度g的值，一、实验原理单摆做简谐运动时，其周期为：\n二、实验器材3、游标卡尺4、秒表（停表）1、单摆组2、米尺\n三、实验步骤1、做单摆：取约1米长的线绳栓位小钢球，然后固定在桌边的铁架台上。×\n二、实验步骤算出半径r，也准确到毫米2、测摆长：(1)用米尺量出悬线长L，准确到毫米(2)用游标卡尺测摆球直径摆长为L+rL051001\n二、实验步骤用秒表测量单摆的周期。3、测周期：把单摆从平衡位置拉开一个角度（＜5o）放开它\n2分7.6秒秒表的读数031233435637839411043121445164718492051225324265557285901267891011345121314\n0312334356378394110431214451647184920512253242655572859012678910113451213141分51.4秒秒表的读数\n二、实验步骤用秒表测量单摆完成30次全振动（或50次）所用的时间t，求出完成一次全振动所需要的时间，这个平均时间就是单摆的周期。3、测周期：把单摆从平衡位置拉开一个角度（＜5o）放开它T=t/n为了测量周期，摆球到达哪个位置的时刻作为计时开始与停止的时刻比较好？应以摆球经平衡位置计时开始与停止时刻\n二、实验步骤4、求重力加速度：把测得的周期和摆长的数值代入公式，求出重力加速度g的值来。改变摆长，重做几次实验.计算出每次实验的重力加速度.最后求出几次实验得到的重力加速度的平均值，即可看作本地区的重力加速度.5、多次测量求平均值：思考：如果要求用图象法来测定重力加速度，哪么应该如何建立坐标系？\n四、注意事项1、选择材料时应选择细轻又不易伸长的线，长度一般在1m左右，小球应选用密度较大的金属球，直径应较小，最好不超过2cm；2、单摆悬线的上端不可随意卷在铁夹的杆上，应夹紧在铁夹中，以免摆动时发生摆线下滑或悬点不固定，摆长改变的现象；3、注意摆动时摆角不易过大，不能超过10º，以保证单摆做简谐运动；4、摆球摆动时，要使之保持在同一个竖直平面内，不要形成圆锥摆；5、测量从球通过平衡位置时开始计时，因为在此位置摆球速度最大，易于分辨小球过此位置的时刻。6、为了减少偶然误差改变摆长，多次测量求平值。\n1、在做“用单摆测定重力加速度的实验”中为了减小误差，应注意的事项是()A．摆球以选密度大，体积小的小球为好;B．摆长以0.25米为宜;C．摆角应小于10°;D．摆线的悬点要固定，方不会在摆动中出现移动或晃动;E．要使单摆在竖直平面内摆动，不得使其形成锥形摆或摆球转动;F．测量周期时，应从摆球通过最低点时开始计时.①A、B、C、D项正确②只有E、F项正确③ACDEF正确④都正确③课堂练习\n2、某同学测定的g的数值比当地公认值大，造成的原因可能是()①摆球质量太大了；②量摆长时从悬点量到球的最下端；③摆角太大了（摆角仍小于10°）；④计算摆长时忘记把小球半径加进去；⑤计算周期时，将(n－1)次全振动误记为n次全振动.②⑤课堂练习\n3、为了提高实验精度，在试验中可改变几次摆长L，测出相应的周期Ｔ，从而得出一组对应的L与T的数值，再以L为横坐标Ｔ２为纵坐标，将所得数据连成直线如下图所示，则测得的重力加速度g=。1.04320.80.50l/mT2/s29.86m/s2课堂练习\n单摆的能量单摆作简谐运动时的动能和重力势能在发生相互转化，但机械能的总量保持不变，即机械能守恒。小球摆动到最高点时的重力势能最大，动能最小；平衡位置时的动能最大，重力势能最小。若取最低点为零势能点，小球摆动的机械能等于最高点时的重力势能，也等于平衡位置时的动能\n课堂练习4、小明家从广州搬到北京去,搬家时把家中的大摆钟也带到北京去了.问:1.这个摆钟到北京后是否还准时?2.若不准,是偏慢还是偏快?3.如须调整应该怎样调节?\n几种常见的摆圆槽摆钉摆圆锥摆\n如何理解单摆的周期公式5、如图为半径很大的光滑凹形槽，将有一小球从A点由静止释放。小球将做什么运动？θLO求运动的周期？A\n设光滑圆弧槽的半径为Ｒ，小球半径为r，摆角小于10°，求周期。圆槽摆\n6.一摆长为L的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是多少？课堂练习\n3．一物体在某行星表面受到的万有引力是它在地球表面受到的万有引力的1/4．在地球上走得很准的摆钟搬到此行星上后，此钟分针一整圈所经历的时间实际上是[]c\nc6．用空心铁球内部装满水做摆球，若球正下方有一小孔，水不断从孔中流出，从球内装满水到水流完为止的过程中，其振动周期的大小是[]A．不变B．变大C．先变大后变小回到原值D．先变小后变大回到原值\n15．将一摆长为L的单摆放置在升降机内，当升降机各以大小为a的加速度加速上升、减速上升时，单摆的周期各为多大？\nD9．一个单摆挂在电梯内，发现单摆的周期增大为原来的2倍，可见电梯在做加速度运动，加速度α为[]A．方向向上，大小为g/2B．方向向上，大小为3g/4C．方向向下，大小为g/4D．方向向下，大小为3g/4\n作业课后练习\n思考与讨论单摆振动是不是简谐运动？判断物体是否做简谐运动的方法：（2）根据回复力的规律F=-kx去判断（1）根据物体的振动图像去判断\n一般偏角θ<5°二、单摆的回复力结论在摆角很小的情况下，摆球所受的回复力跟位移大小成正比，方向始终指向平衡位置（即与位移方向相反），因此单摆做简谐运动