高中数学法向量ppt课件 39页

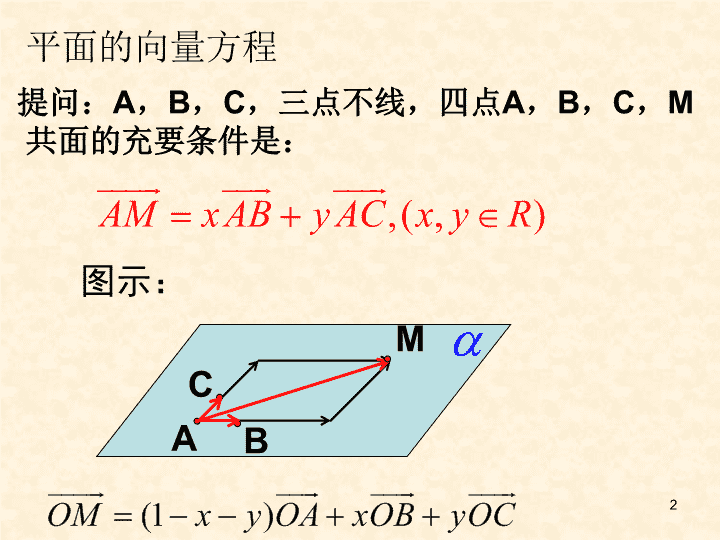
3.2.2平面的法向量与平面的向量表示1\n提问：A，B，C，三点不线，四点A，B，C，M共面的充要条件是：BACM图示：平面的向量方程2\n1.直线与平面垂直的定义2.平面的法向量：如果向量的基线与平面垂直，则向量叫平面的法向量。几点注意：1.法向量一定是非零向量;2.一个平面的所有法向量都互相平行;3.向量是平面的法向量，向量与平面平行或在平面内，则有3\nA给定一点A和一个向量,那么过点A,以向量为法向量的平面是完全确定的.l3.平面的向量表示：4\n因为方向向量与法向量可以确定直线和平面的位置，上节我们用直线的方向向量表示了空间直线、平面间的平行如何用平面的法向量表示空间两平面平行、垂直的位置关系呢？5\n4.两平面平行或重合、垂直的充要条件6\nl17\nl8\n9\n10\n11\n待定系数法12\n13\n例如图，已知矩形和矩形所在平面互相垂直，点分别在对角线上，且求证：ABCDEFxyzMN简证：因为矩形ABCD和矩形ADEF所在平面互相垂直，所以AB，AD，AF互相垂直。以为正交基底，建立如图所示空间坐标系，设AB,AD,AF长分别为3a，3b，3c，则可得各点坐标，从而有又平面CDE的一个法向量是因为MN不在平面CDE内所以MN//平面CDE14\n分析：要证明一条直线与一个平面垂直,由直线与平面垂直的定义可知,就是要证明这条直线与平面内的任意一条直线都垂直.例:(试用向量方法证明直线与平面垂直的判定定理)已知直线m,n是平面内的两条相交直线,如果⊥m,⊥n,求证:⊥.mng取已知平面内的任一条直线g,拿相关直线的方向向量来分析,看条件可以转化为向量的什么条件?要证的目标可以转化为向量的什么目标?怎样建立向量的条件与向量的目标的联系?15\nmng解:在内作不与m,n重合的任一直线g,在上取非零向量因m与n相交,故向量m,n不平行,由共面向量定理,存在唯一实数,使例:已知直线m,n是平面内的两条相交直线,如果⊥m,⊥n,求证:⊥.16\n6.有关平面的斜线概念，三垂线定理及其逆定理P10417\n什么叫平面的斜线、垂线、射影？如果aα,a⊥AO，思考a与PO的位置关系如何？∪aAPoαPO是平面α的斜线,O为斜足;PA是平面α的垂线,A为垂足;AO是PO在平面α内的射影.18\n例题分析：1、判定下列命题是否正确(1)若a是平面α的斜线、直线b垂直于a在平面α内的射影，则a⊥b。()(2)若a是平面α的斜线，b是平面α内的直线，且b垂直于a在β内的射影，则a⊥b。()××三垂线定理19\nPO平面PAO∪a⊥PO③答：a⊥PO三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。为什么呢？PA⊥αaα∪①PA⊥aAO⊥a②a⊥平面PAO三垂线定理PaAoα20\n1、三垂线定理描述的是PO(斜线)、AO(射影)、a(直线)之间的垂直关系。2、a与PO可以相交，也可以异面。3、三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。对三垂线定理的说明：三垂线定理4、三垂线定理的图形是由“四线一面”五个部件组成——垂线、斜线、射影、面内一线、平面21\n三垂线定理在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直。三垂线定理的逆定理：三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。PaAoα数式22\n另外,空间向量的运用还经常用来判定空间垂直关系,证两直线垂直线常可转化为证明以这两条线段对应的向量的数量积为零.23\n证明：如图,已知:求证：在直线l上取向量,只要证为24\n分析:逆定理同样可用向量,证明思路几乎一样,只不过其中的加法运算用减法运算来分析.25\n26\n27\n关于三垂线定的应用，关键是找出平面(基准面)及垂线。至于射影则是由垂足、斜足来确定的，因而是第二位的。第一、定平面(基准面)第二、找平面垂线（电线杆）第三、看斜线，射影可见三垂线定理第四、证明直线a垂直于射影线，从而得出a与b垂直。强调：1°四线是相对同一个平面而言。2°定理的关键是找“基准面”和“电线杆”。28\nA1D1C1B1ACBDFE29\n证明:设正方体的棱长为1,建立如图的空间直角坐标系xyzA1D1C1B1ACBDFE30\nABCO31\n小结1.直线与平面垂直的定义2.平面的法向量：3.平面的向量表示：4.两平面平行或重合、垂直的充要条件6.有关平面的斜线概念，三垂线定理及其逆定理P10432\n巩固性训练11.设分别是直线l1,l2的方向向量,根据下列条件,判断l1,l2的位置关系.平行垂直平行33\n巩固性训练21.设分别是平面α,β的法向量,根据下列条件,判断α,β的位置关系.垂直平行相交34\n1、设平面的法向量为(1,2,-2),平面的法向量为(-2,-4,k),若，则k=；若则k=。2、已知，且的方向向量为(2,m,1)，平面的法向量为(1,1/2,2),则m=.3、若的方向向量为(2,1,m),平面的法向量为(1,1/2,2),且，则m=.巩固性训练335\n36\n1．如图，正方体中，E为的中点，证明：//平面AEC练习:用空间向量来解决下列题目2、在正方体AC中，E、F、G、P、Q、R分别是所在棱AB、BC、BBAD、DC、DD的中点，求证：⑴平面PQR∥平面EFG。⑵BD⊥平面EFGABCDABCDFQEGRP37\n例.在空间直角坐标系内，设平面经过点，平面的法向量为，为平面内任意一点，求满足的关系式。解：由题意可得38\n此课件下载可自行编辑修改，供参考！感谢您的支持，我们努力做得更好！