高中数学算法初步课件59张 59页

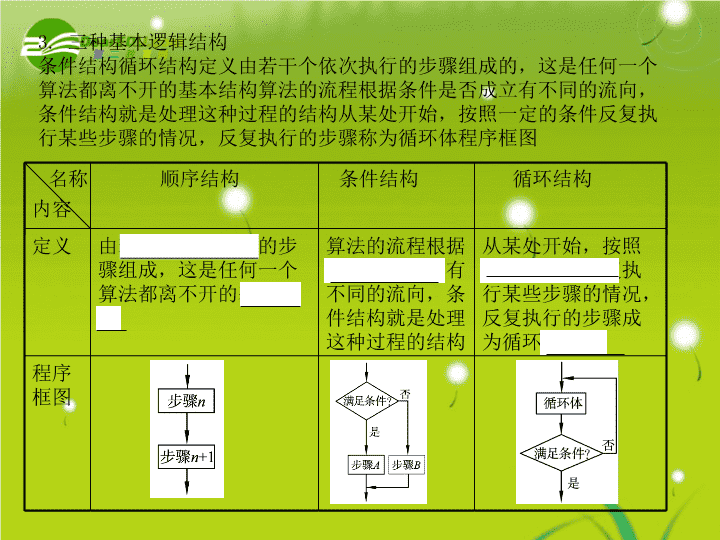
学科网之数学直通车----算法初步知识体系\n第一节算法与程序框图基础梳理1.算法通常是指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是确定的和能执行的，而且能够在有限步之内完成.2.程序框图（1）定义：程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形.（2）说明：在程序框图中，一个或几个程序框的组合表示算法中的一个步骤；带有方向箭头的流程线将程序框连接起来，表示算法步骤的执行顺序.\n3.三种基本逻辑结构条件结构循环结构定义由若干个依次执行的步骤组成的，这是任何一个算法都离不开的基本结构算法的流程根据条件是否成立有不同的流向，条件结构就是处理这种过程的结构从某处开始，按照一定的条件反复执行某些步骤的情况，反复执行的步骤称为循环体程序框图名称顺序结构条件结构循环结构内容定义由若干个依次执行的步骤组成，这是任何一个算法都离不开的基本结构算法的流程根据条件是否成立有不同的流向，条件结构就是处理这种过程的结构从某处开始，按照一定的条件反复执行某些步骤的情况，反复执行的步骤成为循环体程序框图\n典例分析题型一算法的设计【例1】已知点和直线l:Ax+By+C=0（A≠0），求点到直线l的距离d，写出其算法并画出程序框图.分析由公式可知，欲求点到直线的距离，要先求及，代入，用顺序结构解决.解算法如下：第一步，输入点P的坐标x0,y0及直线方程的系数A、B、C.第二步，计算第三步，计算第四步，计算第五步，输出d.\n程序框图:学后反思给出一个问题，设计算法时应注意：（1）认真分析问题，联系解决此问题的一般数学方法；（2）综合考虑此类问题中可能涉及的各种情况;（3）将解决问题的过程划分为若干个步骤；（4）借助变量或参数用数学表达式表述算法；（5）用简练的语言将各个步骤表示出来.\n１城区一中学生数学模块学分认定由模块成绩决定，模块成绩由模块考试成绩和平时成绩构成，各占50%，若模块成绩大于或等于60分，获得2学分，否则不能获得学分（为0分），设计一算法，通过考试成绩和平时成绩计算学分，并画出程序框图开始结束输入a,bS>=60?credit=2credit=0否是S=(a+b)*0.5输出credit\n２、对任意正整数n,的值,并画出程序框图.开始输入一个正整数n输入S的值结束S=0i=1S=S+1/ii=i+1i≤nYN设计一个算法求步骤A步骤B思考:将步骤A和步骤B交换位置，结果会怎样？能达到预期结果吗？为什么？要达到预期结果，还需要做怎样的修改？\n例3设计一算法，求和:1+2+3+…+100结束i=i+1Sum=Sum+ii<100?输出Sum否是i=0，Sum=0开始结束输出Sumi=0，Sum=0开始i=i+1Sum=Sum+ii>=100?否是能否说说这个流程图的异同点？\ni=i+1Sum=Sum+i解决方法就是加上一个判断，判断是否已经加到了100，如果加到了则退出，否则继续加。直到型结构当型结构i=i+1Sum=Sum+i是否i=i+1Sum=Sum+i否是i<100?i>=100?请填上判断的条件。\n开始输入aa≥0输出|a|=a输出|a|=-a结束NYＰ１１　练习１\n开始X1=1X2=2m=(x1+x2)/2x2=mx1=mm*m－3<>0|x1－x2|＜0.005(x1*x1－3)*(m*m－3)＞0输出所求的近似值m结束m=(x1+x2)/2NyyN练习２\n▲下面是关于城市居民生活用水收费的问题为了加强居民的节水意识，某市制定了以下生活用水收费标准：每户每月用水未超过７ｍ３时，每立方米收费1.0元，并加收0.2元的城市污水处理费,超过７ｍ３的部分,每立方米收费1.5元，并加收0.4元的城市污水处理费.开始输入xx≤7y=1.2xy=1.9x－4.9输入y结束yNP.11习题A组第1题程序框图\n开始S=0I=I+1I=1S=S+I*II≤100输出S结束NYP.11习题1.1A组第2题\n输入x开始x＞3y=1.2x+1.4y=5输入y结束NYP.11习题A组第3题程序框图\n开始输入50米跑成绩:xx＜6.8输出提示“若要继续请按键”Y“，否则请按其他键输入到变量mm=“y”orm=“Y”结束输出xNYYNP.11习题1.1B组第1题程序框图\n开始输出提出：“输入第一个方程的系数”“x的系数是”：a1“y的系数是”：b1“常数项是”：c1输出“x=”;x“y=”;y方程有无数多组解a1*b2－a2*b1≠0x=(c2*b1－c1*b2)/(a1*b2－a2*b1)y=(c2*b1－c1*b2)/(a1*b2－a2*b1)结束输出提出：“输入第二个方程的系数”“x的系数是”：a2“y的系数是”：b2“常数项是”：c2NYc1=c2方程无解P.11习题1.1B组第2题\n举一反三1.写出求解方程a+x+c=0的一个算法.解析第一步，判断a是否等于零.若a=0，则解x=-c;若a≠0，则执行第二步.第二步，判断判别式Δ=1-4ac是否小于零.若Δ<0，则原方程无实数解；若Δ≥0，则执行第三步.第三步，计算第四步，输出方程的实数解.\n题型二算法的顺序结构【例2】如图，设计算法求底面边长为4，侧棱长为5的正四棱锥的侧面积及体积，并画出相应的程序框图.分析方法一：先求体积V=Sh,S=,高h=，R=a,斜高h′=，从而求得=4×ah′=2ah′.方法二：推导出利用a和l表达的侧面积及体积公式，然后代入求解.\n解由方法一可得算法一：第一步,a=4,l=5.第二步,R=a.第三步,h=,S=.第四步,V=Sh.第五步,输出V.第六步,h′=.第七步,=2ah′.第八步,输出.由方法二得算法二:第一步,a=4,l=5.第二步,S侧=2a.第三步,V=第四步,输出S侧、V.\n算法一程序框图如图1，算法二程序框图如图2.图1图2\n学后反思通过本题体会算法的思想，比较两种算法的优点.利用算法和程序框图，能够规范思维，可以锻炼书面表达的能力，先求什么，后求什么，无论是用算法表达，还是用程序框图表达，都是一目了然，非常清晰的，所以把这种方法用于我们平时的做题会使解题的思路简练、易懂、有逻辑性.2.写出求过两点（2,0),(0,3)的直线方程的一个算法，并画出程序框图.解析算法如下：第一步，a=2,b=3.第二步，输出结果程序框图：\n题型三算法的条件结构【例3】“特快专递”是目前人们经常使用的异地邮寄信函或托运物品的一种快捷方式，某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算：f=0.53ω(ω≤50),50×0.53+(ω-50)×0.85(ω>50).其中f（单位：元）为托运费，ω为托运物品的重量（单位：kg）.试设计计算费用f的算法，并画出程序框图.分析这是一个实际问题，求费用f的计算公式随物品的重量ω的变化而不同，因此要对物品重量ω进行判断，比较ω与50的大小，然后由相应关系式求出费用f并输出.\n解算法如下：第一步，输入ω.第二步，如果ω≤50,那么f=0.53ω；否则，f=50×0.53+(ω-50)×0.85.第三步，输出f.程序框图：学后反思利用条件结构解决算法问题时，要引入判断框，要根据题目的要求引入一个或多个判断框，而判断框内的条件不同，对应的下一图框中的内容和操作要相应地进行变化，故要逐个分析判断框内的条件.\n3.儿童乘坐火车时，若身高不超过1.1m，则无需购票;若身高超过1.1m，但不超过1.5m，可买半票;若超过1.5m，应买全票.请以此设计一个算法并画出相应的程序框图.解析算法如下：第一步,测量儿童身高h.第二步,如果h≤1.1,那么免费乘车;否则，如果h≤1.5，那么买半票乘车;否则买全票.程序框图如图所示.举一反三\n题型四算法的循环结构【例4】(12分)某企业2008年的生产总值为200万元，技术创新后预计以后每年的生产总值将比上一年增加5%，问:最早哪一年的生产总值将超过300万元？试写出解决该问题的一个算法，并画出相应的程序框图.分析设第n年后该企业生产总值为a,则,此时为(2008+n)年.解算法设计如下：第一步，n=0,a=200,r=0.05.第二步，T=ar（计算年增量）.第三步，a=a+T（计算年产量）…………………………….3′第四步，如果a≤300,那么n=n+1，重复执行第二步;如果a>300，则执行第五步.第五步，N=2008+n.第六步，输出N……………………………………………6′\n程序框图：方法一：方法二：……………12′…………12′\n学后反思注意直到型循环结构和当型循环结构的本质区别，直到型循环结构先执行a=a+T，再判断a>300，若不满足，则执行循环体，直到满足才输出N；而当型循环结构先判断a≤300，若成立，则执行循环体，直到a≤300不成立才结束循环，输出N.举一反三4.（2009·江苏）如图是一个算法的流程图，最后输出的W=.答案:22解析:第一次：T=1,S=1-0=1;第二次：T=3，S=3-1=8；第三次：T=5，S=5-8=17，此时满足S≥10,所以W=S+T=17+5=22.\n易错警示【例1】设计一个程序框图，求的值.错解如图1，图2.\n错解分析图1的错误在于i=i+1，步长为1，计算的是图2的错误在于先执行i=i+2而后执行，计算的是正解\n【例2】已知函数请设计一个程序框图求函数值y.错解程序框图如图1，图2.图1图2\n错解分析图1表示的函数为故错误.图2的错误在于被判断的条件x=0放在菱形框外，应放在菱形框里，同时菱形判断框只能有一个进口和两个出口.正解程序框图如图.\n考点演练答案:A>0？V=S+T10.（2009·辽宁改编）某店一个月的收入和支出总共记录了N个数据，其中收入记为正数，支出记为负数.该店用如图所示的程序框图计算月总收入S和月净盈利V，那么在图中空白的判断框和处理框中，应分别填入，.解析:分析题意并结合框图可知：S代表收入，T代表支出，∴当A=>0时，累加到S，反之，累加到T，故判断条件为A>0?;则知T<0，∴总利润V=S+T.\n第10题图\n11.用代表第i个学生的学号，代表第i个学生的成绩(i=1,2,3,…,50).设计程序框图打印出不低于80分的全部学生的学号和成绩.解析\n12.在国家法定工作日内，每周满工作量的时间为40小时，若每周工作时间不超过40小时，则每小时工资8元；如因需要加班，超过40小时的每小时工资为10元.某公务员在一周内工作时间为x小时，但他须交纳个人住房公积金和失业保险（这两项费用为每周总收入的10%）.试分析算法步骤并画出其净得工资y元的算法的程序框图.(注：满工作量外的工作时间为加班）解析算法如下：第一步，输入工作时间x小时.第二步，若x≤40，则y=8x×(1-10%)；否则，y=40×8(1-10%)+(x-40)×10(1-10%).第三步，输出y值.程序框图：\n\n第二节基本算法语句1.三种语句的一般格式和功能语句一般格式功能输入语句输出语句赋值语句INPUT“提示内容”；变量输入信息PRINT“提示内容”；表达式输出结果变量=表达式将表达式的值赋给变量2.条件语句（1）定义：算法中的由条件语句来表达.（2）条件语句的格式及框图①IF—THEN格式条件结构基础梳理\n②IF—THEN—ELSE格式3.循环语句（1）算法中的循环结构是由循环语句来实现的.（2）循环语句的格式及框图.①UNTIL语句\n②WHILE语句（3）WHILE语句和UNTIL语句之间的区别与联系WHILE语句UNTIL语句区别执行循环体前测试条件，当条件为真时执行循环体，当条件为假时终止循环，可能不执行循环体执行循环体后测试条件，当条件为假时执行循环体，当条件为真时终止循环，最少执行一次循环体联系可以相互转换，LOOPUNTIL(条件)相当于WHILE（反条件）\n题型一输入、输出和赋值语句【例1】某企业为职工计算工资时按时间计，每月的总工资=每月劳动时间×每小时工资，从总工资中扣除15%作为医疗保险金，再以总工资的5‰作为奖金，要求输入劳动时间和每小时工资数，输出每位职工应发工资.设计算法并画出程序框图，写出程序.分析（1）设出每小时工资，每月劳动时间，每月总工资，先求出每月总工资，再求应发工资.（2）在程序编写中赋值语句是其中关键的基本语句.解算法如下：第一步，输入月劳动时间t和每小时工资a.第二步，求每月总工资y=每月劳动时间t×每小时工资a.第三步，求应发工资z=每月总工资y×(1-15%)+y×5‰.第四步，输出应发工资z.典例分析\n程序框图：程序：INPUTt,ay=a*tz=0.855*yPRINTzEND学后反思编写程序的关键是先搞清问题的算法，特别是算法的结构，然后确定采用哪一种算法语句.本题实质是求一个函数对应于自变量的函数值，故可用顺序结构实现算法.\n举一反三1.(2009·临沂模拟）下列赋值语句中正确的有（）①3=B;②x-y=2;③A=B=-2;④T=T+T.A.0个B.1个C.2个D.3个解析：①错，赋值语句中变量不能给常数赋值;②错，赋值语句不能给一个表达式赋值;③错，赋值语句只能给一个变量赋值；④正确.答案：B\n题型二条件语句【例2】如图，已知底角45°的等腰梯形ABCD，底边BC长为7cm，腰长为22cm，当一条垂直于底边BC（垂足为F）的直线l从B点开始由左至右移动（与梯形ABCD有公共点）时，直线l把梯形分成两部分，令BF=x(0≤x≤7)，左边部分的面积为y，求y与x之间的函数关系式，并画出程序框图，写出程序.分析因为面积y随着x的增大是求不同图形的面积和，所以要用分段函数求y与x之间的函数关系式，然后在此基础上画出程序框图，写出程序.解过点A、D分别作AG⊥BC，DH⊥BC，垂足分别是G、H.∵四边形ABCD是等腰梯形，底角是45,AB=22cm，∴BG=AG=DH=HC=2cm.又BC=7cm,∴AD=GH=3cm,所以\n程序框图:程序一：INPUT“x=”;xIFx>=0ANDx<=2THENy=0.5*x*xELSEIFx<=5THENy=2*x-2ELSEy=-0.5*(x-7)∧2+10ENDIFENDIFPRINTyEND\n程序二：INPUT“x=”;xIFx>=0ANDx<=2THENy=0.5*x*xENDIFIFx>2ANDx<=5THENy=2*x-2ENDIFIFx>5ANDx<=7THENy=-0.5*(x-7)∧2+10ENDIFPRINTyEND学后反思条件语句一般用在需要对条件进行判断的算法设计中.在求分段函数的函数值时，由于自变量x的值不同，其函数值的求法也不同，故先对x的值进行判断，然后根据其具体值选择不同的计算方法，故用条件语句进行算法设计.\n举一反三2.到银行办理个人异地汇款（不超过100万）时，银行要收取一定的手续费，汇款额不超过100元，收取1元手续费；超过100元但不超过5000元，按汇款额的1%收取；超过5000元，一律收取50元手续费.试用条件语句描述汇款额为x元时，银行收取手续费为y元的过程，画出程序框图并写出程序.解析：依题意，手续费y与汇款额x之间的关系式为（单位：元）程序框图：\n程序：INPUT“汇款金额为”；xIFx>0ANDx<=100THENy=1ELSEIFx<=5000THENy=0.01*xELSEy=50ENDIFENDIFPRINT“手续费为”;yEND\n题型三循环语句【例3】(2010·青岛模拟)2008年9月发生了“三鹿奶粉污染”事件，主要是在一些企业生产的奶制品中检测出含三聚氰胺，三聚氰胺是一种有毒的化工原料，俗称“假蛋白”.蛋白质主要由氨基酸组成，蛋白质平均含氮量为16%左右，而三聚氰胺的含氮量为66%左右，不法分子往往在奶制品中加三聚氰胺主要是因为它能冒充蛋白质.2008年9月16日国家质检总局公布了22家企业生产的婴幼儿配方奶粉中含有三聚氰胺，其中最高含量为2563mg/kg,最低含量为0.09mg/kg.设计一个求含量高于20mg/kg的婴幼儿配方奶粉的平均含量的程序框图，并写出程序.分析（1）由于涉及到22家企业，因此使用循环结构来控制企业数；（2）用条件结构来判断含量是否高于20，同时统计高于20mg/kg的总和与企业数.\n学后反思在解决实际问题时，要正确理解其中的算法思想，根据题目写出其关系式，再写出相应的算法.在循环语句中，也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套这些语句需要保证语句的完整性，否则就会造成程序无法执行.解程序框图：程序：S=0M=0i=1DOINPUTxIFx>20THENS=S+xM=M+1ENDIFi=i+1LOOPUNTILi>22P=S/MPRINTPEND\n举一反三3.高一(1)班共60人,市青少年保护中心来抽样检测同学们的身体素质,要求学号能被3整除的同学参加体检,已知学生的学号从1到60号.请画出输出参加同学学号的程序框图，并编写程序解析：程序框图如图所示:程序如下:S=0WHILES<60S=S+3PRINTSWENDEND\n题型四算法语句的实际应用【例4】(12分)青年歌手电视大奖赛共有10名选手参加,并请了12名评委,在计算每位选手的平均分数时,为了避免个别评委所给的极端分数的影响,必须去掉一个最高分和一个最低分后再求平均分数.试设计一个算法解决该问题，要求画出程序框图，写出程序（假定分数采用10分制，即每位选手的分数最低为0分，最高为10分）.分析此题难度较大，利用循环结构，而循环结构中还有条件结构，要分清层次.最好先写算法分析再画程序框图，最后写出程序解算法分析：由于共有12名评委，所以每位选手会有12个分数，我们可以用循环结构来完成这12个分数的输入，同时设计累加变量求出这12个分数之和.本题的关键在于从这12个输入的分数中找出最大数与最小数，以便从总分中减去这两个数.由于每位选手的分数都介于0分和10分之间，故我们可以先假设其中的最大数为0，最小数为10，然后每输入一个评委的分数，就进行一次比较.若输入的数大于0，就将其代替最大数；若输入的数小于10，就用它代替最小的数；依次比较下去，就能找出这12个数中的最大数与最小数，循环结束后，从总和中减去最大数与最小数，再除以10，就得到该选手最后的平均分数.\n学后反思在解决实际问题时，要正确地理解其中的算法思想，根据题目写出其关系式，再写出相应的算法步骤，画出程序框图，最后准确地编写出程序，要注意总结算法、程序框图、程序三者之间的关系.程序框图:程序如下：S=0k=1max=0min=10DOINPUTxS=S+xIFmax<=xTHENmax=xENDIFIFmin>=xTHENmin=xENDIFk=k+1LOOPUNTILk>12S1=S-max-mina=S1/10PRINTaEND………………………12′……………6′\n举一反三4.用分期付款的方式购买价格为1150元的冰箱，如果购买时先付150元，以后每月付50元，再加上欠款的利息.若一个月后付第一个月的分期付款，月利率为1%，那么购买冰箱的钱全部付清后，实际共付出款额多少元？画出程序框图，写出程序.解析：购买时付款150元，余款1000元分20次付清，每次的付款数组成一个数列{},=50+(1150-150)×1%=60,=50+(1150-150-50)×1%=59.5,……=50+［1150-150-(n-1)×50］×1%=60-(n-1)(n=1，2，3，…，20),∴=60-×19=50.5.总和S=150+60+59.5+…+50.5.\n程序框图：程序如下：a=150m=60S=0S=S+ai=1WHILEi<=20S=S+mm=m-0.5i=i+1WENDPRINTSEND\n【例】已知分段函数编写程序，输入自变量的值，输出其对应的函数值y.错解程序如下：INPUTxIFx<0THENy=-x+1ELSEIFx=0THENy=0ELSEy=x+1ENDIFEND错解分析(1)每个IF都必须有一个ENDIF与之匹配；(2)错解无输出语句.易错警示\n程序如下：INPUTxIFx<0THENy=-x+1ELSEIFx=0THENy=0ELSEy=x+1ENDIFENDIFPRINTyEND正解\n10.（2009·东营模拟）下面程序运行后输出的结果为.x=5y=-20IFx<0THENx=y-3ELSEy=y+3ENDIFPRINTx-y,y-xEND解析：x=5，不满足条件x＜0，则执行y=y+3,即y=-17,故x-y=5-(-17)=22,y-x=-17-5=-22.答案：22,-22考点演练\n11.元旦期间，某商场搞挂历促销活动：原价每本20元，购买5到9本按9折收费，购买10本或10本以上按8折收费，画出收费的程序框图，并写出相应的程序.解析：程序框图：程序：INPUT“x=”；xIFx＜5THENy=20*xELSEIFx＞=10THENy=20*0.8*xELSEy=20*0.9*xENDIFENDIFPRINTyEND\n12.2008年某地森林面积为1000，且每年增长5%，到哪一年该地森林面积超过2000.请设计一个程序，并画出程序框图.解析：需要一个累加变量和一个计数变量，将累加变量的初值设为1000，计数变量从0开始取值.程序框图：程序：P=1000N=0DOP=P*(1+0.05)N=N+1LOOPUNTILP＞2000N=2008+NPRINTNEND