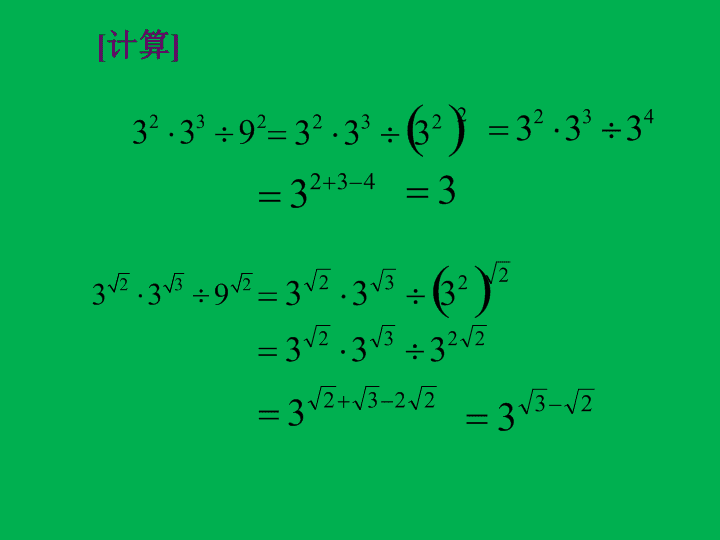高中数学参赛课件 指数函数 13页

指数函数学习目的:掌握指数函数的概念,图像,性质,并学会其简单的应用重点和难点:指数函数的图像和性质\n[计算１]有理指数幂１,1.4,1.41,1.414,1.4142,…4.656,4.707,4.728,4.729,3,…指数从有理数推广到实数无理指数幂实数指数幂\n[计算]\n引例：１、某种细胞分裂时，由1个分裂成2个,2个分裂成4个……1个这样的细胞分裂x次后，得到的细胞个数y与x的函数关系式是什么?\n2、某工厂从今年起年产值每年比上一年增长6%，设去年年产值为单位1，经过x年后产值为y,那么该工厂年产值y关于年份x的函数解析式为去年今年第１年年产值第２年第３年第０年\n一、定义1、指数函数的定义：函数其中x是自变量，函数定义域是R。2、定义的理解２）规定a>0,且a≠１３）y=ax中,ax系数是1，只有１项1）定义域是R对底数a(常数)有三个限制——非零、非负、非1辨析\n０xy０xy2指数函数的图像及其特征\n(1)定义域：R(2)值域：(0,+)(3)过点(0,1),即x=0时y=1(５)x>0时，y>1x<0时,00时,013指数函数的图像和性质Y=ax图像性质a>101∴y=1.7x在R上是增函数∵2.5<3,∴1.72.5<1.73\n（2）考虑函数y=0.8x∵0.8<1∴y=0.8x在R上是减函数∵-0.1>-0.2,∴0.8-0.1<0.8-0.2(2)0．8-0.1，0．8-0.2(3)1.70.3，0.93.1(3)∵1.70.3>1,0.93.1<1∴1.70.3>0.93.1\n小结：1指数函数的概念2指数函数的图像和性质3指数函数的性质的应用4数学思想和方法分类讨论由特殊到一般数形结合\n家庭作业课本　　　　１１０页　　第１、２题《基础与发展》１１１－１１２页基础性检测题（Ａ）一张薄纸，第一次，将它对折成两层；第二次将它对折成四层……假设对折20次，请问我们它的厚度能超过教室的高度吗？（50张的厚度为5mm）想一想\n①若a=0无意义。当x≤0时，为了避免上述各种情况，所以规定a>0且a1。②若a<0，则对于x的某些数值，可使无意义。如，这时对于x=，x=……等等，在实数范围内函数值不存在.③若a=1，则对于任何xR，=1，是一个常量，没有研究的必要性.