- 1.84 MB
- 2022-08-05 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
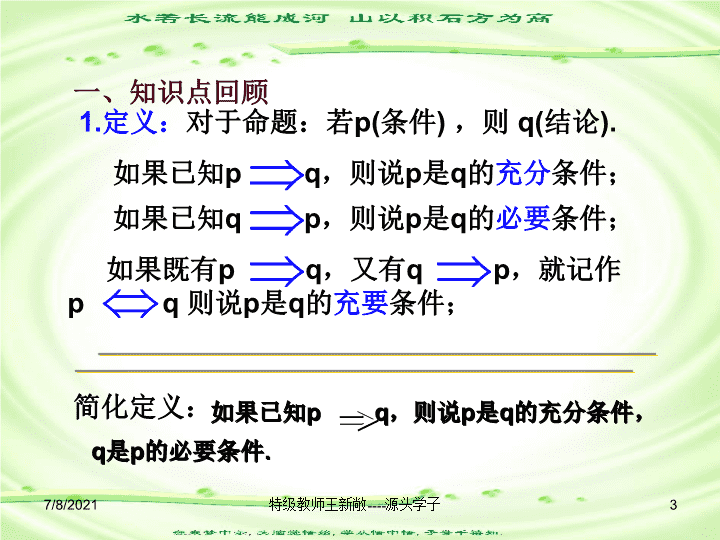
高中数学复习专题讲座人教版高中数学高考复习专题讲座充要条件的理解及判定方法主讲:特级教师王新敞\n教学目的:教学重点:教学难点:1.掌握充分条件、必要条件的意义及判定.2.培养学生的逻辑推理能力.充分条件、必要条件的判断充分条件、必要条件的判断方法及证明格式.7/8/20212特级教师王新敞----源头学子\n1.定义:对于命题:若p(条件),则q(结论).如果已知pq,则说p是q的充分条件;如果既有pq,又有qp,就记作pq则说p是q的充要条件;如果已知qp,则说p是q的必要条件;简化定义:如果已知pq,则说p是q的充分条件,q是p的必要条件.一、知识点回顾7/8/20213特级教师王新敞----源头学子\n①pq,相当于PQ,即PQ或P、Q②qp,相当于QP,即QP或P、Q③pq,相当于P=Q,即P、Q有它就行缺它不行同一事物2.从集合角度理解以上的定义:一、知识点回顾7/8/20214特级教师王新敞----源头学子\n3.三种条件的理解,可以通过下列电路图来说明AB①DC②E③①A、B仅充分②C、D仅必要③E充要对于电路通一、知识点回顾7/8/20215特级教师王新敞----源头学子\n①认清条件和结论。②考察pq和qp的真假。4.判别步骤:①在句型:A是B的?条件中,A是条件,B是结论.②在句型:A的?条件是B中,B是条件,A是结论.注意:①可先简化命题.③将命题转化为等价的逆否命题后再判断.②否定一个命题只要举出一个反例即可.5.判别技巧:一、知识点回顾7/8/20216特级教师王新敞----源头学子\n例1有A、B、C三个盒子,其中一个内放有一个苹果,在三个盒子上各有一张纸条.A盒子上的纸条写的是“苹果在此盒内”,B盒子上的纸条写的是“苹果不在此盒内”,C盒子上的纸条写的是“苹果不在A盒内”.如果三张纸条中只有一张写的是真的,请问苹果究竟在哪个盒子里?苹果在AAAB苹果在BBCC苹果在C分析:真真真真真假假假假二、重难点讲解A苹果在BC7/8/20217特级教师王新敞----源头学子\n例1有A、B、C三个盒子,其中一个内放有一个苹果,在三个盒子上各有一张纸条.A盒子上的纸条写的是“苹果在此盒内”,B盒子上的纸条写的是“苹果不在此盒内”,C盒子上的纸条写的是“苹果不在A盒内”.如果三张纸条中只有一张写的是真的,请问苹果究竟在哪个盒子里?解:若苹果在A盒内,则A、B两个盒子上的纸条写的为真,不合题意;若苹果在B盒内,则A、B两个盒子上的纸条写的为假,C盒子上的纸条写的为真,符合题意,即苹果在B盒内;若苹果在C盒内,则B、C两盒子上的纸条写的为真,不合题意.综上,苹果在B盒内.二、重难点讲解7/8/20218特级教师王新敞----源头学子\n二、重难点讲解例2已知p、q都是r的必要条件,s是r的充分条件,q是s的充分条件,那么s、r、p分别是q的什么条件?srpq解由已知r是q的充要条件、p是q的必要条件.s是q的充要条件、7/8/20219特级教师王新敞----源头学子\n二、重难点讲解例3命题p:x=-1或x=2;命题.试判断p是q的什么条件?解:由q中方程解得x=2,x=-1,而x=-1是增根,应舍去,因此q:x=2,所以q的集合B={2},∴p是q的必要不充分条件.由题设P的集合A={-1,2},显然BA,7/8/202110特级教师王新敞----源头学子\n二、重难点讲解若¬q是¬p的充分而非必要条件,求实数m的取值范围.解:由x2-2x+1-m2≤0,得q:1-m≤x≤1+m.所以“¬q”:A={x∈R|x>1+m或x<1-m,m>0}所以“¬p”:B={x∈R|x>10或x<-2}.解得m≥9为所求.另法:¬q是¬p的充分而非必要条件等价于p是q的充分而非必要条件,则[-2,10]就是[1-m,1+m]的真子集.1-m1+m-210由“¬q”是“¬p”的充分而不必要条件知:AB.从而可得7/8/202111特级教师王新敞----源头学子\n二、重难点讲解例5判断:“b2-4ac=0”是“一元二次方程ax2+bx+c=0(a≠0)有两个相等的实根”的什么条件?并证明结论。解:是充要条件.1。充分性:设b2-4ac=0将ax2+bx+c=0(a≠0)配方得:a(x+b/2a)2=(b2-4ac)/4a,(x+b/2a)2=(b2-4ac)/4a2∵b2-4ac=0∴(x+b/2a)2=0∴x1=x2=-b/2a即方程有两个相等的实数根.7/8/202112特级教师王新敞----源头学子\n二、重难点讲解例5判断:“b2-4ac=0”是“方程一元二次方程ax2+bx+c=0(a≠0)有两个相等的实根”的什么条件?并证明结论。解:是充要条件.2。必要性:设方程有两个相等的实数根x1=x2由根与系数的关系有:x1+x2=-b/a;x1x2=c/a∴“b2-4ac=0”是方程ax2+bx+c=0(a≠0)有两个相等实根的充要条件.∵x1=x2,∴2x1=-b/a,x12=c/a可得(-b/2a)2=c/a即b2=4ac,∴b2-4ac=07/8/202113特级教师王新敞----源头学子\n例6求关于x的方程x2+(m-2)x+5-m=0(m∈R)有两个都大于2的实根的充要条件.解:令f(x)=x2+(m-2)x+5-m,则方程x2+(m-2)x+5-m=0的两根都大于2的一个充要条件是抛物线f(x)=x2+(m-2)x+5-m与X轴有两个交点,(特殊情况两个交点重合)并且两个交点在x=2的右侧.此时抛物线满足的充要条件是:解得-5