人教版高中数学课件：分布列 20页

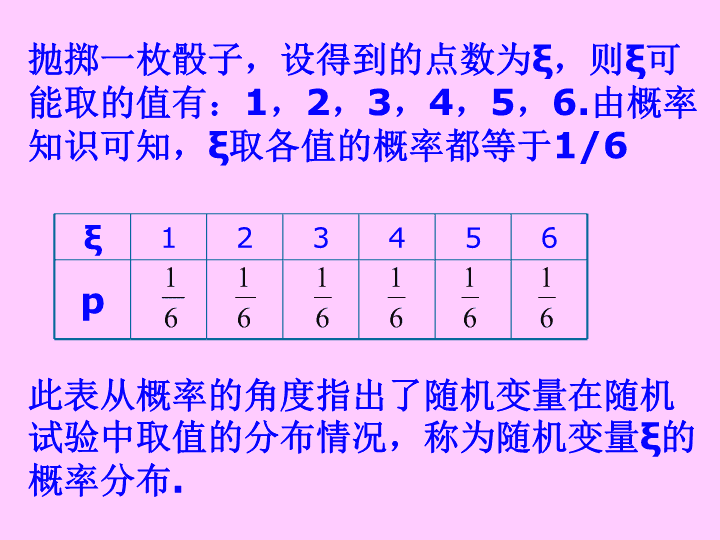
离散型随机变量的分布列\n随机变量：如果随机试验的结果可以用一个变量来表示，那么这样的变量叫做随机变量。离散型随机变量：对于随机变量可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量。连续型随机变量：随机变量可以取某一区间内的一切值，这样的随机变量叫作连续型随机变量。\n抛掷一枚骰子，设得到的点数为ξ，则ξ可能取的值有：1，2，3，4，5，6.由概率知识可知，ξ取各值的概率都等于1/6ξ123456p此表从概率的角度指出了随机变量在随机试验中取值的分布情况，称为随机变量ξ的概率分布.\n例如：抛掷两枚骰子，点数之和为ξ，则ξ可能取的值有：2，3，4，……，12.ξ的概率分布为：ξ23456789101112ｐ\n例1：一盒中放有大小相同的红色、绿色、黄色三种小球，已知红球的个数是绿球个数的两倍，黄球个数是绿球个数的一半，现从该盒中随机取出一球，若取出红球得1分，取出绿球得0分，取出黄球得-1分，试写出从该盒内随机取出一球所得分数ξ的分布列.解：设黄球的个数为ｎ，则绿球的个数为2ｎ，红球的个数为4ｎ，盒中球的个数为7ｎ，所以P（ξ＝1）＝　　＝　　，P（ξ＝0）＝　　＝　　，P（ξ＝-1）＝　　＝　　．所以从该盒中随机取出一球所得分数ξ的分布列为：ξ10-1P\n一般地，设离散型随机变量ξ可能取的值为：ｘ1，ｘ2，……，ｘｉ，……．ξ取每一个ｘｉ（ｉ＝1，2，……）的概率P（ξ＝ｘｉ）＝Ｐｉ，则称表：ξＸ1Ｘ2…Ｘｉ…ＰＰ1Ｐ2…Ｐｉ…为随机变量ξ的概率分布，简称为ξ的分布列.\nξＸ1Ｘ2…Ｘｉ…ＰＰ1Ｐ2…Ｐｉ…离散型随机变量的分布列的两个性质：（1）Ｐｉ≥0，ｉ＝1，2，……；（2）Ｐ1+Ｐ2+……＝1\n例2.一个类似于细胞分裂的物体,一次分裂为二，两次分裂为四，如此进行有限多次，而随机终止，设分裂n次终止的概率是1/2n（n=1，2，3，……）记ξ为原物体在分裂终止后所生成的子块数目,求P（ξ≤10）．解：依题意，原物体在分裂终止后所生成的子块数目ξ的分布列为：……P……16842ξ所以，P（ξ≤10）＝P（ξ＝2）+P（ξ＝4）+P（ξ＝8）＝\n解：根据分布列的性质，针尖想下的概率是（1-p）.于是，随机变量X的分布列是利用分布列和概率的性质，可以计算能由随机变量表示的事件的概率.x01P1-pp2、两点分布列如果随机变量X的分布列为两点分布列，就称X服从两点分布，而称p=P(X=1)为成功概率.例1、在掷一枚图钉的随机实验中，令如果针尖向上的概率为p，试写出随机变量X的分布列.\n例2、在含有5件次品的100件产品中，任取3件，试求：（1）取到的次品数的分布列；（2）至少取到1件次品的概率.3、超几何分布列0123P\n一般地，在含有M件次品的N件产品中，任取n件，其中恰有X件次品数，则事件{X=k}发生的概率为3、超几何分布列称分布列X01…mP…为超几何分布列.如果随机变量X的分布列为超几何分布列，则称随机变量X服从超几何分布.其中m=min{M,n},且nN,MN,n,M,NN*.\n例3、某年级的联欢会上设计了一个摸奖游戏，在一个口袋中有10个红球和20个白球，这些球除颜色外完全相同.一次从中摸出5个球，至少摸到3个红球就中奖.求中奖的概率.中奖的概率为：\n在一次随机试验中，某事件可能发生也可能不发生，在n次独立重复试验中这个事件发生的次数ξ是一个随机变量．如果在一次试验中某事件发生的概率是P，那么在n次独立重复试验中这个事件恰好发生k次的概率是(其中k＝0,1,2,…，n，于是得到随机变量ξ的概率分布如下：ξ01…k…nP……\n由于恰好是二项展开式中的各项的值，所以称这样的随机变量ξ服从二项分布，记作ξ～B(n，p)，其中n，p为参数，并记＝b(k；n，p)．\n例3.（2000年高考题）某厂生产电子元件，其产品的次品率为5%．现从一批产品中任意地连续取出2件，写出其中次品数ξ的概率分布．解：依题意，随机变量ξ～B(2，5%)．所以，因此，次品数ξ的概率分布是ξ012P0.90250.0950.0025\n例4.重复抛掷一枚筛子5次得到点数为6的次数记为ξ，求P(ξ>3)．解：依题意，随机变量ξ～B．\n1.一个袋中有6个同样大小的小球，编号为1，2，3，4，5，6，现从中随机取出3个球，以ξ表示取出的最大号码，求ξ的分布列.练习：\n2.设随机变量ξ的分布（1）求常数的值；（2）求（3）求.练习：\n3.袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为1/7，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取……，取后不放回，直到两人中有一人取到白球时既终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数。（1）求袋中原有白球的个数；（2）求随机变量的概率分布；（3）求甲取到白球的概率.练习：\n4.袋A和B中装有白球和黑球若干，从A中任取1个球白球的概率都是为1/3，从A中任取1个球白球的概率都是为P,甲先取，乙后取，然后甲再取……，取后不放回，直到两人中有一人取到白球时既终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数。（1）求袋中原有白球的个数；（2）求随机变量的概率分布；AAABBBBB（3）求甲取到白球的概率.练习：