- 1.21 MB
- 2022-08-05 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
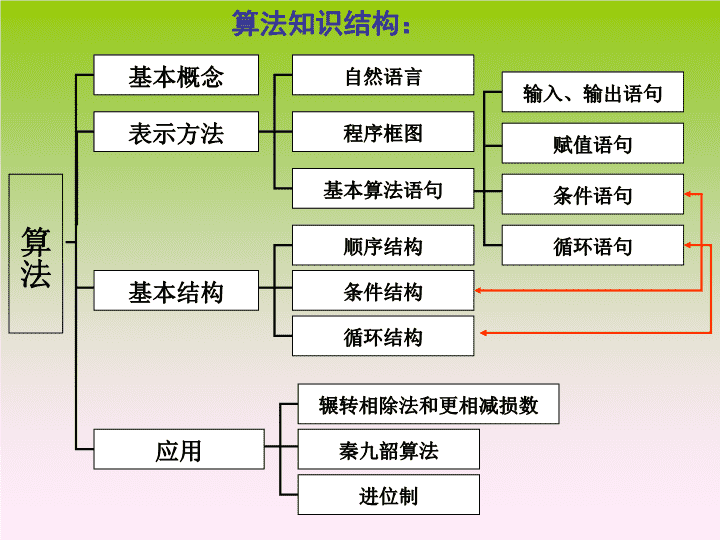
第一章算法\n算法知识结构:基本概念算法基本结构表示方法应用自然语言程序框图基本算法语句顺序结构条件结构循环结构辗转相除法和更相减损数秦九韶算法进位制赋值语句条件语句循环语句输入、输出语句\n一、考查程序框图、语句的功能例1、如图给出了一个算法流程图,该算法流程图的功能是()A.求a,b,c三数的最大数B.求a,b,c三数的最小数C.将a,b,c按从小到大排序D.将a,b,c按从大到小排序\n例2、如图是一个算法的程序框图,当输入的值x为5时,则其输出的结果是。\n例3、根据框图,回答下列问题:(1)若输入的x值为5,则输出的结果是:;(2)要输出的值为8,则输入的x是;(3)要使输出的值最小,输入的x的范围是。\n二、完善程序框图中的条件或内容例4、如图,若框图所给的程序运行结果为s=132,那么判断框中应填入的关于k的判断条件是。\n例5、上图是的程序框图,判断框应填入的内容是,处理框应填入的内容是。\n三、算法与其他知识的综合例6、如图是某县参加2007年高考的学生身高条形统计图,从左到右的各条形图表示学生人数依次记为A1、A2、…A10(如A2表示身高(单位:cm)在[150,155内的人数。图2是统计图1中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是(A)i<6(B)i<7(C)i<8(D)i<9\n\n例7、阅读程序框图,若输入的是100,则输出的变量和的值依次是()A.2500,2500B.2550,2550C.2500,2550D.2550,2500\n例8、甲、乙两人玩游戏,规则如流程图所示,则甲胜的概率是。\n例9、义乌市居民用水原价为2.25元/立方米,从2008年1月1日起实行阶梯记价:其中p是用水总量的一次函数,已知用水总量40时p=3.0元/立方米,用水总量50是p=3.5元/立方米1.写出水价调整后居民每月水费总额与用水量的函数关系式;2.用流程图描述水价调整后计算水费的过程。级数每月计算水费的用水量价格元/立方米1不超过20立方米的1.82超过20立方米至30立方米的2.43超过30立方米的p\n例10、阅读图中的流程图,回答下面问题:1.若a<b<c,则输出的数是;2.若,则输出的数是。\n例11、为确保信息安全,信息需要加密传输,发送方由明文密文(加密),接受方有密文明文(解密),已知加密规则如图所示,例如,输入明文1,2,3,4则对应加密文5,7,18,16。若接受方收到密文14,9,23,28时,则解密得到的明文为:()A.4,6,1,7B.7,6,1,4C.6,4,1,7D.1,6,4,7\n第二章统计\n统计用样本估计总体随机抽样简单随机抽样系统抽样分层抽样变量间的相关关系用样本的频率布估计总体分布用样本的数字特征估计总体数字特征线性回归分析知识结构\n知识梳理1.简单随机抽样(1)思想:设一个总体有N个个体,从中逐个不放回地抽取n个个体作为样本,如果每次抽取时总体内的各个个体被抽到的机会都相等,则这种抽样方法叫做简单随机抽样.\n抽签法:第一步,将总体中的所有个体编号,并把号码写在形状、大小相同的号签上.第二步,将号签放在一个容器中,并搅拌均匀.第三步,每次从中抽取一个号签,连续抽取n次,就得到一个容量为n的样本.(2)步骤:\n随机数表法:第一步,将总体中的所有个体编号.第二步,在随机数表中任选一个数作为起始数.第三步,从选定的数开始依次向右(向左、向上、向下)读,将编号范围内的数取出,编号范围外的数去掉,直到取满n个号码为止,就得到一个容量为n的样本.\n2.系统抽样(1)思想:将总体分成均衡的n个部分,再按照预先定出的规则,从每一部分中抽取1个个体,即得到容量为n的样本.(2)步骤:第一步,将总体的N个个体编号.第二步,确定分段间隔k,对编号进行分段.第三步,在第1段用简单随机抽样确定起始个体编号.第四步,按照一定的规则抽取样本.\n3.分层抽样(1)思想:若总体由差异明显的几部分组成,抽样时,先将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,再将各层取出的个体合在一起作为样本.(2)步骤:第一步,计算样本容量与总体的个体数之比.第二步,将总体分成互不交叉的层,按比例确定各层要抽取的个体数.第三步,用简单随机抽样或系统抽样在各层中抽取相应数量的个体.第四步,将各层抽取的个体合在一起,就得到所取样本.\n总结:不管哪种抽样,在每一次抽取时每个个体被抽到概率都是大N分之一,在整个过程中每个个体被抽取的概率都是大N分之小n\n4.频率分布表(1)含义:表示样本数据分布规律的表格.(2)作法:第一步,求极差.第二步,决定组距与组数.第三步,确定分点,将数据分组.第四步,统计频数,计算频率,制成表格.\n5.频率分布直方图(1)含义:表示样本数据分布规律的图形.(2)作法:第一步,画平面直角坐标系.第二步,在横轴上均匀标出各组分点,在纵轴上标出单位长度.第三步,以组距为宽,各组的频率与组距的商为高,分别画出各组对应的小长方形.每个小距形的面积等于频率,频数之比等于频率之比等于面积之比等于距形的高之比\n6.频率分布折线图在频率分布直方图中,依次连接各小长方形上端中点得到的一条折线,称为频率分布折线图.7.总体密度曲线当总体中的个体数很多时,随着样本容量的增加,所分的组数增多,组距减少,相应的频率分布折线图越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.\n8.茎叶图作法:第一步,将每个数据分为“茎”(高位)和“叶”(低位)两部分;第二步,将最小的茎和最大的茎之间的数按大小次序排成一列,写在左(右)侧;第三步,将各个数据的叶按大小次序写在茎右(左)侧.\n9.众数、中位数和平均数众数:频率分布直方图最高矩形下端中点的横坐标.中位数:频率分布直方图面积平分线的横坐标.(中位数两边面积相等且等于0.5)平均数:频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积的总和.\n10.标准差11.相关关系自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系,叫做相关关系.12.散点图在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.\n如果散点图中的点的分布,从整体上看大致在一条直线附近,则称这两个变量之间具有线性相关关系,这条直线叫做回归直线.13.回归直线14.回归方程\n例1.某工厂人员及周工资构成如下:人员经理管理人员高级技工工人学徒合计周工资2200250220200100人数16510123合计22001500110020001006900(1)指出这个问题中周工资的众数、中位数、平均数.(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么?200,220,300.\n(2)因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平.\n例2.以往招生统计显示,某所大学录取的新生高考总分的中位数基本稳定在550分,若某同学今年高考得了520分,他想报考这所大学还需收集哪些信息?解析:(1)查往年录取的新生的平均分数.若平均数小于中位数很多,说明最低录取线较低,可以报考.(2)查往年录取的新生高考总分的标准差.若标准差较大,说明新生的录取分数较分散,最低录取线可能较低,可以考虑报考.\n例3.为了了解某城市中学生的身体发育情况,对某中学的50名男生抽样测量,其身高记录如下(单位:cm):176,175,168,170,167,181,162,173,171,177,157,179,172,165,172,173,166,177,169,181,177,160,163,166,175,174,173,174,171,171,175,158,170,165,165,174,169,163,166,166,172,174,172,166,167,172,175,161,173,167.(1)列出频率分布表;(2)作出频率分布直方图和累积频率分布图;(3)估计身高在168.5~176.5内的概率;(4)估计身高超过178.5的概率.\n解:(1)频率分布表如下:分组频数频率累积频率156.5~160.530.060.06160.5~164.540.080.14164.5~168.5120.240.38168.5~172.5120.240.62172.5~176.5130.260.88176.5~180.540.080.96180.5~184.520.041.00合计501.00\n(2):频率分布直方图:156.5160.5164.5168.5172.5176.5180.5184.5身高频率组距\n(3)身高在168.5~176.5以内的概率为0.88-0.38=0.50.(4)在累积频率分布图中,横坐标为178.5落在区间[176.5,180.5)内,在这段区间上的折线段的两端点分别是(176.5,0.88),(180.5,0.96),所在的直线方程为y=0.02x-2.65,令x=178.5,代入求得y=0.92,即身高不超过178.5的概率为92%.于是身高超过178.5的概率为8%.\n【1】对具有线性相关关系的变量x和y,测得一组数据如下表:x24568y3040605070若已求得它们的回归直线方程的斜率为6.5,则这条回归直线的方程是().变量间的相关关系A\n【2】已知回归直线斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为().C\n【3】(济宁一模理)某考察团对全国10个城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查,y与x具有相关关系,回归方程y=0.66x+1.562,若某城市居民人均消费水平为7.675(千元),估计该城市人均消费额占人均工资收入的百分比约为()A.83%B.72%C.67%D.66%A\n【4】下列有关线性回归的说法不正确的是().A.变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系B.在平面直角坐标系中用描点的方法得到具有相关关系的两个变量的一组数据的图形叫做散点图C.线性回归直线得到具有代表意义的回归直线方程D.任何一组观测值都能得到具有代表意义的回归直线方程练一练D\n第三章概率\n概率知识点:1、频率与概率的意义3、古典概型4、几何概型2、事件的关系和运算\n1、频率本身是随机的,在试验前不能确定。做同样次数的重复试验得到事件的频率会不同。2、概率是一个确定的数,与每次试验无关。是用来度量事件发生可能性大小的量。3、频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率。频率与概率的意义:\n事件的关系和运算:(2)相等关系:(3)并事件(和事件):(4)交事件(积事件):(5)互斥事件:(6)互为对立事件:(1)包含关系:且是必然事件A=B\n互斥事件与对立事件的联系与区别:1、两事件对立,必定互斥,但互斥未必对立2、互斥的概念适用于多个事件,但对立概念只适用于两个事件3、两个事件互斥只表明这两个事件不能同时发生,即至多只能发生一个,但可以都不发生;而两事件对立则表明它们有且只有一个发生\n概率的基本性质(1)0≤P(A)≤1(2)当事件A、B互斥时,(3)当事件A、B对立时,\n(1)试验中所有可能出现的基本事件只有有限个;(有限性)(2)每个基本事件出现的可能性相等。(等可能性)古典概型1)两个特征:2)古典概型计算任何事件的概率计算公式为:\n(1)试验中所有可能出现的结果(基本事件)有无限多个.(2)每个基本事件出现的可能性相等.几何概型1)几何概型的特点:2)在几何概型中,事件A的概率的计算公式如下:\n1.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是()B.C.D.A.\n2、某种彩票中奖几率为0.1%,某人连续买1000张彩票,下列说法正确的是:()A、此人一定会中奖B、此人一定不会中奖C、每张彩票中奖的可能性都相等D、最后买的几张彩票中奖的可能性大些\n3.一批产品中,有10件正品和5件次品,对产品逐个进行检测,如果已检测到前3次均为正品,则第4次检测的产品仍为正品的概率是()A.7/12B.4/15C.6/11D.1/34、在去掉大小王的52张扑克中,随机抽取一张牌,这张牌是J或Q的概率为_________\n5.有一人在打靶中,连续射击2次,事件“至少有1次中靶”的对立事件是()A.至多有1次中靶B.2次都中靶C.2次都不中靶D.只有1次中靶6、甲、乙两人下棋,两人下和棋的概率为,乙获胜的概率为,则甲获胜的概率为_______________7、在相距5米的两根木杆上系一条绳子,并在绳子上挂一盏灯,则灯与两端距离都大于2米的概率为______________\n8、将甲、乙两颗骰子先后各抛一次,a,b分别表示抛掷甲、乙两颗骰子所得的点数,若把点数P(a,b)落在不等式组所表示的区域的事件记为A,求P(A)\n9、袋中有红、白色球各一个,每次任意取一个,有放回地抽三次,(1)三次颜色中恰有两次同色的概率?(2)三次颜色全相同的概率?(3)抽取的红球多于白球的概率?\n10、从1,2,3,4,5五个数字中任意取2个出来组成一个没有重复数字的两位数,求(1)这个两位数是奇数的概率。(2)这个两位数大于30的概率。(3)求十位和个位上数字之和大于4两位数的概率。\n11、有一个半径为4的圆,现将一枚直径为2的硬币投向其中,(硬币完全落在圆外的不计),则硬币完全落在圆内的概率?思考:半径为4的圆改为:边长为4的正方形?\nAO如图:OA=2,OB=5,在线段OB上任意取一点P,试求:B(1)三角形AOP为钝角三角形的概率(2)三角形AOP为锐角三角形的概率12、\n13、甲乙两辆货车都要停靠同一个站台卸货,他们可能在一昼夜的任一时刻到达,甲乙两辆货车卸货的时间分别是6小时与4小时。求有一辆货车停靠站台时不需等待的概率。\n14、鞋柜有3双不同的鞋,随机取出2只,试求下列事件的概率:(1)取出的鞋不成对;(2)取出的鞋都是左脚的;(3)取出的鞋都是同一只脚的;(4)取出的鞋一只是左脚的,一只是右脚的,但它们不成对。