【高中数学课件】立体几何习题课ppt课件 11页

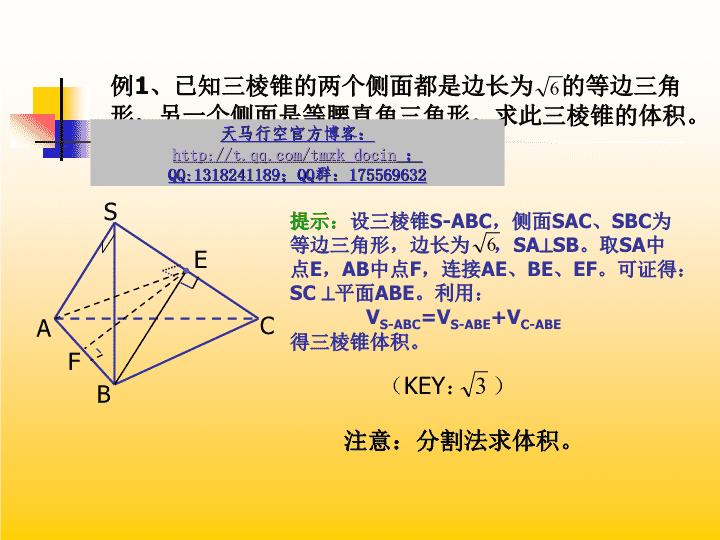
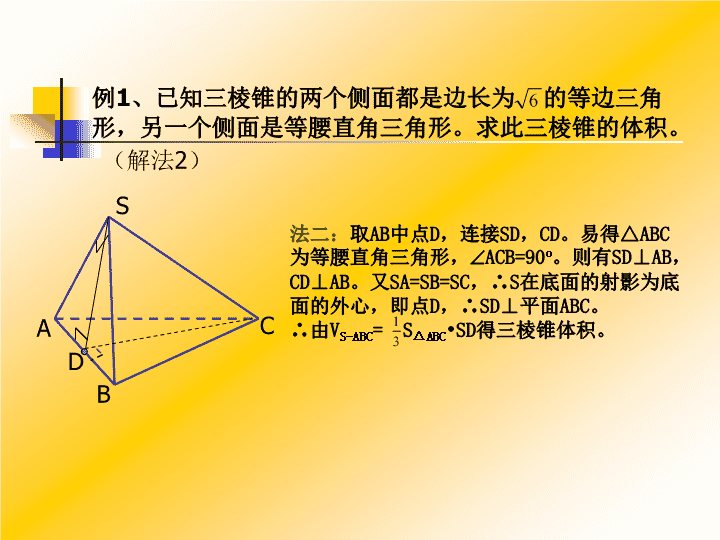
立体几何习题课\n例1、已知三棱锥的两个侧面都是边长为的等边三角形，另一个侧面是等腰直角三角形。求此三棱锥的体积。ABCSEF提示：设三棱锥S-ABC，侧面SAC、SBC为等边三角形，边长为，SASB。取SA中点E，AB中点F，连接AE、BE、EF。可证得：SC平面ABE。利用：VS-ABC=VS-ABE+VC-ABE得三棱锥体积。注意：分割法求体积。（KEY：）\nABCSD例1、已知三棱锥的两个侧面都是边长为的等边三角形，另一个侧面是等腰直角三角形。求此三棱锥的体积。法二：取AB中点D，连接SD，CD。易得△ABC为等腰直角三角形，ACB=90o。则有SD⊥AB，CD⊥AB。又SA=SB=SC，∴S在底面的射影为底面的外心，即点D，∴SD⊥平面ABC。∴由VS-ABC=S△ABC•SD得三棱锥体积。（解法2）\n例2、在棱长为a的正方体ABCD-A1B1C1D1中，求D1到截面C1BD的距离。ABCDA1B1C1D1提示：利用=求解。注意：等体积法求点面距离。KEY：\n例3、在各棱长均为1的正三棱柱ABC-A1B1C1中，（1）BC1与侧面ABB1A1所成的角为__________；（2）如果M为CC1的中点，则截面AB1M与底面所成的角的大小为__________。ABCA1B1C1DB1ABCA1C1MN注：（1）中利用面面垂直的性质找线面成角。（2）中射影面积公式的应用：S△AB1M•cosα=S△ABC.45o\n例4、三棱锥V-ABC中，VA底面ABC，ABC=90o，VA=a，VB=b，AC=c（cb），M是VC中点。（1）求证：V，A，B，C四点在以M为球心的球面上；（2）求VC与AB所成的角的大小。AVBCMEFG\n例5、已知三棱锥P-ABC，PA=BC=5，PB=AC=，PC=AB=，求三棱锥的体积。提示：分别以三组对棱作为一长方体的相对面的对角线，将原三棱锥补成一个长方体，如图，则VP-ABC=V长方体-4V。设长方体长宽高分别为a、b、c，则有：所以三棱锥P-ABC的体积为20（立方单位）。PABCPABCP`A`B`C`\n例6、三棱锥P-ABC中，AP=AC，PB=2，将此棱锥沿三条侧棱剪开，其展开图是一个直角梯形P1P2P3A。（1）求证：侧棱PB⊥AC；（2）求侧面PAC与底面ABC所成的角的余弦值。ABCPDBP1P2P3ADCEӨ22mmmnn（甲）（乙）\nBP1P2P3ADCE22mmmnnABCPDӨ解:(1)（略）(2)甲图中，作PD⊥AC于D，连接BD，可得PDB即为面PAC与面ABC所成二面角的平面角。乙图中，作AE⊥CP3于E点，则AE=P1P2=4。∵PA=AC，即P3A=AC，∴E为CP3的中点。设AP1=AC=AP3=m，CE=EP3=n，由CP2=CP3得：m-n=2nm=3n……①又在△ACP3中有：AE•CP3=AC•DP3……②，而AE=4……③，由①②③得：DP3=8/3，即PD=8/3。∴甲图Rt△BPD里，BD=10/3，∴cosPDB=4/5,为所求。（甲）（乙）2\n如图，有一轴截面为正三角形的圆锥形容器，内部盛水高度为h，放入一个小球后，水面恰好与球相切，求球的半径。R2RhV1V2V2=V1+V球课本P81第8题\n小结：1、分割法求体积；2、利用射影面积法求二面角；3、补形法求体积；4、几何体展开问题。