高中数学立体几何常考证明题汇总-高中课件精选 9页

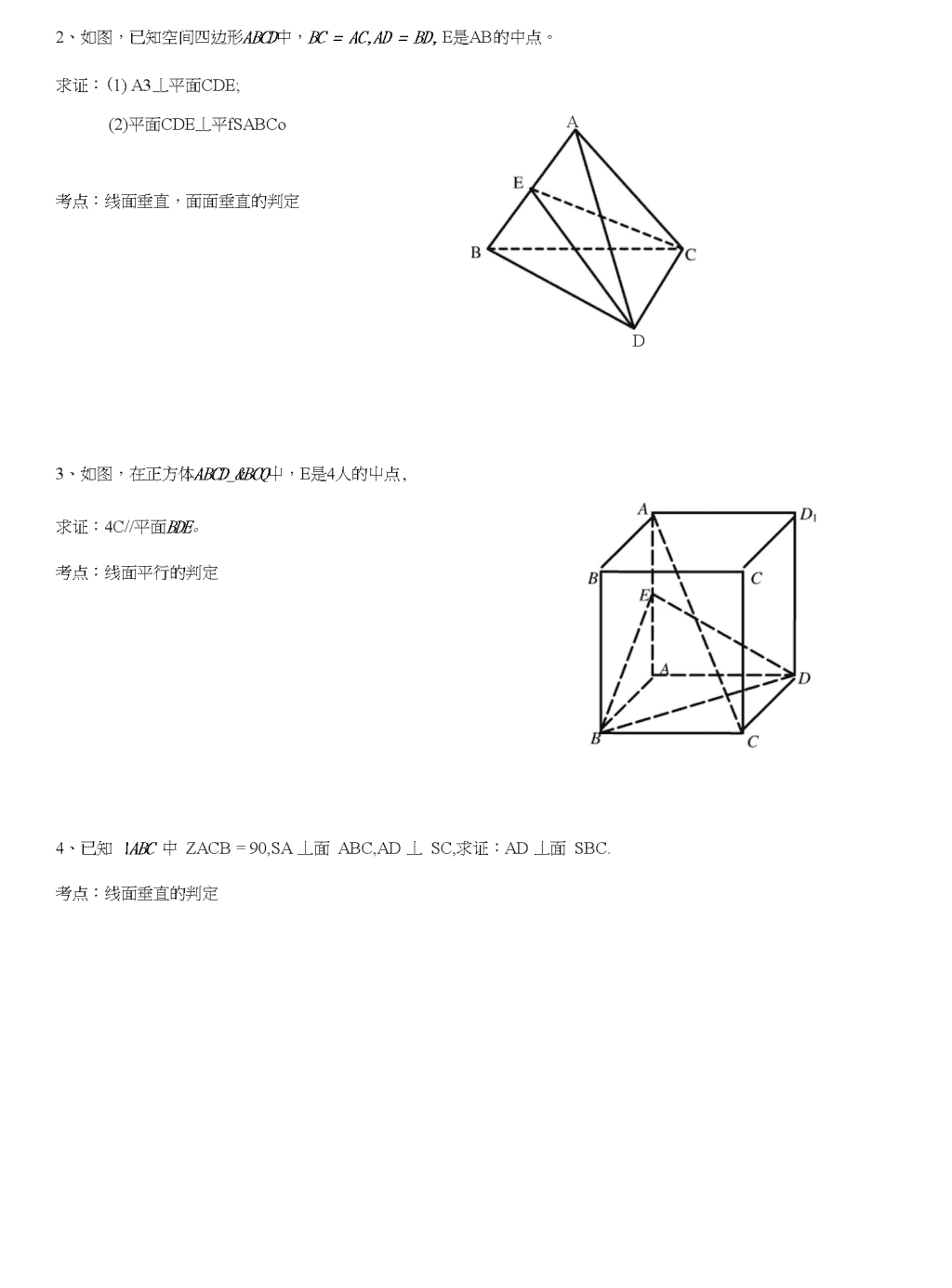
立体几何选择题：一、三视图考点透视：①能想象空间几何体的三视图，并判断（选择题）.②通过三视图计算空间几何体的体积或表面积.③解答题中也可能以三视图为载体考查证明题和计算题.1.一空间几何体的三视图如图2所示，该几何体的体积为12龙+座，3则正视图屮x的值为（）A.5B.4C.3D.22•在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为程D）AQ□\[hAAABCD3.如图4,已知一个锥体的正视图（也称主视图），左视图（也称侧视图）和俯视图均为直角三角形，且面积分别为3,4,6,则该锥体的体积是.w㈢牛4.某四棱锥的三视图如图1一1所示，该四棱锥的表而积是（B）A.32B.16+16^2C.48D.16+32迈二、直观图掌握直观图的斜二测画法：①平行于两坐标轴的平行关系保持不变；②平行于y轴的长度为原来的一半，x轴不变；③新坐标轴夹角为45°或135°o1、利用斜二侧画法画水平放置的平面图形的直观图，得到下列结论，其中正确的是（）A.正三角形的直观图仍然是正三角形.B.平行四边形的直观图一定是平行四边形.C.正方形的直观图是正方形.D.圆的直观图是圆2、如图，梯形AMD、是一平面图形理磁的直观图（斜二测），若A\D\〃Uy\,AR//GR,〃/=2,G〃=3,仙D.l(h/2=1,则梯形/册的面积是（）A.10B.5C.5^/2三、表面积和体积不要求记忆，但要会使用公式。审题时分清“表面积”和“侧面积”。（1）圆柱、锥.台的侧面积，球的表面积公式。（2）柱.锥.台体，球体的体积公式。（3）正方体的内切球和外接球：内切球半径？外接球直径?（4）扇形的面积公式s=-lr=丄a厂$弧长公式/=0厂22\n1、一个直角三角形的两条直角边分别是3和4,以它的斜边为轴旋转所得的旋转体的表面积为()A.84—7T5C.36龙D.24龙2、若圆锥的高是底面半径和母线的等比屮项，则称此圆锥为“黄金圆锥”。C知某黄金圆锥的侧面积为小贝9这个圆锥的高为13、将圆心角为120P,面积为3龙的扇形，作为圆锥的侧面，则圆锥的表面积为4、若一个球的体积是4屁，则它的表面积为•四.线.面的位置1、下列四个命题中假命题的个数是()A①两条直线都和同一个平面平行，则这两条直线平行。②两条直线没有公共点，则这两条直线平行。③两条直线都和第三条直线垂直，则这两条直线平行。④all卩、ciuoc、bu卩nallb。A.4B.3C.2D.12、阅读以下命题：①如果是两条直线，且allb,那么a平行于经过b的所有平面.②如果直线d和平面&满足alia,那么。与a内的任意直线平行.③如果直线a,b和平面a满足alla.bHa,那么allb.④如果直线a,方和平面a满足allb.alla.ba,那么bIIa.⑤如果平面a丄平面y，平面0丄平面Y，aCl0=/,那么/丄平面Y.请将所有正确命题的编号写在横线上•3＞设％〃是两条不同的直线，是两个不同的平面，下列命题正确的是()(A)若m丄n,m丄a.nll/?,则a丨丨0B)若mlla,nl丨卩、a丨10,则加//n(C)若力丄a.n!I/3,a11p,则加丄(D)若mHn.mlla,nil[3,则a//0立体几何常考证明题:1、已知四边形ABCD是空间四边形，E,F,G,H分别是边AB.BC.CD.DA的屮点(1)求证：EFGII是平行四边形(2)若BD=2^3,AC二2,EG=2。求异面直线AC、BD所成的角和EG、BD所成的角。C\n2、如图，已知空间四边形ABCD中，BC=AC,AD=BD,E是AB的中点。求证：(1)A3丄平面CDE;(2)平面CDE丄平fSABCo考点：线面垂直，面面垂直的判定AD3、如图，在正方体ABCD_&BCQ屮，E是4人的屮点,求证：4C//平面BDE。考点：线面平行的判定4、已知\ABC中ZACB=90,SA丄面ABC,AD丄SC,求证：AD丄面SBC.考点：线面垂直的判定\nB5、已知正方体ABCD-A&CP，0是底ABCD对角线的交点.\n求证：（1）CQ〃面；（2）AC丄面ABQ・考点：线面平行的判定（利用平行四边形），线面垂直的判定6、正方体ABCD-A'B'C'D'中，求证：（1）AC丄平面B‘DDB；⑵BD丄平面ACB'考点：线面垂直的判定7、正方体ABCD—AXBXCXD｛中.（1）求证：平面A/D〃平面（2）若E、F分别是必1，CC|的屮点，求证：平面EB\D\〃平面FBD.考点：线面平行的判定（利用平行四边形）8＞如图P是AABC所在平面外一点，PA=PB,CB丄平面PAB,M.是PC的中点，N是AB±的点,AN=3NBAP（1）求证：MN丄AB；（2）当ZAPB=90,AB=2BC=4.时，求MN的长。/\考点：三垂线定理M力\\n平面BDG.考点：线面平行的判定(利用三角形中位线)10、如图，在正方体ABCD-A^C.D,中，E是人£的中点.(1)求证：4C7/平面BDE；(2)求证：平面A.AC丄平面BDE.考点：线面平行的判定(利用三角形中位线)，面面垂直的判定11、如图，在四棱锥P-ABCD中，底面ABCD是ZD4B=60°且边长为d的菱形，侧面PAD是等边三角形,且平而PAD垂直于底面ABCD.(1)若G为AD的中点，求证：BG丄平面PAD；P(2)求证：AD丄PB；\n(3)求二面角A-BC-P的大小.考点：线面垂直的判定，构造直角三角形，面面垂直的性质定理，二面角的求法(定义法)14、如图1，在正方体ABCD—ABd中，M为CC；的中点，AC交BD于点、0,求证：4,0丄平面MBD.考点：线面垂直的判定，运用勾股定理寻求线线垂直(设棱长为a)1.证明：在AABD中，•:E、H分别是AB,AD的中点EHIIBD,EH=’BD2同理，FG//BD,FG」BD:.EHIIFG,EH=FG:.四边形EFGH是平行四边形。2⑵90°30°2•证明：(1)BC=ACAE=BE^CELAB同理,AD=BDAE=BEnDE丄AB又•/CEcDE=E:.AB丄平面CDE(2)由(1)有AB丄平iffiCDE\n3.证明：连接AC交3D于。，连接E0,・・・E为44的中点，。为AC的中点・・・E0为三角形A.AC的中位线AEOHA.C又E0在平面BDE内，4C在平面BDE外・・・AC//平血BDE。4.证明：JZACB=90°・•・BC丄AC又SA丄面ABC..SA丄BC・•・BC丄面SAC・•・BC丄AD又SC丄AD,SCcBC=C/.AD丄而SBC5.证明：(1)连结4G，设连结aq・・・ABCD-A^C^是正方体・•.4ACC,是平行四边形:,A\C\//AC且AG=AC又q,0分别是AC，AC的中点，・・・O|C|〃A0且O}C}=AO•••AOCQ是平行四边形.・.CQ〃Aq,Aqu面售Q,eg面ABQi・・・CQ〃面ABQ(2)eq丄面:.eq丄耳i又・・・AG丄BQ.・.B\D\丄面AG即AC丄B\D\同理可证AC丄A。，又DbnAf),=D}/.AjC丄面ABlDi6.无答案7.证明：⑴由B\B//DD\,得四边形BBQiD是平行四边形,・・・B\D\//BD,又BDu平面B\D\C,BiDjU平面B]D】C,・・・BD〃平面BQ|C.同理4|D〃平面B\D\C.ffljAlDQBD=Df・••平而A/D〃平BXCD.(2)由BD//B\D\,得BD〃平面EB\D、・取BB]屮点G,:.AE〃B\G.从而得5E〃AG,同理GF〃AD.・・・AG〃DF.・・・5E〃£>F.・・・DF〃平面EBQi.・••平面EBQi〃平面FBD.\n3.证明：(1)取P4的中点Q,连结MQ,NQ,•:M是戶〃的中点，AMQ//BC,・・・C3丄平面PAB,.・.MQ丄平面PAB:.QN是MN在平面内的射影，取A〃的中点D,连结PD,*.*M®PD丄4B,又働,・・・BN=ND:.QN//PD,:.QN丄A3,由三垂线定理得MN丄43(2)•:ZAPB=90,PA=PB,：・PD=LaB=2,：・QN=\,VMQ丄平面PAB,：.MQ丄NQ,且MQ=-BC=1,:.MN=414.证明：・・•£、F分别是AB.AD的中点，:.EF〃BD又EF