高中数学 复习课件 新人教A必修1 39页

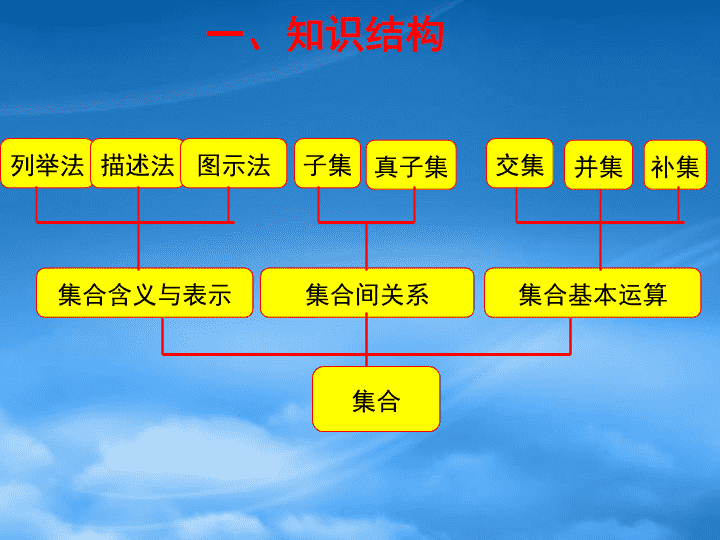
必修1复习\n集合集合含义与表示集合间关系集合基本运算列举法描述法图示法子集真子集补集并集交集一、知识结构\n{}211-，，=M2.已知集合集合则M∩N是()AB{1}C{1，2}　DΦ{}，，MxxyyNÎ==2练习1.集合A={1,0,x},且x2∈A,则x＝_____3.满足{1,2}A{1,2,3,4}的集合A的个数有个-1B4变式：变式：设集合,则满足的集合B的个数是___4\n4.集合S，M，N，P如图所示，则图中阴影部分所表示的集合是()(A)M∩(N∪P)(B)M∩CS(N∩P)(C)M∪CS(N∩P)(D)M∩CS(N∪P)D\n作业讲评(-∞,-1]或12.其中,如果，求实数a的取值范围\n设全集为R，集合，（1）求：A∪B，CR(A∩B)；（2）若集合,满足，求实数a的取值范围.{x|x≥-1};{x|x≥3或x<2};{a|a>-4}\n7.设,且，求实数的a取值范围.\n知识结构概念三要素图象性质指数函数应用大小比较方程解的个数不等式的解实际应用对数函数函数\n函数的概念BCx1x2x3x4x5y1y2y3y4y5y6A函数的三要素：定义域，值域，对应法则A.B是两个非空的集合,如果按照某种对应法则f，对于集合A中的每一个元素x，在集合B中都有唯一的元素y和它对应，这样的对应叫做从A到B的一个函数.\n函数定义域奇偶性图象值域单调性指数函数对数函数函数的复习主要抓住两条主线1、函数的概念及其有关性质.2、几种初等函数的具体性质.幂函数\n例:已知集合A=(a,b,c},B={-1,0,1},映射f:A→B满足f(a)+f(b)=f(c),求这样的映射共有多少个?f(a)=-1,f(b)=1,f(c)=0;f(a)=1,f(b)=-1,f(c)=0;f(a)=f(b)=f(c)=0;f(a)=-1,f(b)=0,f(c)=-1;f(a)=0,f(b)=-1,f(c)=-1;f(a)=1,f(b)=0,f(c)=1;f(a)=0,f(b)=1,f(c)=1.\n指数函数1、定义域.2、值域3、单调性4、图象a>10100,则幂函数过点(0,0)、(1,1),在(0,+∞)上为增函数;\n函数的定义域：使函数有意义的x的取值范围.求定义域的主要依据1、分式的分母不为零.2、偶次方根的被开方数不小于零.3、零次幂的底数不为零.4、对数函数的真数大于零.5、指、对数函数的底数大于零且不为1.6、实际问题中函数的定义域\n2.1.求函数的定义域.\n求函数的解析式：1,已知求f(x).2,已知f(x)是一次函数，且f[f(x)]=4x+3求f(x).3，已知求f(x).\n求值域的一些方法：1、图像法，2、配方法，3、逆求法，4、分离常数法，5、换元法，6单调性法.a)b)c)d)\n函数的单调性：如果对于属于这个区间的任意两个自变量的值x1,x2,当x1f(x2),那么就说f(x)在这个区间上是减函数.\n单调性的应用（局部特征）当x1f(x2)函数f(x)在区间D上是减函数题型1：由（1）（2）推出（3）⑴⑵⑶题型2：由（2）（3）推出（1）题型3：由（1）（3）推出（2）应用：单调性的证明应用：求自变量的取值范围应用：可得因变量的大小\n变式1、函数在[5，20]上为单调函数，求实数的取值范围.例题1、函数,当时是增函数，当时是减函数，则的值为_________.变式2、函数，在上为单调增函数，求实数的取值范围.25k≤40或k≥160a≥-1\n变式:已知是定义在上的奇函数，函数在上单调递增，满足，数的取值范围是______(0,1)\n一、函数的奇偶性定义前提条件：定义域关于原点对称.1、奇函数f(-x)=-f(x)或f(-x)+f(x)=02、偶函数f(-x)=f(x)或f(-x)-f(x)=0二、奇函数、偶函数的图象特点1、奇函数的图象关于原点成中心对称图形.2、偶函数的图象关于y轴成轴对称图形.\n若函数　　　　　　　为奇函数，求a.\n奇偶性的应用例题　、已知函数且，则变式1、已知函数都为上奇函数且，则\n2.已知函数f(x)是定义为（0，+）上的增函数，且满足f(xy)=f(x)+f(y),(x,yR+),f(2)=1求：1）f(1)值；2)满足f(x)+f(x-3)<2的x的取值范围\n1．下列图形中，可以作为y是x的一个函数的图象是ABCDxyxylg2,lg2==xyOxyOxyOxOy\n2.点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是()lxyooPAoPBoPCoPDC\n3.设计四个杯子的形状,使得在向杯中匀速注水时,杯中水面的高度h随时间t变化的图象分别与下列图象相符合.tho图(1)\ntho图(2)tho图(3)\ntho图(4)\n4.如图(1)是某条公共汽车线路收支差额y与乘客量x的图象.(1)说明图(1)上点A，点B以及射线AB上的点的实际意义；　　　　　　　　(2)由于目前本线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图(2),(3)所示,说明这两种建议是什么?tho图(1)AB-11.5tho图(2)AB-11.5tho图(3)AB-11.5\n例作函数的图象.yxo1yxo1\n练习：如何由的图象作出的图象.\n1.已知奇函数是定义在上的减函数，且不等式　　　　　　　　　的解集为　，求函数的最大值．函数综合应用\n2.如图,将一块半径为1的半圆形钢板,切割成等腰梯形ABCD,其下底边AB是圆O的直径,上底边CD的端点在圆周上,设梯形的一条腰长为x,周长为f(x),求函数f(x)的值域.BACDE\n\n函数综合应用解析\n