2014高中数学平面向量课件精品 66页

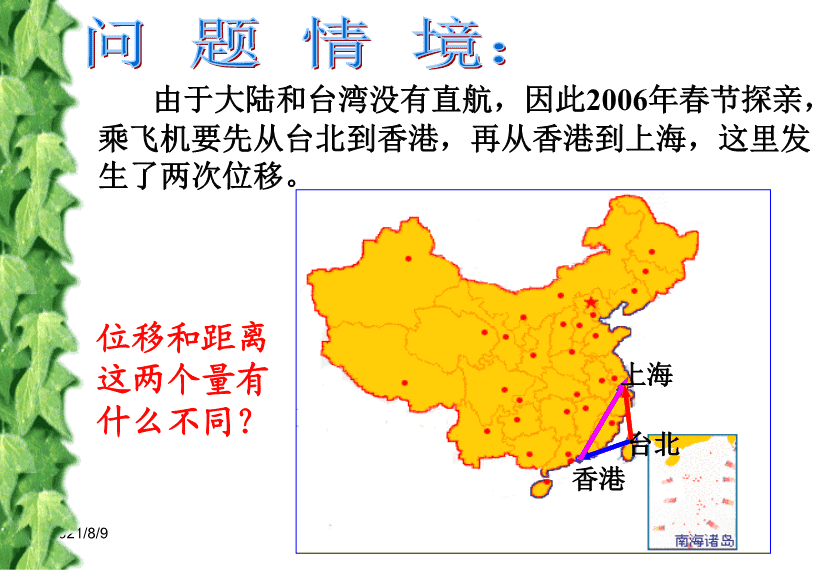
2021/8/9Welcome\n2021/8/9请问：金钱豹能追上小狗吗？为什么？问题情境：金钱豹以5m/s的速度追赶一只以2m/s逃跑的小狗……\n2021/8/9由于大陆和台湾没有直航，因此2006年春节探亲，乘飞机要先从台北到香港，再从香港到上海，这里发生了两次位移。台北香港上海问题情境：位移和距离这两个量有什么不同？\n2021/8/9F=20NV=20km/h（2）（3）都是有大小和方向的量m=20kg(1)(2)(3)观察下述三个量有什么区别？合作探究：\n2021/8/9向量的概念及表示资中县第一中学高一数学组*\n2021/8/9二、向量的表示方法AＢ②也可以表示：abcd….a一、向量的定义既有大小又有方向的量向量的模大小记为┃a┃①几何表示——向量常用有向线段表示：有向线段的长度表示向量的大小，箭头所指的方向表示向量的方向。以A为起点、B为终点的向量记为：ＡＢ。大小记着：│AB│向量的长度\n2021/8/9我们现在研究的向量，与起点无关，用有向线段表示向量时，起点可以取任意位置。所以数学中的向量也叫自由向量如图：他们都表示同一个向量。不是，温度只有大小，没有方向。不是，方向不同1、温度有零上和零下之分，温度是向量吗？为什么？2、向量AB和BA同一个向量吗？为什么？aa说明1：小试牛刀\n2021/8/9有向线段与向量的区别：有向线段：有固定起点、大小、方向向量：可选任意点作为向量的起点、有大小、有方向。ABCDABCD有向线段AB、CD是不同的。向量AB、CD是同一个向量。说明2：\n2021/8/91、零向量2、单位向量单位向量大小为1，方向不一定相同。所以0向量只有一个，而单位向量可以有无数个0向量大小为0，方向不确定的。可以是任意方向：长度为0的向量。记作0：长度为1个单位长度的向量。说明3：两个特殊向量思考：平面直角坐标系内，起点在原点的单位向量，它们的终点的轨迹是什么图形？\n2021/8/9三：向量之间的关系3.平行向量的定义：方向相同或相反的非零向量叫做平行向量我们规定零向量与任一向量平行两向量的平行与平面几何里两线段的平行有什么区别？\n2021/8/94.相等向量的定义：长度相等且方向相同的向量相反向量的定义：三：向量之间的关系ABDC\n2021/8/9任意一组平行向量都可以平移到同一直线上三：向量之间的关系5.共线向量与平行向量的关系：平行向量就是共线向量两向量的共线与平面几何里两线段的共线是否一样？为什么？说明：在平行向量、共线向量、相等向量的概念中应注意零向量的特殊性\n2021/8/9例1：已知O为正六边形ABCDEF的中心，在图中所标出的向量中：解：DOAFEBC\n2021/8/9AB分别以图中的格点为起点和终点作向量，例2：在图中的4×5方格纸中有一个向量（1）其中与相等的向量有多少个？（2）与长度相等的共线向量有多少个？\n2021/8/9合作探究：共有2种不同的模共有8种不同的向量\n2021/8/9若改为1×2的方格纸中的格点为起点和终点的所有向量中，可得到多少种不同的模？多少种不同的向量呢？变式训练共有4种不同的模共有14种不同的向量\n2021/8/9★题：★★★题：123456789101112★★题：欢迎来到：过关竞技场\n2021/8/9练习：1、单位向量是否一定相等？2、单位向量的大小是否一定相等？BACK不一定一定\n2021/8/9练习：1、平行向量是否一定方向相同？2、不相等的向量一定不平行吗？BACK不一定不一定\n2021/8/9BACK练习1、与零向量相等的向量一定是什么向量？2、与任意向量都平行的向量是什么向量？零向量零向量\n2021/8/9BACK练习1、若两个向量在同一直线上，则这两个向量是什么向量？2、共线向量一定在一条直线上吗？共线向量或者说平行向量不一定\n2021/8/9BACK练习：在质量、重力、速度、加速度、身高、面积、体积这些量中，哪些是数量？哪些是向量？数量有：质量、身高、面积、体积向量有：重力、速度、加速度\n2021/8/9在下列结论中，哪些是正确的？（1）如果两个向量相等，那么它们的起点和终点分别重合；（2）模相等的两个平行向量是相等的向量；（3）如果两个向量是单位向量，那么它们相等；（4）两个相等向量的模相等。正确的有：（4）\n2021/8/9练习:1.设O为正△ABC的中心,则向量AO,BO,CO是()A.相等向量B.模相等的向量C.共线向量D.共起点的向量BABCO\n2021/8/9BACK练习:命题：“│a│=│b│”成立，则“a=b”一定成立×\n2021/8/9BACK练习：1.已知a、b为不共线的非零向量,且存在向量c,使c∥a,c∥b,则c=____0\n2021/8/9BACK练习：1.与非零向量a平行的向量中，不相等的单位向量有_____个.2\n2021/8/9练习：如图,EF是△ABC的中位线,AD是BC边上的中线,在以A、B、C、D、E、F为端点的有向线段表示的向量中请分别写出（1）与向量CD共线的向量有___个,分别是______________________；（2）与向量DF的模一定相等的向量有__个,分别是_________________；（3）与向量DE相等的向量有__个,分别是___________。ABCDEFBACK7DC,DB,BD,FE,EF,CB,BC5FD,EB,BE,EA,AE2CF,FA\n2021/8/9如图,D、E、F分别是△ABC各边上的中点，四边形BCMF是平行四边形，请分别写出：（1）与ED相等的向量；（2）与ED共线的向量；（3）与FE相等的向量；（4）与FE共线的向量。ABCDFEMBACK(1)3个(2)9个(3)3个(4)11个\n2021/8/9课堂小结\n2021/8/9向量最初被应用于物理学，被称为矢量．很多物理量，如力、速度、位移、电场强度、磁场强度等都是向量。大约公元前３５０年，古希腊著名学者亚里士多德就知道了力可以表示为向量．向量一词来自力学、解析几何中的有向线段。最先使用有向线段表示向量的是英国大科学家牛顿。课堂小结向量及向量符号的由来\n2021/8/9空间向量及其运算\n2021/8/9复习回顾：平面向量1、定义：既有大小又有方向的量。几何表示法:用有向线段表示字母表示法：用小写字母表示，或者用表示向量的有向线段的起点和终点字母表示。相等向量：长度相等且方向相同的向量ABCD\n2021/8/92、平面向量的加法、减法与数乘运算向量加法的三角形法则ab向量加法的平行四边形法则ba向量减法的三角形法则aba－ba＋ba(k>0)ka(k<0)k向量的数乘a\n2021/8/93、平面向量的加法、减法与数乘运算律加法交换律：加法结合律：数乘分配律：\n2021/8/9推广:（1）首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量；（2）首尾相接的若干向量若构成一个封闭图形，则它们的和为零向量。\n2021/8/9正东正北向上F3F3=15N已知F1=10N,F2=15N，F1F2这三个力两两之间的夹角都为90度,它们的合力的大小为多少N?这需要进一步来认识空间中的向量\n2021/8/9起点终点\n2021/8/9平面向量概念加法减法数乘运算运算律定义表示法相等向量减法:三角形法则加法:三角形法则或平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律\n2021/8/9ABCDABCDABCDABCDA1B1C1D1CABDba\n2021/8/9平面向量概念加法减法数乘运算运算律定义表示法相等向量减法:三角形法则加法:三角形法则或平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律\n2021/8/9ababab+OAbBCa(k>0)ka(k<0)k空间向量的数乘空间向量的加减法\n2021/8/9ababOABb结论：空间任意两个向量都是共面向量，所以它们可用同一平面内的两条有向线段表示。因此凡是涉及空间任意两个向量的问题，平面向量中有关结论仍适用于它们。思考：它们确定的平面是否唯一？思考：空间任意两个向量是否可能异面？\n2021/8/9平面向量概念加法减法数乘运算运算律定义表示法相等向量减法:三角形法则加法:三角形法则或平行四边形法则空间向量及其加减与数乘运算空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律加法交换律数乘分配律加法:三角形法则或平行四边形法则减法:三角形法则数乘:ka,k为正数,负数,零加法结合律成立吗？\n2021/8/9abcOBCab+abcOBCbc+(平面向量)向量加法结合律在空间中仍成立吗?ab+c+()ab+c+()AA(a+b)+c=a+(b+c)\n2021/8/9abcOABCab+abcOABCbc+(空间向量)ab+c+()ab+c+()(a+b)+c=a+(b+c)向量加法结合律：空间中\n2021/8/9推广:（1）首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量；（2）首尾相接的若干向量若构成一个封闭图形，则它们的和为零向量。\n2021/8/9平面向量概念加法减法数乘运算运算律定义表示法相等向量减法:三角形法则加法:三角形法则或平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律小结加法交换律数乘分配律加法结合律类比思想数形结合思想数乘:ka,k为正数,负数,零\n2021/8/9例如:定义:我们知道平面向量还有数乘运算.类似地,同样可以定义空间向量的数乘运算,其运算律是否也与平面向量完全相同呢?\n2021/8/9显然,空间向量的数乘运算满足分配律及结合律\n2021/8/9\n2021/8/9例1：已知平行六面体ABCD-A1B1C1D1，化简下列向量表达式，并标出化简结果的向量。(如图)ABCDA1B1C1D1\n2021/8/9ABCDABCDA1B1C1D1ABCDa平行六面体：平行四边形ABCD平移向量到A1B1C1D1的轨迹所形成的几何体.a记做ABCD-A1B1C1D1\n2021/8/9例1：已知平行六面体ABCD-A1B1C1D1，化简下列向量表达式，并标出化简结果的向量。(如图)ABCDA1B1C1D1GM始点相同的三个不共面向量之和，等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量\n2021/8/9F1F2F1=10NF2=15NF3=15NF3\n2021/8/9例2：已知平行六面体ABCD-A1B1C1D1，求满足下列各式的x的值。ABCDA1B1C1D1\n2021/8/9例2：已知平行六面体ABCD-A1B1C1D1，求满足下列各式的x的值。ABCDA1B1C1D1\n2021/8/9例2：已知平行六面体ABCD-A1B1C1D1，求满足下列各式的x的值。ABCDA1B1C1D1\n2021/8/9例2：已知平行六面体ABCD-A1B1C1D1，求满足下列各式的x的值。ABCDA1B1C1D1\n2021/8/9ABMCGD练习1在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简\n2021/8/9ABMCGD(2)原式练习1在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简\n2021/8/9ABCDDCBA练习2在立方体AC1中,点E是面AC’的中心,求下列各式中的x,y.E\n2021/8/9ABCDDCBA练习2E在立方体AC1中,点E是面AC’的中心,求下列各式中的x,y.\n2021/8/9ABCDDCBA练习2E在立方体AC1中,点E是面AC’的中心,求下列各式中的x,y.\n2021/8/9作业AMCGDB\n2021/8/9再见谢谢大家的合作