高中数学导数的综合应用课件 49页

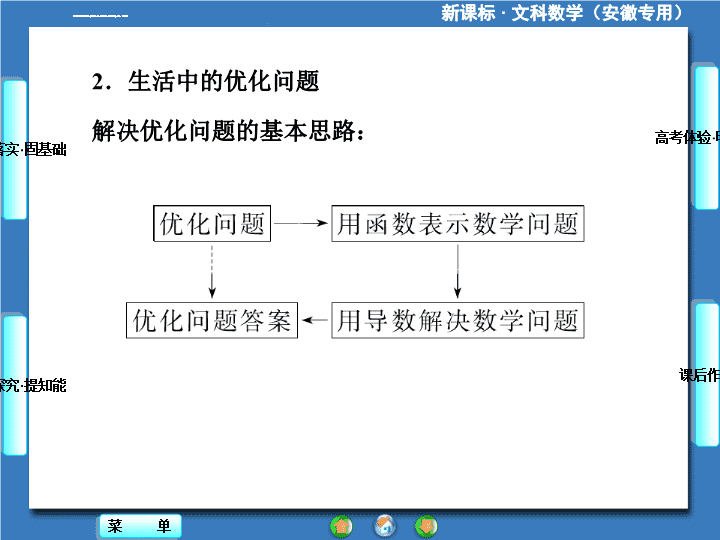
1．通常求利润最大、用料最省、效率最高等问题称为__________问题，一般地，对于实际问题，若函数在给定的定义域内只有一个极值点，那么该点也是最值点．优化\n2．生活中的优化问题解决优化问题的基本思路：\n1．函数的极大值一定比极小值大吗？【提示】极值是一个局部概念，极值的大小关系是不确定的，即极大值不一定比极小值大，极小值也不一定比极大值小．\n2．如何求实际问题中的最值问题？【提示】有关函数最大值、最小值的实际问题，一般指的是单峰函数，也就是说在实际问题中，如果遇到函数在区间内只有一个极值点，那么不与区间端点比较，就可以知道这个极值点就是最大(小)值点．\n【解析】∵f′(x)＝3ax2＋1，依题意f′(x)＝3ax2＋1有两个实根，∴a＜0.【答案】D\n【解析】y′＝－x2＋81(x＞0)，令y′＝0，即－x2＋81＝0得x＝9，当x∈(0，9)时，y′＞0，当x∈(9，＋∞)时，y′＜0.∴函数在(0，9)上单调递增，在(9，＋∞)上单调递减，∴当x＝9时，函数取得最大值，故选C.【答案】C\n\n【解析】由y＝f′(x)的图象知，函数f(x)在(－∞，0)上单调递增，在(0，＋∞)上单调递减，且f(－2)＝1，f(3)＝1，则不等式f(x2－6)＞1可转化为－2＜x2－6＜3，解得：2＜x＜3或－3＜x＜－2，故选A.【答案】A\n4．已知f(x)＝1＋x－sinx，试比较f(2)，f(3)，f(π)的大小为________．【解析】f′(x)＝1－cosx，当x∈(0，π]时，f′(x)＞0.∴f(x)在(0，π]上是增函数，∴f(π)＞f(3)＞f(2)．【答案】f(π)＞f(3)＞f(2)\n5．(2013·大连模拟)已知函数f(x)＝ex－2x＋a有零点，则a的取值范围是________．【解析】函数f(x)＝ex－2x＋a有零点，即方程ex－2x＋a＝0有实根，即函数g(x)＝2x－ex，y＝a有交点，而g′(x)＝2－ex，易知函数g(x)＝2x－ex在(－∞，ln2)上递增，在(ln2，＋∞)上递减，因而g(x)＝2x－ex的值域为(－∞，2ln2－2]，所以要使函数g(x)＝2x－ex，y＝a有交点，只需a≤2ln2－2即可．【答案】(－∞，2ln2－2]\n(2013·海淀模拟)已知函数f(x)＝ex(x2＋ax－a)，其中a是常数．(1)当a＝1时，求曲线y＝f(x)在点(1，f(1))处的切线方程；(2)若存在实数k，使得关于x的方程f(x)＝k在[0，＋∞)上有两个不相等的实数根，求k的取值范围．\n【思路点拨】(1)先求切点、切线斜率，再求切线方程；(2)利用导数判断函数f(x)在[0，＋∞)上的变化情况，数形结合求解．【尝试解答】(1)由f(x)＝ex(x2＋ax－a)可得f′(x)＝ex[x2＋(a＋2)x]．当a＝1时，f(1)＝e，f′(1)＝4e.所以曲线y＝f(x)在点(1，f(1))处的切线方程为y－e＝4e(x－1)，即y＝4ex－3e.\n(2)令f′(x)＝ex[x2＋(a＋2)x]＝0，解得x＝－(a＋2)或x＝0.当－(a＋2)≤0，即a≥－2时，在区间[0，＋∞)上，f′(x)≥0，所以f(x)是[0，＋∞)上的增函数，所以方程f(x)＝k在[0，＋∞)上不可能有两个不相等的实数根．当－(a＋2)＞0，即a＜－2时，f′(x)，f(x)随x的变化情况如下表：\n\n\n1．在解答本题(2)时应判断f(x)＞f(0)是否成立，这是容易忽视的地方．2．该类问题的求解，一般利用导数研究函数的单调性、极值等性质，并借助函数图象，根据零点或图象的交点情况，建立含参数的方程(或不等式)组求解，实现形与数的和谐统一．\n\n当x变化时，f′(x)与f(x)的变化情况如下表：\n\n\n(2013·大连模拟)设a为实数，函数f(x)＝ex－2x＋2a，x∈R.(1)求f(x)的单调区间与极值；(2)求证：当a＞ln2－1且x＞0时，ex＞x2－2ax＋1.【思路点拨】(1)令f′(x)＝0，求极值点，然后讨论在各个区间上的单调性．(2)构造函数g(x)＝ex－x2＋2ax－1(x∈R)，注意到g(0)＝0，只需证明g(x)在(0，＋∞)上是增函数，可利用导数求解．\n【尝试解答】(1)由f(x)＝ex－2x＋2a，x∈R，f′(x)＝ex－2，x∈R.令f′(x)＝0，得x＝ln2.于是当x变化时，f′(x)，f(x)的变化情况如下表：故f(x)的单调递减区间是(－∞，ln2)，单调递增区间是(ln2，＋∞)，f(x)在x＝ln2处取得极小值，极小值为f(ln2)＝eln2－2ln2＋2a＝2(1－ln2＋a)．\n(2)设g(x)＝ex－x2＋2ax－1，x∈R.于是g′(x)＝ex－2x＋2a，x∈R.由(1)知当a＞ln2－1时，g′(x)最小值为g′(ln2)＝2(1－ln2＋a)＞0.于是对任意x∈R，都有g′(x)＞0，所以g(x)在R内单调递增．于是当a＞ln2－1时，对任意x∈(0，＋∞)，都有g(x)＞g(0)．又g(0)＝0，从而对任意x∈(0，＋∞)，g(x)＞0.即ex－x2＋2ax－1＞0，故ex＞x2－2ax＋1.\n1．本题常见的错误有两点：(1)基础知识不过关，求错导数；(2)不等式证明思路不清晰，不会构造函数g(x)，发现不了g′(x)与f(x)的关系，导致不能运用第(1)问的结论．2．对于该类问题，可从不等式的结构特点出发，构造函数，借助导数确定函数的性质，借助单调性或最值实现转化．\n(2013·杭州模拟)设函数f(x)＝a2lnx－x2＋ax，a＞0.(1)求f(x)的单调区间；(2)求所有的实数a，使e－1≤f(x)≤e2对x∈[1，e]恒成立．(其中，e为自然对数的底数)．\n\n(2013·南京模拟)请你设计一个包装盒．如图2－12－2所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒．E、F在AB上，是被切去的一个等腰直角三角形斜边的两个端点．设AE＝FB＝x(cm)．\n(1)若广告商要求包装盒的侧面积S(cm2)最大，试问x应取何值？(2)某厂商要求包装盒的容积V(cm3)最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．【思路点拨】用x表示包装盒的高度和底面边长，则(1)包装盒的侧面积S是关于x的二次函数，可通过配方求最值；(2)包装盒的容积V是关于x的三次函数，可通过导数求最大值．\n\n利用导数解决生活中优化问题的一般步骤(1)分析实际问题中各量之间的关系，构造出实际问题的数学模型，写出实际问题中变量之间的函数关系y＝f(x)，并根据实际意义确定定义域；(2)求函数y＝f(x)的导数f′(x)，解方程f′(x)＝0得出定义域内的实根，确定极值点；(3)比较函数在区间端点和极值点处的函数值大小，获得所求的最大(小)值；(4)还原到实际问题中作答．\n\n\n\n把所求问题通过构造函数，转化为可用导数解决的问题，这是用导数解决问题时常用的方法．利用导数解决与方程、函数零点、不等式等问题时，常用到数形结合及转化与化归的数学思想．\n1.注意实际问题中函数定义域的确定．2．在实际问题中，如果函数在区间内只有一个极值点，那么只要根据实际意义判定是最大值还是最小值即可，不必再与端点的函数值比较．\n从近两年高考试题看，导数与方程、函数零点、不等式的交汇综合，以及利用导数研究生活中的优化问题，是考查的热点，并且常考常新．题型以解答题为主，综合考查学生分析问题、解决问题的能力．\n规范解答之三　构建函数模型证明不等式恒成立问题\n\n\n\n【解题程序】第一步：利用导数的几何意义求k的值；第二步：求f′(x)，构造函数h(x)；第三步：通过判断h(x)的正负，得到f′(x)的正负，从而求出单调区间；第四步：写出g(x)，判断h(x)在(0，＋∞)上的单调性；第五步：求出h(x)的最大值，从而得到欲证明的不等式．\n易错提示：(1)解答第(2)题时，因无法解方程f′(x)＝0，从而导致无法求解．(2)求解第(3)题时，因不会构造函数而导致解题失误．防范措施：(1)当方程f′(x)＝0无法用常规方法求解时，可用“试算”的方法寻找方程的根．(2)在用导数证明不等式时，若构造的函数比较复杂(求导后无法确定极值点)，可把函数写成两项积的形式(其中一个因式符号确定，另一个因式符号不定)，进而讨论符号不定的因式．\n1．(2012·福建高考)已知f(x)＝x3－6x2＋9x－abc，a0；②f(0)f(1)<0；③f(0)f(3)>0；④f(0)f(3)<0.其中正确结论的序号是(　　)A．①③　　　B．①④　　　C．②③　　　D．②④\n【解析】∵f′(x)＝3x2－12x＋9＝3(x－1)(x－3)，由f′(x)<0，得10，得x<1或x>3，∴f(x)在区间(1，3)上是减函数，在区间(－∞，1)，(3，＋∞)上是增函数．又a0，y极小值＝f(3)＝－abc<0，∴00.又x＝1，x＝3为函数f(x)的极值点，后一种情况不可能成立，如图．∴f(0)<0，∴f(0)f(1)<0，f(0)f(3)>0，∴正确结论的序号是②③.【答案】C\n\n\n课后作业（十五）\n